Размерная зависимость поверхностного натяжения наночастицы, находящейся в собственной матрице в изобарических условиях. 3. ОСНОВА. Нанотехнологии
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
Введение В настоящее время значительно возрос интерес к объектам нанометрового диапазона. По современным представлениям можно выделить два основных направления в изучении наночастиц: Изучение отдельных наночастиц. Основные усилия направлены на исследование физико-химических свойств частицы, полученных в результате диспергирования и агрегации атомов [1, 2]. Исследования наноструктурированных материалов. Такие материалы обычно состоят из большого числа наночастиц. Изменение свойств отдельных составных частей материала при переходе в область нанометровых размеров обуславливает появление новых свойств материала [3-5]. Слова с приставкой «нано» прочно вошли в обиход научной и научно-технической деятельности [6-9]. В американской литературе нанонауку определяют, как совокупность знаний о свойствах вещества в нанометровом масштабе, а нанотехнологию – как умение целенаправленно создавать объекты в размерах от 1 нм до 100 нм. Королевское общество Великобритании определяет нанотехнологию как создание, аттестацию, получение и применение структур, устройств и систем с контролируемыми размерами и формой нанометрового масштаба [10]. В отечественной литературе нанотехнологические термины определяются как: нанотехнологии – это технологии, направленные на создание и на практическое использование объектов и наносистем с заданными свойствами и характеристиками; нанообъект – определяется как вещество, материал, компонент, устройство или система с характерным размером, хотя бы в одном измерении в интервале от долей нанометра до 100 нм; наносистема – система, которая в качестве структурных элементов содержит нанообъекты, определяющие ее основные свойства и характеристики; наноструктурные материалы – это материалы, в которых основные структурные элементы (кристаллы, поры, слои и тд.) не превышают по размерам 100 нм, по крайне мере в одном напровлении. В последние десятилетия наиболее значительная часть экспериментов была проведена по синтезу и исследованию свойств наночастиц. Удалось разработать методы направленного регулирования размеров наночастиц. В настоящее время существуют методики, позволяющие выделять и стабилизировать отдельные наночастицы с изучением их физико-химических характеристик. Апробированы методики сортировки наночастиц по размерам, а также появилась возможность экспериментально изучить их строение, электронные и оптические и другие характеристики. Безусловно, уникальные свойства наночастиц позволяют рассматривать их как перспективные элементы устройств, которые найдут свое применение в наноэлектронике. Поверхностное натяжение входит во многие уравнения физики и определяет, в частности, капиллярное давление, краевой угол смачивания, давление насыщенного пара, скорость зародышеобразования, адсорбцию, емкость двойного электрического слоя, работу образования критических зародыша, длину капиллярных волн, и т.п. В последнее время с развитием физики и химии наноматериалов интерес к поверхностному натяжению значительно возрос [11]. При этом центральное место занимает вопрос о размерной зависимости поверхностного натяжения. В современной термодинамике поверхностных явлений применяются два основных метода рассмотрения межфазной границы. Первый из них, теория капиллярности Гиббса [12], базируется на таких понятиях, как разделяющая поверхность, идеализированная система сравнения и избыточные термодинамические величины. Этот метод не связан с каким-либо предположением относительно толщины межфазного слоя. Реальная двухфазная система в нем заменяется совокупностью двух фаз с четко обозначенной между ними геометрической поверхностью. Свойства фаз считаются одинаковыми до разделяющей поверхности (поверхность Гиббса), на которой все экстенсивные параметры меняются скачком. Второй метод [13-17] рассматривает поверхностный слой как самостоятельную фазу, имеющую конечную толщину и ограниченную двумя математическими поверхностями. В настоящее время наиболее полно изучена размерная зависимость поверхностного натяжения в изотермических условиях. Между тем, одним из интересных и важных вопросов физикохимии дисперсных систем является изучение зависимости температуры равновесия от радиуса. Фиксация температуры (T=const) при рассмотрении размерной зависимости поверхностного натяжения является существенным ограничением при построении теории дисперсных систем. В настоящей работе предпринята попытка установления зависимости поверхностного натяжения от радиуса в условиях, когда фиксируется давление в дисперсионной фазе. При этом в ходе рассмотрения размерной зависимости поверхностного натяжения наночастиц, учитывается изменения температуры равновесия с размером. Глава 1. Размерные эффекты в наносистемах Общее сведения по зависимости физических свойств от размера Многие науки занимаются взаимосвязью свойств материалов с характерными размерами их структурных элементов. Зависимость давления, насыщенного пара жидкости от кривизны капли, была предложена У. Томсоном (Кельвиным) еще в 1871 г. [18]. Экспериментально наблюдаемые высокие значения электросопротивления тонких пленок, превышающие электросопротивление крупнокристаллических металлических образцов, связывались с ограничением длины свободного пробега электронов размером образца. Размерный эффект - комплекс явлений, связанных с существенным изменением физико-химических свойств вещества вследствие [19]: - непосредственного уменьшения размера частица; - вклада границ раздела в свойства системы; - соизмеримости размера частиц с физическими параметрами, имеющими размерность длины и определяющими свойства системы. Размерные эффекты наблюдаются при уменьшении размера [20]: частиц, пленок и пор ниже некоторой пороговой величины. Такие эффекты появляются, когда средний размер кристаллических частиц не превышает 100 нм (рисунок 1), и наиболее отчетливо проявляются при размерах менее 10 нм [21].  Рисунок 1. Основные типы идеальных твердотельных Основные типы идеальных твердотельных наноструктур Квантовые размерные эффекты проявляются в электронных свойствах вещества или материала и связаны с уменьшением размерности электронного газа, что приводит к изменению энергетического спектра. Размерные эффекты можно условно разделить на два типа: Слабые эффекты, когда при увеличении удельной поверхности физико-химические свойства вещества меняются мало и все наблюдаемые изменения можно объяснить влиянием поверхности; Сильные эффекты, когда наблюдаемые кардинальные изменения свойств вещества невозможно интерпретировать как обычные поверхностные явления. Основной особенностью нанообъекта является то, что его структура и свойства зависят от геометрических параметров и числа атомов. При этом изменение размеров нанообъекта сопровождается изменением: энергетического состояния нанообъекта, как термодинамической системы; межатомных расстояний и взаимного расположения атомов в пространстве; электронной структуры; фононного и фотонного спектров; дефектной структуры; электрических, тепловых, магнитных свойств; химических свойств. С позиции квантовой механики электрон представлен волной, описываемой соответствующей волновой функцией. Распространение этой волны в наноразмерных твердотельных структурах контролируется эффектами, связанными с квантовым ограничением, интерференцией и возможностью туннелирования через потенциальные барьеры. Волновая функция дает статистическое описание электрона в пространстве [22]. Волна, соответствующая свободному электрону в твердом теле, может беспрепятственно распространяться в любом направлении. Электрон, попадая в твердотельную структуру, по крайней мере в одном направлении, ограничен и по своей величине сравним с длиной электронной волны. Колебания струны могут происходить только в режиме стоячих волн с длиной волны  . Данное поведение характерно для свободного электрона в твердотельной структуре, ограниченного размера или области твердого тела, ограниченной непроницаемыми потенциальными барьерами [23]. Аналогичные закономерности поведения характерны и для свободного электрона, находящегося в твердотельной структуре ограниченного размера или области твердого тела, ограниченной непроницаемыми потенциальными барьерами. На рисунке 2 такая ситуация проиллюстрирована на примере квантового шнура, у которого ограничены размеры сечения а и b. . Данное поведение характерно для свободного электрона в твердотельной структуре, ограниченного размера или области твердого тела, ограниченной непроницаемыми потенциальными барьерами [23]. Аналогичные закономерности поведения характерны и для свободного электрона, находящегося в твердотельной структуре ограниченного размера или области твердого тела, ограниченной непроницаемыми потенциальными барьерами. На рисунке 2 такая ситуация проиллюстрирована на примере квантового шнура, у которого ограничены размеры сечения а и b. Рисунок 2. Возможности для движения электронов в наноразмерной структуре В этих направлениях возможно распространение только волн с длиной, кратной геометрическим размерам структуры. Разрешенные значения волнового вектора для одного направления задаются соотношением к =2π/λп=nπ/L (п = 1, 2, 3,...), где L в соответствии с рисунком 2 может принимать значения, равные а или b. Для соответствующих им электронов это означает, что они могут иметь только определенные фиксированные значения энергии, т. е. имеет место дополнительное квантование энергетических уровней. Это явление получило название квантового ограничения. Вдоль же шнура могут двигаться электроны с любой энергией. Энергия электрона имеет дискретные значения - квантовые ограничения. Вдоль шнура могут двигаться электроны с любой энергией. Квантовое ограничение сопровождается как увеличением минимальной энергии запертого электрона, так и дополнительным квантованием энергетических уровней, соответствующих его возбужденному состоянию. Это приводит к различию электронных свойств наноразмерных структур от объемных свойств материала, из которого они сделаны.  Рисунок 3. Пространственное ограничение волновых функций в двумерных (2D), одномерных (1D) и нуль-мерных (0D) системах Уникальным свойством квантовых частиц и электронов, является способность проникать через преграду (рисунок 4) даже, когда энергия ниже потенциального барьера к данной преграде (туннелирование).  Рисунок 4. Туннелирование электрона с энергией E через потенциальный барьер высотой U, U > E Уникальным свойством квантовых частиц, в том числе и электронов, является их способность проникать через преграду даже в случаях, когда их энергия ниже потенциального барьера, соответствующего данной преграде. Это было названо туннелированием. Схематически оно представлено на рисунке 4. Будь электрон классической частицей, обладающей энергией E, он, встретив на своем пути преграду, требующую для преодоления большей энергииU, должен был бы отразиться от этой преграды. Квантовое ограничение, проявляясь в наноразмерных структурах, накладывает специфический отпечаток и на туннелирование. Так, квантование энергетических состояний электронов в очень тонких, периодически расположенных потенциальных ямах приводит к тому, что туннелирование через них приобретает резонансный характер, т.е. туннельно просочиться через такую структуру могут лишь электроны с определенной энергией. Квантование энергетических состояний электронов в очень тонких, потенциальных ямах приводит к тому, что туннельно пройти через такую структуру могут лишь электроны с определенной энергией. Размерно-зависимые свойства, наблюдающиеся у наноматериалов, представлены в таб.1. Таблица 1  Размерная зависимость физических свойств наноматериалов Размерная зависимость физических свойств наноматериалов
На температуру фазового превращения наночастицы влияет ее поверхностная энергия. Высокая поверхностная энергия в сочетании с малым размером зерна создают сжимающие напряжения в объеме зерна, что сдвигает фазовые равновесия в нанокристаллических материалах. Размерно–зависимые характеристики проявляются также в диэлектриках и магнетиках. Размерная зависимость свойств проявляется на таких характеристиках, как коэрцитивная сила, остаточная намагниченность, магнетосопротивление. При определенных размерах нанокластеров (1÷10 нм) проявляется явление супермагнетизма [24]. Важным фактором, определяющим механическое поведение наноматериаов, являются внутренние напряжения. Они всегда имеются в наноматериалах из-за большого числа близко расположенных границ зерен и тройных стыков зерен [25]. Внутренние напряжения могут возникать вследствие особенностей методов получения наноматериалов. Наличие высоких внутренних напряжений у нанокристаллов приводит также к изменению атомной структуры наноматериалов. Необычные физико-химические свойства наночастиц обусловлены тремя основными причинами. Во-первых, размер наночастиц сопоставим с Боровским радиусом экситонов в полупроводниках. Это определяет оптические, люминесцентные и редокс-свойства наночастиц. Во-вторых, для наночастиц доля атомов, оказавшихся на поверхности, составляет значительную часть от общего числа атомов наночастиц. Поверхностные атомы вносят большой вклад в термодинамические характеристики твердых тел и для наночастиц в значительной степени определяют структурные переходы и температуру плавления. В-третьих, собственный размер частиц сопоставим с размерами молекул. Это определяет специфику кинетики химических процессов на их поверхности [26]. Проблема размерных эффектов (т.е. влияние характерных размеров частиц, фазовых составляющих и тд.) охватывает практически все разновидности наноматериалов. Размерные эффекты давно изучаются в химии, физике и материаловедении. Формулы Лапласа (1.1.1), Томсона (1.1.2, 1.1.3), Толмена (1.1.4), Холла-Петча (1.1.6), Пинеса (1.1.8), Набарро-Херринга-Кобла (1.1.7) и Томпсона (1.1.5), отражающие влияние радиуса поры и частицы (r) на капиллярное давление (P), давление насыщенного пара (  ), растворимость ( ), растворимость ( ) и поверхностную энергию ( ) и поверхностную энергию (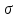 ), а также влияние размера зерна (L) на твердость, скорость ползучести ( ), а также влияние размера зерна (L) на твердость, скорость ползучести ( ), коэффициент вязкости ( ), коэффициент вязкости ( ) и влияние относительной толщины пленок (f) на проводимость ( ) и влияние относительной толщины пленок (f) на проводимость ( ) )        В формулах (1.1.1-1.1.8)  – атомный объем; подстрочный знак «0» относится к значениям – атомный объем; подстрочный знак «0» относится к значениям  и и  для плоских поверхностей и крупнозернистых образцов; k- постоянная Больцмана; для плоских поверхностей и крупнозернистых образцов; k- постоянная Больцмана; 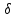 – константа Толмена; f=h/l (f<1); l – длина свободного пробега электрона; a – период решетки; в формуле (1.1.8) p=2 для случая диффузионной ползучести по Набарро-Херрингу, ap=3 – для диффузионной ползучести по Коблу; A – постоянная; D – коэффициент диффузии. – константа Толмена; f=h/l (f<1); l – длина свободного пробега электрона; a – период решетки; в формуле (1.1.8) p=2 для случая диффузионной ползучести по Набарро-Херрингу, ap=3 – для диффузионной ползучести по Коблу; A – постоянная; D – коэффициент диффузии. Роль размерных эффектов значительна в консолидированных наноматериалах, в которых нанозерна находятся в неизолированном или слабо скрепленном виде, а в консолидированном материале. Эти компакты (объемные консолидированные наноматериалы), пленки и покрытия получают методами порошковой и пленочной технологий, интенсивной пластической деформации, контролируемой кристаллизацией из аморфного состояния и другими способами. В таких (неполимерных) наноматериалах структура обычно рассматривается на основе извечтной классификации Г. Гляйтера, которая предусматривает четыре типа структур по химическому составу и распределению фаз, а также при разновидности по форме (таблица 2) Таблица 2 Классификация консолидированных наноматериалов по составу, распределению и форме структурных составляющих  С уменьшением размера структурных составляющих значительно возрастает роль поверхностей раздела (доля поверхностей раздела в общем объеме составляет  6b/L, где 2b – ширина границы, обычно применяется около 1 нм; при величине кристаллов 103 нм, 102 нм и 10 нм доля поверхностей раздела существенно возрастает – от 0,3 до 3 и 30%). 6b/L, где 2b – ширина границы, обычно применяется около 1 нм; при величине кристаллов 103 нм, 102 нм и 10 нм доля поверхностей раздела существенно возрастает – от 0,3 до 3 и 30%).Свойства поверхностей раздела в нанометровом интервале отличаются от таковых для крупнокристаллических объектов (для наноматериалов кроме обычных границ зерен надо принимать во внимание и возрастающее количество тройных стыков, а разнообразие поверхностей раздела в гибридных наноматериалах). С уменьшением кристаллов, частиц и т.д. из размер может стать соизмеримым с некоторым размерным параметром, характерным для некоторых физических явлений. Размерные эффекты в наноматериалах могут иметь квантовый характер, если, например, размер зерна становится соизмеримым с длиной волны де Бройля; квантовые размерные эффекты для металлических наноматериалов могут проявляться в свойствах, связанных, например с проводимостью лишь при размере кристаллов менее  1 нм; для полупроводников и для полуметаллов длина волны де Бройля значительно большем- около 100 нм. 1 нм; для полупроводников и для полуметаллов длина волны де Бройля значительно большем- около 100 нм.Дифференциальное уравнение Гиббса-Толмена-Кёнига-Баффа для зависимости поверхностного натяжения от размера в изотермических условиях Рассмотрим однокомпонентную систему, состоящую из дисперсной фазы () и дисперсионной среды () при постоянной температуре. В качестве дисперсной фазы будем иметь в виду сферическую частицу с радиусом r, расположенную на вогнутой стороне поверхности (внутренняя фаза). В качестве дисперсионной среды будем рассматривать массивную фазу (), расположенную на выпуклой стороне поверхности (внешняя фаза). В качестве разделяющей поверхности выберем поверхность натяжения, положение которой определяется условием [  ]=0. ]=0. При таком выборе, как известно, поверхностное натяжение равно работе образования единицы новой поверхности, и имеет место соотношение  где r– радиус поверхности натяжения, P – давление, - поверхностное натяжение. Поверхность натяжения делит объём поверхностного слоя  на две части: на две части:   Если поделить на число молей поверхностного слоя  выражение ( выражение ( ) можно записать в виде ) можно записать в виде Пользуясь условиями равновесия в рассматриваемой системе, получим   ( ( ) )где , S, - поверхность, энтропия и объём, приходящиеся на один моль Исключим из (  ), ( ), ( ), ( ), ( ) давление в фазах ) давление в фазах  и и  учтём, что Т=const. В результате получим учтём, что Т=const. В результате получим где  , ,  В случае сферической формы частицы можно получить   параметр (длина Толмена) параметр (длина Толмена)Введём безразмерную переменную  представим (1.2.6) в виде представим (1.2.6) в виде  Это дифференциальное уравнение является основным соотношением для искомой зависимости поверхностного натяжения от кривизны [27]. Это уравнение можно представить к виду  Решение уравнения Гиббса-Толмена-Кенига-Баффа при больших и предельно малых размерах наночастицы Дифференциальное уравнение (1.2.10) можно рассматривать в частных случаях, связанных с характерными размерами дисперсной частицы сферической формы, находящейся в дисперсной фазе (матрице). Для этой цели удобно воспользоваться соотношением (1.2.9). При очень больших размерах частицы в знаменателе второго члена в (1.2.9) можно пренебречь тремя последними, как величинами более высокого порядка малости по сравнению с первым членом (т.е. x3>>(2x2+2x+2/3)). В таком случае из (1.2.9) получаем  Откуда следует  или или  , где , где  , - поверхностное натяжение на плоской поверхности, для каждой х=0 или r=0. При таком условии размерные эффекты отсутствуют. Можно изменить характерный размер дисперсной частицы х=х* (или r=r*), при которых начинают проявляться наноразмерные эффекты. При этом можно завариться условием, при котором можно рассматривать как пороговое изменение поверхностного натяжения, каждое, из которых, можно зарегистрировать. , - поверхностное натяжение на плоской поверхности, для каждой х=0 или r=0. При таком условии размерные эффекты отсутствуют. Можно изменить характерный размер дисперсной частицы х=х* (или r=r*), при которых начинают проявляться наноразмерные эффекты. При этом можно завариться условием, при котором можно рассматривать как пороговое изменение поверхностного натяжения, каждое, из которых, можно зарегистрировать.Запишем (1.2.9) в виде  где  Заваримся условием  и тогда в скобке в знаменателе (1.2.12) можно пренебречь вторым слагаемым по сравнению с единицей ( и тогда в скобке в знаменателе (1.2.12) можно пренебречь вторым слагаемым по сравнению с единицей ( ). В таком случае полученный значения будут относиться к размерам х ). В таком случае полученный значения будут относиться к размерам х 2001 или r 2001 или r 2001 2001 при при  0,3 нм. Это соотношение значения радиуса частицы r=600,3 нм. Аналогичным результатом (начало проявления размерного эффекта) будем иметь место в областях x>201 (или r>>60,3 нм при 0,3 нм. Это соотношение значения радиуса частицы r=600,3 нм. Аналогичным результатом (начало проявления размерного эффекта) будем иметь место в областях x>201 (или r>>60,3 нм при  ) и x>201 (r ) и x>201 (r 30,3 нм при 30,3 нм при  ) при значениях ) при значениях  и и  . . Если принять условие  = (2х+2/3)(х3+2х2) = (2х+2/3)(х3+2х2) и пренебречь последними двумя слагаемыми в знаменателе (1.2.9) будем иметь и пренебречь последними двумя слагаемыми в знаменателе (1.2.9) будем иметь После интегрирования (1.3.3) получим уравнение  Каждое совпадает с уравнением Толмена [28]. Если условиями малости считать значения  , ,  и и  , то соответствующими областями применимости уравнения Толмена (1.2.14) будут соответственно x>13,3 (r>4 нм при , то соответствующими областями применимости уравнения Толмена (1.2.14) будут соответственно x>13,3 (r>4 нм при  ) и x ) и x . .Рассмотрим теперь предельно малые наночастицы, когда из размер сравним с размером кристаллического зародыша новой сферы. Это соответствует, когда можно пренебречь вторым членом в уравнении (1.2.9). Тогда будем иметь  Из которого, после интегрирования, получим  Также уравнение было получено Русановым А. И [29, 30]. Рассмотрим теперь ситуацию, когда в качестве дисперсной фазы () выступает фаза, у которой плотность меньше, чем плотность дисперсионной среды  . В этом случае, центр кривизны находится за пределами дисперсной фазы. Выберем в качестве разделяющей поверхности поверхность натяжения и введём в рассмотрение параметр Толмена. В рассматриваемом случае условие механического равновесия запишется в виде . В этом случае, центр кривизны находится за пределами дисперсной фазы. Выберем в качестве разделяющей поверхности поверхность натяжения и введём в рассмотрение параметр Толмена. В рассматриваемом случае условие механического равновесия запишется в виде (1.3.7) (1.3.7)Приведенные выше уравнения равновесия сохраняют силу, из чего следует решение  (1.3.8) (1.3.8)Данное уравнение (1.3.8) можно записать в виде  При очень малых значениях радиуса поверхности натяжения из (1.3.9) следует формула Русанова А.И. [31]  При достаточно больших размерах получим формулу Толмена для сферы относительной кривизны в виде  Расчёты показывают, что при одинаковых размерах дисперсной фазы значение поверхностного натяжения для одного и того же вещества на границе с отрицательной кривизной (пузырёк в жидкости или жидкая капля внутри твёрдого тела) больше, чем в случае положительной кривизны (жидкая капля в паре или твёрдая частичка в жидкости). Такой вывод был сделан ранее Русановым А.И. и он подтверждается в расчётах. Размерная зависимость поверхностного натяжения частиц произвольного размера в изотермических условиях Для получения точного уравнения, справедливого в изотермических условиях на всём интервале изменения радиуса поверхности натяжения (от 0 до ), воспользуемся следующим представлением функции F(x)  Проинтегрируем (  ) и ( ) и ( ) в левой части от ) в левой части от  до и в правой части от до x приводит к искомому выражению до и в правой части от до x приводит к искомому выражению  При переходе к переменной r это уравнение имеет вид  Из полученного выражения (1.4.3) следует, что 0 при r0. C увеличением r значения возрастают монотонно и при r имеем  В формуле (1.4.3) от специфики рассматриваемой (конкретной) системы зависят значения  и и 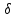 . Поэтому, кривая в безразмерных координатах . Поэтому, кривая в безразмерных координатах  носит универсальный характер и не зависит от конкретной природы дисперсной частицы () и дисперсионной среды (). Она универсальна и по границе раздела, т.е. относится к границам жидкость – пар, твёрдое – пар, твёрдое - жидкость. Отметим также, что эта кривая, справедлива для рассматриваемого случая положительной кривизны, подходит асимптотически снизу к единице ((r) стремится к носит универсальный характер и не зависит от конкретной природы дисперсной частицы () и дисперсионной среды (). Она универсальна и по границе раздела, т.е. относится к границам жидкость – пар, твёрдое – пар, твёрдое - жидкость. Отметим также, что эта кривая, справедлива для рассматриваемого случая положительной кривизны, подходит асимптотически снизу к единице ((r) стремится к  снизу). снизу).Для нахождения зависимости поверхностного натяжения от размера в случае отрицательной кривизны на всем интервале изменения размера проинтегрируем (1.3.10) слева от  до и справа от до и справа от  до х. В результате получим до х. В результате получим   Из Из  следует, что следует, что 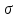 и r изменяются симбатно (т.е. и r изменяются симбатно (т.е.  ) и одновременно достигают нулевого значения ) и одновременно достигают нулевого значения  r=0. При приближении к значению r0=2,7995 r=0. При приближении к значению r0=2,7995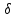 поверхностное натяжение поверхностное натяжение 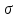 резко возрастает и стремится к бесконечности. При дальнейшем увеличении размера поверхностное натяжение резко уменьшается и затем монотонно приближается сверху к предельному значению резко возрастает и стремится к бесконечности. При дальнейшем увеличении размера поверхностное натяжение резко уменьшается и затем монотонно приближается сверху к предельному значению  на плоской поверхности. на плоской поверхности. Разновидности формулы Толмена по размерной зависимости поверхностного натяжения В литературе имеются достаточно много аналогичных выражений для зависимости поверхностного натяжения от размера, предложенные разными авторами в различное время [9, 13]. Анализ показывает, что многие из этих выражений являются равнозначными формулами Толмена. Так, достаточно часто встречается соотношение [27]  Можно показать, что (1.5.1) следует из (1.2.10), если воспользоваться разложением в ряд Тейлора по малому параметру y=8/r. Так, (1.5.1) можно привести к виду  При |y|<<1, разложим в ряд Тейлора по y=  правую часть (1.5.2) в нулевом приближении получаем правую часть (1.5.2) в нулевом приближении получаем После интегрирования  имеем имеем  . Если теперь экспоненты в . Если теперь экспоненты в  разложить в ряд по разложить в ряд по  с точностью с точностью  и и  будем иметь будем иметь  Выражение  предложено в работе [16], а предложено в работе [16], а  в работе [17]. в работе [17].Уравнение (1.5.1) можно представить в виде  Разложим экспоненту в (1.5.6) в ряд  до первого порядка, получаем до первого порядка, получаем  Данное уравнение  было предложено в работе [18]. было предложено в работе [18].Уравнение (1.5.1) можно также представить в виде   Разлогая экспоненту в  в ряд Тейлора по в ряд Тейлора по  до члена первого порядка получаем соотношение до члена первого порядка получаем соотношение  Каждое уравнение приведено в работе [19]. Аналогично проведем соотношение   Перечисление подобных примеров можно продолжить и дальше. Выводы к главе 1. Постановка задачи За последнее десятилетие во всем мире резко вырос интерес к поверхностным явлениям. Это, в первую очередь, связано с удивительными свойствами нанообъектов, в том числе наночастиц, нанопленок, нанопор, композиционных материалов, содержащих дисперсные частицы в нанометровом диапазоне. Многие специалисты считают, что прогресс в изучении и практическом использование наноматериалов определяется знаниями о поверхностных явлениях. Между тем, поверхностные свойства даже макроскопических тел недостаточно изучены к настоящему времени. Наиболее многочисленны соотношения по расчету поверхностного натяжения жидких (в основном бинарных) растворов на границе с паром. Так, в разное время предложены уравнения изотерм поверхностного натяжения, Жуковского, Батлера, Семенченко, Задумкина и др. Они получены, исходя их различных предпосылок в рамках тех или иных приближений. При этом, они как правило, содержат заранее неизвестные (трудно определенные) величины, среди которых параметры межчастичного взаимодействия в анизотропном поверхностном слое, состав и атомная структура поверхности, характеристики ближнего и дальнего порядка в поверхностном слое и другие. Более сложная ситуация имеет место при рассмотрении характеристик межфазного слоя в системах , содержащих наночастицы. При попытках описания зависимости поверхностных свойств наночастиц от основных параметров состояния в дисперсных системах, возникают значительные трудности. На данном этапе еще не развиты методы экспериментального измерения поверхностных характеристик наночастиц. Результаты по измерению поверхностного натяжения наночастиц по испарению малых частиц, изменению параметра решетки, понижению температуры плавления малых частиц и некоторыми другими методами, весьма малочисленны и носят одиночных характер. Значительные проблемы возникают при теоретическом описании поверхностных свойств в высокодисперсных системах. Дифференциальные уравнения для зависимости поверхностного натяжения от размера, полученые в рамках термодинамики дисперсных частиц, содержат величины, которые, в свою очередь, зависят от размера. При этом эти зависимости еще не установлены. Наиболее часто на практике используется формула Толмена, которая относятся к довольно большим размерам дисперсной частицы. Еще одна проблема принципиального характера, связана с тем, что попытки описания размерных эффектов относится, как правило, к изотермическим условиям. Так, дифференциальное уравнение Гиббса-Толмена-Кёнига-Баффа, следует из соотношений термодинамики дисперсных систем в изотермических условий (T=const). В связи с изложенным выше, в настоящей работе были поставлены следующие задачи: Получить в интегральной форме уравнение, для зависимости поверхностного натяжения дисперсной частицы сферической формы произвольного размера, находящейся в дисперсной среде (матрице), при условии постоянства давления во внешней фазе; Провести анализ нового уравнения изобары поверхностного натяжения и установить зависимости от размера поверхностного натяжения в случаях больших и предельно малых частиц; Провести расчет зависимости поверхностного натяжения от размера в изобарических условиях. |
