Подготовка к олимпиадам. Подготовка к олимпиадам через уроки занимательной математики
 Скачать 141.5 Kb. Скачать 141.5 Kb.
|
|
Подготовка к олимпиадам через уроки занимательной математики. Предмет математики настолько серьёзен, что нельзя упускать случая сделать его немного занимательным. Блез Паскаль Перед учителями, занимающимися с сильными школьниками, встаёт вопрос как подготовить школьников к олимпиадам или к «серьёзной» математике. Некоторые думают, что надо прорешивать задачи последних олимпиад, читать научную литературу, эти подходы недостаточно эффективны. Основу математического образования сильного ученика должно составлять решение и обсуждение задач, в процессе работы над которыми он знакомится с важными математическими идеями и теориями. Олимпиадных задач, очень много, большинство из них интересны школьнику, и среди них, много математически содержательных. Такие задачи могут составить основу изучаемого материала. Однако решение олимпиадных задач без изучения математических идей и теорий недостаточно эффективно даже для «чистой» подготовки к олимпиадам. Для успешного решения задач математических олимпиад высшего уровня необходимы в первую очередь общеукрепляющие средства: хорошая проработка алгебры ( культура алгебраических преобразований), проработка школьной геометрии. Задача этих олимпиад (кроме первых задач) практически всегда используют смешанный сценарий решения; редки задачи на применение некоторого метода или идеи в чистом виде. Решению таких «смешанных» задач должна предшествовать работа с ключевыми задачами, в которых идеи работают в чистом виде. Как удачно подобрать задачи для обучения учеников? Этот вопрос волнует всех учителей. Решать логические задачи очень увлекательно. В них вроде бы нет никакой математики - нет ни чисел, ни функций, ни треугольников, ни векторов, а есть только лжецы и мудрецы, истина и ложь. В то же время дух математики в них чувствуется ярче всего – половина решения любой математической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами. Логические или нечисловые задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определённом порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). К классу логических задач относятся также задачи на переливания и взвешивания (фальшивые монеты и т. п.) Известно несколько различных способов решения логических задач. Метод первый: Метод рассуждений Способ рассуждений – самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Пример: Задача: Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Решение. Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей. Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский. Метод второй: Метод таблиц Основной приём, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или её ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. Пример: Задача. Три клоуна Бим, Бам и Бом вышли на арену в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Бима цвета рубашки и туфель совпадали. У Бома ни туфли, ни рубашка не были красными. Бам был в зеленых туфлях, а в рубашке другого цвета. Как были одеты клоуны? Решение. Составим таблицу, в столбцах которой отметим возможные цвета рубашек и туфель клоунов (буквами К, З и С обозначены красный, зеленый и синий цвета). Будем заполнять таблицу, используя условия задачи. Туфли Бама зеленые, а рубашка не является зеленой. Ставим знак + в клетку 2-й строки и 5-го столбца, и знак - в клетку 2-й строки и 2-го столбца. Следовательно, у Бима и Бома туфли уже не могут быть зелеными, так же как не могут быть туфли Бама синими или красными. Отметим все это в таблице.
Далее, туфли и рубашка Бома не являются красными, отметим соответствующие ячейки таблицы знаком – . Из таблицы, заполненной на этом этапе, видим, что красные туфли могут быть только у Бима, а, следовательно, туфли Бома - синие. Правая часть таблицы заполнена, мы установили цвета обуви клоунов (табл.1). Цвет рубашки Бима совпадает с цветом его туфель и является красным. Теперь легко устанавливается владелец зеленой рубашки - Бом. Бам, в таком случае, одет в рубашку синего цвета.
Мы полностью заполнили таблицу, в которой однозначно устанавливаются цвета туфель и рубашек клоунов (см. табл. 2): Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета. Ответ: Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета. Метод третий: Метод блок – схем Этим методом решаются задачи, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости, а также задачи, связанные с операцией взвешивания на чашечных весах. Простейший приём решения задач этого класса состоит в переборе возможных вариантов. Этот метод решения не совсем удачный, в нём трудно выделить какой – либо общий подход к решению других задач. Более систематический подход к решению задач «на переливание» заключается в использовании блок – схем. Суть этого метода состоит в следующем. Сначала выделяются операции, которые позволяют нам точно отмерять жидкость. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в вилле схемы. Подобные схемы называются блок – схемами и широко используются в программировании. Составленная блок – схема является программой, выполнение которой может привести нас к решению поставленной задачи. Для этого достаточно отмечать, какие количества жидкости удаётся получить при работе составленной программы. При этом обычно заполняют отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся сосудов. Пример: Задача 1. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду. Решение. Перечислим все возможные операции, которые могут быть использованы нами, и введем для них следующие сокращенные обозначения: НБ — наполнить больший сосуд водой из-под крана; НМ — наполнить меньший сосуд водой из-под крана; ОБ — опорожнить больший сосуд, вылив воду в раковину; ОМ — опорожнить меньший сосуд, вылив воду в раковину; Б→М — перелить из большего в меньший, пока больший сосуд не опустеет или меньший сосуд не наполнится; М→Б — перелить из меньшего в больший, пока меньший сосуд не опустеет или больший сосуд не наполнится. Выделим среди перечисленных команд только три: НБ, Б→М, ОМ. Кроме этих трех команд рассмотрим еще две вспомогательные команды: Б = 0 ? — посмотреть, пуст ли больший сосуд; М = З ? — посмотреть, наполнен ли малый сосуд. В зависимости от результатов этого осмотра, мы переходим к выполнению следующей команды по одному из двух ключей - "да" или "нет". Такие команды в программировании принято называть командами "условного перехода" и изображать в блок-схемах в виде ромбика с двумя ключами-выходами. Договоримся теперь о последовательности выполнения выделенных команд. После Б→М будем выполнять ОМ всякий раз, как меньший сосуд оказывается наполненным, и НБ всякий раз, как больший сосуд будет опорожнен. Последовательность команд изобразим в виде блок-схемы (Рис. 1). Начнем выполнение программы. Будем фиксировать, как меняется количество воды в сосудах, если действовать по приведенной схеме. Результаты оформим в виде таблицы (табл.).
Дальше эта последовательность будет полностью повторяться. Из таблицы видим, что количество воды в обоих сосудах вместе образует следующую последовательность: 0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом, действуя по приведенной схеме, можно отмерить любое количество литров от 1 до 7. Чтобы отмерить еще и 8 литров, надо наполнить оба сосуда. Метод четвёртый: Метод математического бильярда Вам уже известна игра бильярд за прямоугольным столом с лузами. Появившись до нашей эры в Индии и Китае, бильярд через много веков перекочевал в европейские страны – упоминание о нём имеется в английских летописях VI века. В России бильярд стал известен и распространился при Петре I. Подобно тому, как азартная игра в кости вызвала к жизни «исчисление» вероятностей, игра в бильярд послужила предметом серьёзных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. Рассмотрим применение математического бильярда на примере решения задачи на переливание. Задачи на переливание жидкостей можно очень легко решать, вычёркивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма. Пример: Задача. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду. Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников (см.рис.1). 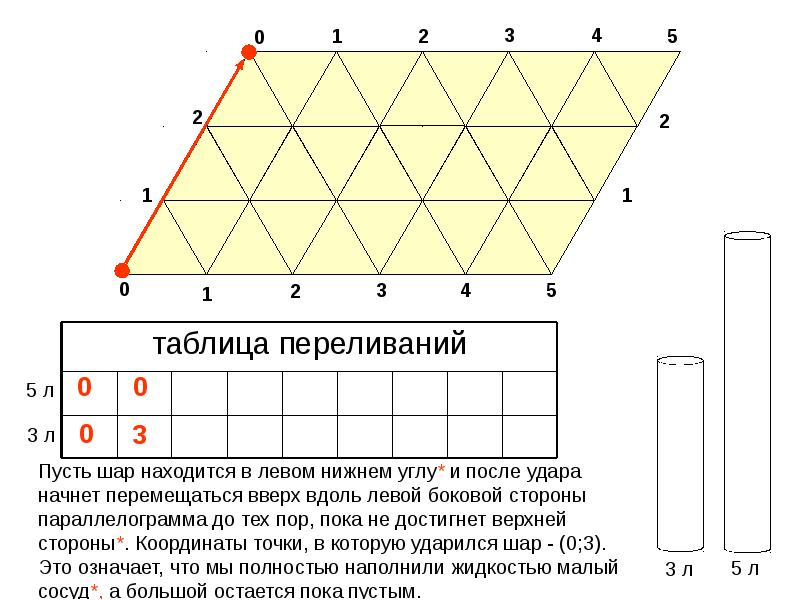 Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов. Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны в точке А. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке В, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд.
Прослеживая дальнейший путь шара, и записывая все этапы его движения в виде отдельной таблицы , в конце концов, мы попадаем в точку Н, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически в таблице. Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в пятилитровый сосуд. Если на диаграмме шар из точки О покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то получим более короткое решение задачи. Можно показать, что полученное решение с 6 переливаниями уже является самым коротким. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
