Математика. Понятие бесконечно малой, бесконечно большой функции Определение
 Скачать 69.03 Kb. Скачать 69.03 Kb.
|
|
Понятие бесконечно малой, бесконечно большой функции Определение: Функция альфа от х называется бесконечно малой, при х стремящемся к а (а- вещественное число или символ бесконечности), если для любого положительного числа эпсилон существует такая µа- окрестность точки а такая, что выполняется неравенство | |< Условие 1 эквивалентно следующему: , т.е. предел бесконечно мало альфа от х равен 0, и наоборот. Замечание: Если предел функции f(x) (при х-> a) равен А, то f(x) – А есть бесконечно малая, т.е. для функции f(x) имеющей предел А (при х-> a) существует представление в виде Опр. Функция f(x) называется бесконечно большой при (при х->a) (а- вещественное число или символ бесконечности), если Основные теоремы о бесконечно малых Все рассматриваемые функции определены на некотором множестве Х€R и х Теорема 1. Алгебраическая сумма конечного числа бесконечно малых при x->a функции есть бесконечно малая функция при х->a. В частности разность двух бесконечно малых при х->a функции есть бесконечно малая х->a функция Опр. Говорят, что f(x) ограничена х-> a если она ограниченная в некоторой µa-окрестности точки а. Теорема 2. Произведение ограниченной при х->a функции на бесконечно малую х->a функцию есть бесконечно малая функция при х->a. Теорема 3.Произведение конечно числа бесконечно малых при х->a функций есть бесконечно малая функция при х->a. Следствие из теоремы 3. Целая положительная степень бесконечно малой функции при х->a есть бесконечно малая функция при х->a. Замечание. Отношение двух бесконечно малых при х->a функций, может быть функцией произвольного поведения. Пример С помощью действия деления можно сравнивать между собой бесконечно малые. Опр. Две бесконечно малые альфа от х и бета от х при х-> a имеют одинаковый порядок при х->a, если их отношение имеет конечный предел, отличный от нуля(0) Опр. Говорят, что при х->a порядок бесконечно малой бета от х, выше порядка бесконечно малой альфа от х, если есть бесконечно малая функция при х->a, т.е. . В этом случае пишут, что Понятие дифференциала Пусть y=f(x) – некоторая дифференцируемая функция. Её приращение дельта y является важной характеристикой изменения этой функции на некотором заданном отрезке , но непосредственное вычисление приращения дельта y во многих случаях затруднительно, тогда поступают следующем образом -разбивают отрезок на конечное число достаточно малых отрезков и приближенно считают, что на каждом из них прирост функции происходит по закону прямой пропорциональности ( например, малый элемент кривой рассматриваем, как отрезок; неравномерное движение точки в течении малого промежутка времени рассматривают , как равномерное движение). Другими словами, предполагается, что на малом отрезке имеет место приближенное равенство , где к – коэффициент пропорциональности, который не зависит от дельта х, но возможно зависит от х. Если при этом окажется, что в принадлежащем подборе коэффициента к погрешность , будет бесконечно малой величиной высшего порядка относительно дельта х То величина, обозначаемая dy=k x называется дифференциалом функции y=f(x) в точки х. Из (1) следует равенство Очевидно, что слагаемое к х в формуле (2) является линейной частью приращения функции y. Его называют главной линейной частью Опр. Дифференциалом функции y=f(x) в точки х называется главная линейная относительно х часть приращения функции в этой точки. Теорема. (о единственности дифференциала): Функция может иметь только один дифференциал. Доказательство: Пусть f(x) имеет два дифференциала. По определению дифференциала имеем Перейдем к пределу при Связь дифференциала функции с производной. Дифференциал независимой переменной Теорема. Если функция имеет дифференциал, то эта функция имеет так же и производную. Доказательство: Пусть дана функция y=f(x) и пусть dy =к х – дифференциал этой функции по формуле (2) имеем Следствие: Дифференциал функции равен произведению производной этой функции на приращение независимой переменной Теорема. Если функция имеет производную, то эта функция имеет так же и дифференциал Доказательство: Пусть f(x) имеет производную Отсюда, Видно, что слагаемое представляет собой главную линейную часть приращения дельта у, т.е. является дифференциалом функции. Определение: Под дифференциалом независимой переменной понимают дифференциал функции тождественной с независимой переменной, т.е. dy=x. y=x у’=1 dx=дельта х, т.е. дифференциал независимой переменной равен приращению этой независимой переменной dy=y’dx Таким образом, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной. второе обозначение производной. Геометрический смысл дифференциала. Рассмотрим график функции y=f(x). Возьмем на графике функции точку М1 (x; у) М2 (х+  х; у+ х; у+ у). В точке М проведем касательную к этой функции. MKN – прямоугольный треугольник. у). В точке М проведем касательную к этой функции. MKN – прямоугольный треугольник.Из MKN: KN=MNtg =дельта x tg =y’ дельта x=dy Таким образом, имеем теорему: Дифференциал функции y=f(x) в данной точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получает приращение  х. х.Замечание: 1) если график функции выпуклый вниз, то  у> dy у> dy2) если график функции выпуклый вверх, то  y y Свойства дифференциала. df(x)=f’(x)dx Будем предполагать, что все рассматриваемые функции являются дифференцируемыми. Свойства: Дифференциал постоянной равен нулю. dC=C’dx=0 Дифференциал алгебраической суммы нескольких функций равен алгебраической сумме дифференциалов этих функций. d(u+v+w)=(u+v+w)’dx=(u’+v’+w’)dx= u’dx +v’dx +w’dx=du+dv+dw Если две функции различаются на постоянное слагаемое, то их дифференциалы равны. d(u+_C)= (u+_C)’dx=(u’+_C’)=u’dx+C’dx=du Постоянный множитель можно вынести за знак дифференциала. d(Cu)=(Cu)’dx=Cu’dx=Cdu Дифференциал произведения двух сомножителей равен произведению первого сомножителя на дифференциал второго + произведение второго сомножителя на дифференциал первого. d(uv)=(uv)’dx=(u’v+uv’)dx=vu’dx+uv’dx=vdu+udv Дифференциал частного равен дроби, числитель которой есть произведение знаменателя на дифференциал числителя минус произведение числителя на дифференциал знаменателя, а знаменатель есть квадрат знаменателя дроби. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента. y=f(g(x)), g(x)=u y=f(u) dy=df(u)=[f(u)]’dx=fu’ux’dx= fu’du Дифференциал высших порядков. Дифференциал df(x)=f’(x)dx называют дифференциалом 1-го порядка. Он является функцией аргумента х и дифференциала dx. Пусть функция f’(x) в свою очередь, дифференцируема в некоторой точке х. Будем рассматривать дифференциал dx как постоянный множитель и найдем d(df(x)). d(df(x))=d[f’(x)dx]=[f’(x)dx]’dx=f”(x)(dx)2 и так далее. Это выражение называется дифференциал 2-го порядка и обозначается d2f(x)(2-это не квадрат) dnf(x)=d(dn-1f(x))=f(n)(x)(dx)n - дифференциал n-го порядка. Формула Тейлора. Теорема(Тейлора): Пусть функция f(x) имеет в точке а и ее окрестности производные порядка n+1(Отсюда следует, что сама функция f(x) и ее производные до порядка n непрерывны и дифференцируемы в этой окрестности). Пусть х - любое значение аргумента из указанной окрестности, не совпадающая с точкой а Rn+1-остаточный член формулы Тейлора, записанный в формуле Лагранжа. Формулу Тейлора при а=0 называют формулой Макларена: - разложение функции в ряд по степеням х. Неопределенный интеграл. Понятие первообразной функции. Определение: Функция F(x) называется первообразной для функции f(x) на некотором промежутке Х, если х€Х выполняется равенство F’(x)=f(x). Задача дифференциального исчисления: По заданной первообразной F(x) найти её производную f(x). Задача интегрального исчисления: По заданной производной f(x) отыскать её первообразную F(x). Эта задача решается с помощью интегрирования. Это действие обратное и подобно большинству обратных действий многозначное, т.е. дающее для заданной производной f(x) не один результат F(x), а бесконечное множество первообразных. Убедимся в этом: Лемма: Если непрерывная функция имеет всюду на каком-либо отрезке производную равную нулю, то эта функция на данном отрезке есть постоянная величина. Док-во: Пусть f(x) непрерывна на [a, b] и пусть в каждой точке этого отрезка f’(x)=0. Для любых двух точек х1 и х2, принадлежащих отрезку [a, b] по теореме Лагранжа получим: f(x2)-f(x1) =f’( (кси))(x2-x1)=> f(x2)-f(x1)=0 => f(x2)=f(x1) Вывод: Так как х1 и х2 – произвольные точки, то полученное означает, что значения функции одинаковы во всех точках отрезка [a, b], f(x)=C, где С – некоторое число. Ч.Т.Д. Теорема: Если F(x) – первообразная для функции f(x) на промежутке Х, то любая другая первообразная для функции f(x) на том же промежутке может быть представлена в виде F(x)+c где С- произвольная постоянная. Доказательство. Пусть Ф(х) – любая другая первообразная для функции f(x) на промежутке X, то Ф`=f(x), тогда для любого аргумента x €Х найдём, [Ф(x)-F(x)]`=Ф`(x)-F(x)`=f(x)-f(x)=0 А по Лемме означает, что Ф(х)-F(x)=C Ф(х)=F(x)+C Вывод: Из доказанной теоремы следует, что множество функций F(x)+C, где F- одна из первообразных для F(x), а C произвольная константа, исчерпывает всё семейство первообразных для функции f(x). Определение: Если функция F(x)- первообразная для функции f(x) на промежутке X то множество функций F(x)+C называется неопределенным интегралом от функции f(x) на данном промежутке и обозначается символом  f(x)dx=F(x)+C f(x)dx=F(x)+Cf(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х - переменная интегрирования Основные свойства неопределенного интеграла: 1)Производная неопределенного интеграла равна подынтегральной функции; Дифференциал неопределенного интеграла равен подынтегральному выражению [  f(x)dx] `=[F(x)+C]`=F`(x)+C`=f(x) f(x)dx] `=[F(x)+C]`=F`(x)+C`=f(x)d[  f(x)dx] = [ f(x)dx] = [ f(x)dx] `dx=f(x)dx ЧТД f(x)dx] `dx=f(x)dx ЧТД2)Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной  dF(x)=F(x)+C dF(x)=F(x)+C3)Постоянный множитель можно вынести за знак неопределенного интеграла  Аf(x)dx=A Аf(x)dx=A f(x)dx, где A постоянная f(x)dx, где A постоянная4)Неопределенный интеграл под алгебраической суммой двух функций равен алгебраической сумме неопределённых интегралов слагаемых  Это свойство справедливо для любого конечного числа слагаемых Неопределенный интеграл Пусть функция y=f(x) определена на отрезке [a, b]. Разобьем отрезок [a,b] на n произвольных частей точками а=х0<х1 В каждом из полученных отрезков [xi-1, xi] выберем произвольную точку xi-1  i i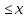 i. Через i. Через 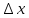 I обозначим разность xi - xi-1, которая называется длинной частичного отрезка [xi-1 , xi]. Составим сумму f( I обозначим разность xi - xi-1, которая называется длинной частичного отрезка [xi-1 , xi]. Составим сумму f( 1) : f( 1) : f( 1)* 1)*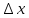 1+ f( 1+ f( 2)* 2)*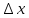 2+…+ f( 2+…+ f( i)* i)*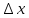 i+ f( i+ f( i)+…+f( i)+…+f( n)* n)*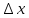 n= n=  i)* i)* 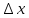 i (1) i (1)Эта сумма называется интегральной суммой для функции f(x) на отрезке [a,b] , соответствующей данному разбиению отрезка [a,b] на частичные отрезки и данному выбору промежуточных точек «  i». i».Геометрический смысл интегральной суммы Это сумма площадей S прямоугольников с основаниями 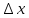 1, 1, 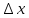 2 … 2 … 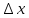 n и высотами f( n и высотами f( 1), f( 1), f( 2),… f( 2),… f( n). n). Обозначим через  длину наибольшего частичного отрезка длину наибольшего частичного отрезка 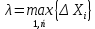 Определение: Если существует конечное предел интегральной суммы (1) при  ( ( ), то этот предел называют определенным интегралом от функции f(x) по отрезку [a, b] ), то этот предел называют определенным интегралом от функции f(x) по отрезку [a, b]  i= i= (2) (2)Функция f(x) – подынтегральная функция х – переменная интегрирования а – нижний предел интегрирования b - нижний редел интегрирования Свойства определенного интеграла Свойство определённого интеграла 1) а) Если пределы интегрирования совпадают, то определённый интеграл равен нулю  b) Если пределы интегрирования поменять местами то знак определенного интеграла сменится на противоположенный  2)Если отрезок интегрирования разбить на несколько других отрезков, то интеграл по всему отрезку будет равен сумме интегралов по всем его частям  3) Постоянный множитель можно вынести за знак определенного интеграла  4)Определенный интеграл от алгебраической суммы функций равен алгебраической сумме определенных интегралов слагаемых 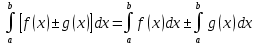 Это свойство можно распространить на любое конечное число слагаемых. 5)Теорема о среднем: Если функция f(x) непрерывна на отрезке [a, b] то на этом отрезке существует точка с такая что  Замечание (геометрический смысл теоремы о среднем): Величина определенного интеграла при f(x) ≥0 равна площади прямоугольника имеющего высоту f(c) и основание b-a Интеграл с переменным верхнем пределом Если изменять, например, верхней предел, так, чтобы не выходить из отрезка [a, b], то величина интегралов будет изменяться и будет представлять собой функцию своего верхнего предела  (а≤x≤b) Ф(х)= (а≤x≤b) Ф(х)= обозначим этот интеграл с переменным верхнем пределом через Ф(х) обозначим этот интеграл с переменным верхнем пределом через Ф(х)График: Теорема: Производная интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке равной верхнему пределу Ф`(х)= (  x = f(x) x = f(x) Формула Ньютона-Лейбница Из теоремы видно, что Ф(х) является первообразной для функции f(x). Пусть F(x) – любая другая первообразная для функции f(x) на отрезке [a, b]. Так как, первообразные Ф(х) и F(x) отличаются на постоянное слагаемое, то имеет место равенство Ф(х)= 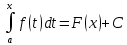 подставим в него: x=a подставим в него: x=aF(a)+C =0 => С = -F(a)  x=b  Разность F(b)-F(a), обозначает F(b)-f(a)=F(x) | ba  ab (3) ab (3)(3) – формула Ньютона-Лейбница Функции нескольких переменных Определение. Пусть X,Y,Z – некоторые числовые множества. Функцией двух переменных называется множество f, упорядоченных троек чисел (x,y,z) таких что, x€X, y€Y, z€Z и каждая упорядоченная пара чисел (x,y) входят в одну и только в одну тройку этого множества, а каждая z входит по крайне мере в одну тройку. При этом говорят, что упорядоченные пары чисел (x,y) поставлена в соответствии число z и пишут z=f(x,y). Число z называют значением функции в точке (x;y) переменную z называют зависимой переменной или функция a(x;y) не зависим или аргументы. Множество {(x,y)} – область определения функции, а Z – множество значений функций так как каждую упорядоченной паре (xy) в фиксированной прямоугольной системе координат соответствует единственная точка М и наоборот, то функцию двух переменных можно рассматривать как функцию точки М и вместо z=f(xy) пишем z=f(m). В этом случае областью определения функции является множество {М}. Пример: 1)z=x2+y2.Вся плоскость симметрии является областью определения функции. z=[0;+беск) 2)z=sqrt(1-x2-y2).Областью определения является круг с центром в начале координат с радиусом,равным 1. 1-x2-y2>=0 x2+y2<=1 z=[0;1] 3)z=1/sqrt(x2+y2-1).Областью определения является внешность круга с центром в начале координат с радиусом равным 1. x2+y2-1>0 x2+y2>1 z=(0;+беск). Из геометрии известно, что множество всех упорядоченных троек чисел (x,y,z) образует координатное пространство, при этом каждой тройке (x,y,z) в пространстве соответствует точка М(x0,y0,z0) и наоборот, тогда можно дать определение функции трех переменных U=f(M), где областью определения является все пространство или его часть и так далее. Предел функции двух переменных. Определение: Множество точек{M(x,y)}, координаты которых удовлетворяют неравенству sqrt((x-x0)2+(y-y0)2)<δ(дельта) или f(M,M0)< δ, называется δ-окрестностью точки M0(x0;y0). Другими словами δ-окрестность точки M0(x0;y0) – это все точки, лежащие внутри круга с центром в точке М радиуса δ. Рассмотрим последовательность точек M1(x1;y1), M2(x2;y2)….. Mn(xn;yn)….{Mn}. Определение: Последовательность точек {Mn} называется сходящейся в точке М0, если для любого малого числа ε>0, существует число N, такое что, n>N, выполняется неравенство ρ(Mn,M0)<ε(эпсилон). При этом называется пределом последовательности {Mn}. limMn=M0(при n стремится к бесконечности) Определение: Число А называется пределом функции z=f(M) в точке М0, если для любой сходящейся к М0 последовательности точек M1(x1;y1), M2(x2;y2)….. Mn(xn;yn)….Mn=М0 соответствующая последовательность значений функции f(M1),f(M2),….f(Mn)… сходится к числу А. Lim f(M)=A(при М стремящемся к М0) Lim f(x,y)=A(при х стремящемся к х0 и при у стремящемся к у0) Используя определение предела функции двух переменных можно перенести основные теоремы о пределах для функции одной переменной на случай функции двух переменных. Теорема: Пусть функции f(M) и g(M) определены на одном и том же {M} и имеют пределы в точке М0, равные В и С. Тогда функции f(M) ± g(M), f(M) х g(M) и f(M)/g(M) также имеют пределы в точке М0, равные соответственно В±С, ВхС, В/С, С≠0. Определение: z=f(M) называется бесконечно малой, при М стремящемся к М0, если lim f(M)=0. Функция z=f(M) называется непрерывной в точке М0, если предел функции в этой точке существует и равен значению функции в этой точке. Lim f(M)=f(M0)(при М стремящемся к М0) Lim f(x,y)=f(x0,y0)(при х стремящемся к х0 и при у стремящемся к у0) Назовем полное приращение z=f(M) в точке М0 функцию ∆z, определяемую формулой ∆z=f(M)-f(M0), где М – любая точка области определения функции. Обозначим через ∆х=х-х0 и ∆у=у-у0 , тогда в координатах ∆z будет иметь вид ∆z=f(x0+∆x,y0+∆y)-f(x0,y0). Определение: Функция, равная z=f(M) называется непрерывной в точке М0, если ее полное приращение в этой точке есть бесконечно малая функция, при М стремящемся к М0. Lim ∆z=0(при М стремящемся к М0) Определение: Множество точек плоскости называется связным, если две любые точки этого множества можно соединить непрерывной линией, состоящей из точек этого множества(является круг). Определение: Точка М называется внутренней точкой {M}, если существует δ-окрестность этой точки, состоящая из точек этого множества. Определение: Множество, состоящее только из внутренних точек, называется открытым множеством. Определение: Связное открытое множество называется открытой областью или просто областью. Примеры областей: внутренность треугольника, круга, эллипса. Определение: Множество точек, образованное областью и ее границей, называется замкнутой областью. Примеры: граница треугольника, круга, эллипса. Определение: Множество называется ограниченным, если существует круг, внутри которого оно содержится. Замкнутая ограниченная область, в которой определены функции двух переменных, является аналогом отрезка для функции одной переменной. Частная производная. Пусть функция z=f(M) определена в некоторой окрестности точки М(х,у). Предадим переменной х в точке М произвольное приращение ∆х, оставляя значение переменной у неизмененным, т.е. перейдем на плоскости от точки М(х,у) к точке М0(х+∆х,у), если при этом ∆х таково, что точка М лежит в указанной окрестности точки М, то соответствующее приращение функции будет иметь вид ∆xz=f(x+∆х,y)-f(x,y). Оно называется частным приращением функции по переменной х. Аналогично определяется частное приращение по переменной y: ∆y z=f(x,y+∆y)-f(x,y). Определение: Если существует предел lim ∆xz/∆x(lim ∆yz/∆y), то он называется частной производной функции z=f(M) в точке М по переменной х(у) Zx’= 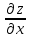 , zy’= , zy’= Вывод: Из определения следует, что частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной х при фиксированном значении переменной у. Вывод: Из определения следует, что частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной х при фиксированном значении переменной у.Понятие дифференцируемости двух переменных. Определение: Функция z=f(M) называется дифференцируемой в точке М, если ее полное приращение в этой точке может быть записано в виде ∆z=A∆x+B∆y+α(∆x,∆y)∆x+β(∆x,∆y)∆y(1), где А и В – некоторые независящие от ∆х и ∆у числа. α и β – бесконечно малые, при ∆х стремящемся к 0 и при ∆у стремящемся к 0 функции. Теорема: Если функция z=f(M) дифференцируема в точке М, то она непрерывна в этой точке. Доказательство: Если f(M) дифференцируема в точке М, то из соотношения (1) следует, что lim ∆z=0(при ∆х стремящемся к 0 и при ∆у стремящемся к 0), а это означает по определению, что функция непрерывна в точке М. Теорема(необходимое условие дифференцируемости): Если z=f(M) дифференцируема в точке М, то она имеет в этой точке частные производные fx’(x,y) и fy’(x,y) причем fх’(x,y)=А и fy’(x,y)=В. Доказательство: Так как функция f(M) дифференцируема в точке М, то имеет место соотношение (1). Положение в нем ∆у=0 ∆хz=A∆z+α(∆x,0)∆x Разделим это равенство на ∆х и перейдем к пределу при ∆х стремящемся к 0 Lim ∆xz/∆x=lim[A+α(∆x,0)]=A fx’(x,y)=A Следовательно, в точке М частная производная fx’(x,y)=A. Аналогично доказывается в точке М частная производная fy’(x,y)=B. Замечание: Утверждения, обратные доказанным теоремам, неверны, т.е. из непрерывности функции двух переменных в точке и существует и частные производные не следует дифференцируемость функции. Теорема(достаточное условие дифференцируемости): Если z=f(M) имеет частные производные в некоторой окрестности δ-окрестности в точке М и эти производные непрерывны в самой точке М, то функция дифференцируема а точке М. Следствие: Из непрерывности частных производных следует непрерывность самой функции. Дифференциал функции двух переменных. Определение: Дифференциалом функции dz, дифференцируемой в точке М функции z=f(M) называется главная линейная относительно приращений ∆х и ∆у часть полного приращения функции в точке М. dz=A∆x+B∆y A= fx’(x,y) B= fy’(x,y) ∆x=dx ∆y=dy dz=fx’(x,y)dx+fy’(x,y)dy Частные производные и дифференциалы высших порядков. Пусть fx’(x,y) и fy’(x,y) – частные производные определены в некоторой окрестности точки М и существуют в каждой точке этой окрестности. В этом случае частные производные представляют собой функции двух переменных х и у, определенно указанные в указанной окрестности точки М. Назовем их частными производными 1-го порядка. В свою очередь, частные производные по переменным х и у от функции fx’(x,y) и fy’(x,y) в точке М, если они существуют, называются частными производными 2-го порядка и обозначаются fxx’’(x,y)= 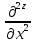 и fyy’’(x,y)= и fyy’’(x,y)= . Частные производные вида fxy’’(x,y) или fyx’’(x,y) называются смешанными частными производными. . Частные производные вида fxy’’(x,y) или fyx’’(x,y) называются смешанными частными производными.Смешанные частные производные обычно оказываются равными, но вообще говоря, смешанные частные производные зависят от порядка, в котором производится дифференцирование. Теорема: Если fxy’’(x,y) и fyx’’(x,y) существуют в некоторой δ-окрестности точки М(х,у) и непрерывны в самой точке М, то они равны между собой в этой точке, то есть имеет место равенство fxy’’(x,y)=fyx’’(x,y) Дифференциалы высших порядков. dz=fx’(x,y)+fy’(x,y) – дифференциал 1-го порядка функции z=f(x,y) Пусть функции fx’(x,y) и fy’(x,y) дифференцируемы в точке М. Будем рассматривать dx и dy как постоянные величины, тогда dz представляет собой функцию двух переменных х и у. Найдем d от dz: d(dz)=[fx’(x,y)dx+fy’(x,y)dy]x’dx+[fx’(x,y)dx+fy’(x,y)dy]y’dy= fxx’’(x,y)(dx)2+ fxy’’(x,y)dxdy+fyx’’(x,y)dydx+ fyy’’(x,y)(dy)2 Дифференциал d(dz) обозначают d2z и называют дифференциалом 2-го порядка функции z=f(x,y). Если смешанные частные производные равны, то d2z= fxx’’(x,y)(dx)2+ 2fxy’’(x,y)dxdy+fyy’’(x,y)(dy)2. Экстремумы функции двух переменных. Пусть функция z=f(x,y) определена в некоторой окрестности точки М0(х0,у0). Определение: Говорят, что функция z=f(x,y) имеет в точке М0 локальный максимум(минимум), если существует такая окрестность точки М0, в которой для любой точки М(х,у) выполняется неравенство f(x,y) Из определения следует, что если функция z=f(x,y) имеет экстремум в точке М0, то ее полное приращение ∆z=f(M)-f(M0)<0 max(>0 min) Верно обратное: если в некоторой окрестности точки М0 выполняется одно из неравенств ∆z)<0(>0), то функция имеет минимум(максимум) в точке М0. Теорема(необходимое условие экстремума функции двух переменных): Если функция f(x,y) имеет в точке М0 экстремум и имеет в точке М0 частные производные 1-го порядка, то в этой точке частные производные 1-го порядка равны 0. fx’(x0,y0)=fy’(x0,y0)=0 Доказательство: Докажем равенство нулю частная производная по х в точке М0. fx’(x0,y0)=0 Для этого рассмотрим в окрестности точки М0 только точки, для которых у=у0. Получена функция f(x,y0) одной переменной х, которая имеет в точке х=х0 экстремум и производную fx’(x0,y0), тогда по необходимому условию экстремума функции одной переменной, эта производная равна 0. Аналогично доказывается равенство нулю частной производной по у. Теорема(достаточное условие экстремума функции двух переменных): Пусть в точке М0 для возможного экстремума(то есть М0 – стационарная точка) и некоторой ее окрестности функция f(x,y) имеет непрерывные частные производные 2-го порядка. Обозначим через ∆=  , тогда 1)если ∆>0, то в точке М0 функция имеет экстремум, причем если fxx’’(x0,y0)<0, то это локальный максимум, и если fxx’’(x0,y0)>0, то это локальный минимум; 2)если ∆<0, то в точке М0 функция не имеет экстремума. Замечание: Если ∆=0, то функция в точке М0 может иметь экстремум, но может и не иметь его. Двойной интеграл. Определение двойного интеграла. Пусть в ограниченной замкнутой области S плоскости Оху задана непрерывная функция f(x,y). Разобьем область S на ячейки Si прямыми линиями, параллельными осям координат. В каждой ячейке Si возьмем точку (xi,yk) – нижняя левая вершина прямоугольника. Составим двумерную интегральную сумму. Обозначим через ∆xi=xi+1-xi ∆yk=yk+1-yk f(xi,yk)∆xi∆yk Определение: Двойным интегралом от непрерывной функции f(x,y), распространенным на ограниченную замкнутую область S плоскости Оху, называют предел соответствующей двумерной интегральной суммы. Lim f(xi,yk)∆xi∆yk= f(x,y)dxdy (1) Свойства двойного интеграла Так как основные свойства определенного интеграла можно вывести из определения интеграла как предела интегральной суммы, то эти свойства распространяются и на случай кратных интегралу. Если С – произвольное число, то: 1) 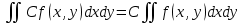 2) 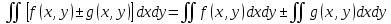 3) Если область S является объединением областей S1 и S2(S= S1  S2), не имеющих общих внутренних точек, то S2), не имеющих общих внутренних точек, то 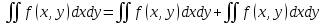 4) Теорема о среднем: Если функция  непрерывна в области S, то в этой области найдется такая точка ( непрерывна в области S, то в этой области найдется такая точка (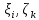 ), что ), что  ( (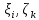 )s, где s – площадь области S. )s, где s – площадь области S.Расстановка пределов в двойном интеграле. Различают два вида области интегрирования. Область 1-го типа ограничена слева и справа прямыми х=х1,х=х2, а снизу и сверху – непрерывными кривыми у=φ1(х),у=φ2(х), каждая из которых пересекается с вертикалью х=Х(x1  , где при вычислении внутреннего переменная х полагается постоянной. , где при вычислении внутреннего переменная х полагается постоянной.Область 2-го типа ограничена снизу и сверху прямыми у=у1,у=у2, а слева и справа – непрерывными кривыми х= 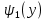 ,х= ,х= , где каждая из этих кривых пересекается с горизонталью у=У(y1 , где каждая из этих кривых пересекается с горизонталью у=У(y1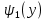 до до  . Аналогично предыдущему случаю имеем: . Аналогично предыдущему случаю имеем: , где при вычислении внутреннего интеграла переменная у считается постоянной. , где при вычислении внутреннего интеграла переменная у считается постоянной.Если область интегрирования не принадлежит к одному из рассмотренных типов, то ее разбивают на части, каждая из которых является областью типа 1 или типа 2. Геометрические приложения двойных интегралов. 1) Вычисление площадей плоских фигур. Площадь плоской области S вычисляется по формуле: S=  2) Вычисление объемов: Объем V цилиндроида, ограниченного сверху непрерывной поверхностью z=f(x,y), снизу плоскостью z=0(Оху), а с боков прямой цилиндрической поверхностью, вырезывающей на плоскости Оху область S равен: V=  Тройной интеграл. Определение тройного интеграла. Пусть f(x,y,z) – непрерывная функция, заданная в области V. Разобьем тело V на прямоугольные параллелепипеды с ребрами ∆хi;∆yj;∆zk плоскостями, параллельными координатным плоскостям. В каждом параллелепипеде возьмем точку с координатами (хi;yj;zk) и составим интегральную сумму: f(хi,yj,zk) ∆хi∆yj∆zk Определение: Тройным интегралом от функции f(х,y,z), распространенным на область V, называется предел соответствующей трехкратной интегральной суммы: Lim f(хi,yj,zk) ∆хi∆yj∆zk=  Вычисление тройного интеграла сводится к последовательному вычислению трех обыкновенных интегралов. Если область V ограничена следующими кривыми и поверхностями х=х1,х=х2(х2>x1),y=φ1(x),y=φ2(x),z=ψ1(x,y),z=ψ2(x,y), тогда  |
