Вар9. Построим графики линейных функций
 Скачать 120.77 Kb.
|
|
Вариант № 9 1.9. Построить на плоскости область решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значения функции    Построим графики линейных функций. 
Построим вектор целевой функции  с координатами (7;1). Решением для данной функции является перпендикуляр.Перемещая параллельно перпендикулярные прямые, получим, что максимальное значение достигается в точке А, а минимальное – в точке В. Найдем координаты этих точек.    - наибольшее значение   - наименьшее значениеОтвет:   .2.9. Предприятию необходимо перевезти со склада по железной дороге продукцию трех видов: продукции первого вида не более  изделий, продукции второго вида не более  изделий и продукции третьего вида не более  изделий. Для этой перевозки подразделение железной дороги может выделить специально оборудованные вагоны двух типов A и B. Для полной загрузки вагона в него следует помещать продукцию всех трех видов. При этом в вагоне типа А входят  изделий первого вида,  изделий второго вида и  изделий третьего вида. В вагон типа В входят  изделий первого вида,  изделий второго вида и  изделий третьего вида. Экономия от перевозки в вагоне типа А составляет  рублей, в вагоне типа В –  рублей.Сколько вагонов каждого типа следует выделить для этой перевозки, чтобы суммарная экономия от перевозки была максимальной? Найти решение двумя способами: геометрически и симплекс методом.    Составим систему уравнений.  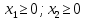  Построим графики линейных функций. 
Построим вектор функции  с координатами (6;2).Наибольшее значение достигается в точке А. Найдем координаты этой точки, составив систему уравнений.    Решение симплекс методом   
|
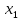
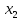
17,5
8
