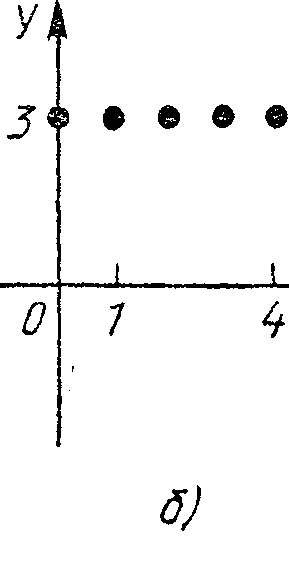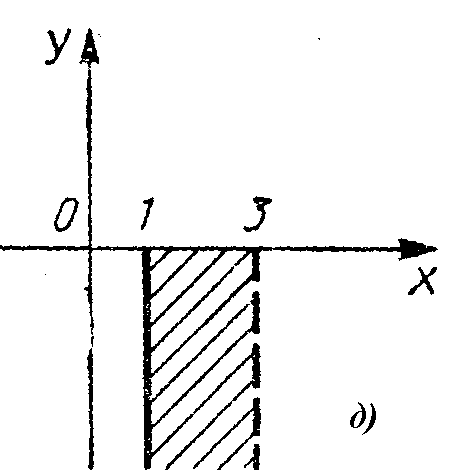Семестр 1. Практическое занятие 1.1. Множество. Способы задания множеств. Отношения между множествами.
Вопросы и задания для подготовки к занятию:
Приведите примеры множеств, включающих в себя однородные объекты. Например, мебель – это множество, которое включает в себя стул, стол, сервант и пр.
Запишите с помощью математических символов следующие предложения:
4 натуральное число;
2,1 не является целым числом;
множество В является подмножеством множества О;
множества К и С равны;
Задайте множества А и В другим способом, если А ={1, 2, 3, 4, 5, 6, 7,8}, В = {b, b N, b6}. Изобразите эти множества с помощью кругов Эйлера, каково отношение между этими множествами?
Сформулируйте определения понятий «характеристическое свойство множества», «равные множества», «подмножество».
Р – множество натуральных чисел, больших 7 и меньших 14. Выясните, какие из чисел 13, 10, 5, 7, 14 ему принадлежат, а какие не принадлежат. Запишите решение, используя математические символы.
А – множество решений уравнения  . Верно ли, что А – пустое множество? Приведите примеры уравнений, множество решений которых состоит из: . Верно ли, что А – пустое множество? Приведите примеры уравнений, множество решений которых состоит из:
одного элемента;
двух элементов;
трех элементов.
Запишите множество букв в слове «математика» и множество цифр в записи числа 515353.
Изобразите на координатной прямой множество Х, если:


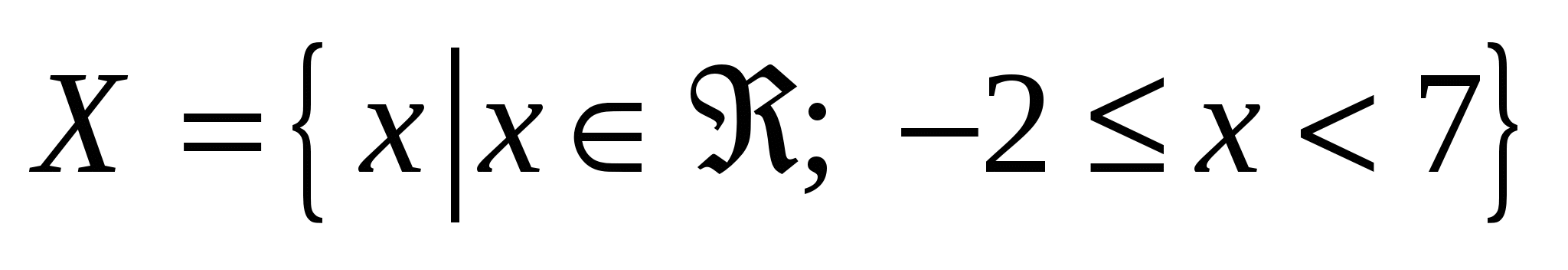 . .
Задайте двумя способами множество точек координатной прямой (рис. 1)
Задания для самостоятельной работы
Запишите множество А, элементами которого являются натуральные числа, меньшие 8, используя символические записи характеристического свойства и перечисления элементов множества. Верно, ли, что: а) 5 А; б) 0 А; б) 0  А; в) 8 А; в) 8 А? А?
Постройте прямую и отметьте на ней начало отсчета, единичный отрезок, точку А(5) и все точки, расстояние от которых от точки А: равно 2, не более 2.
Дано множество С = {213, 45, 324, 732, 136}. Составьте подмножества множества С, состоящие из чисел, которые:
делятся на 3;
не делятся на 4;
не делятся на 5.
А – множество натуральных чисел, меньших 20; В, С, Е, Н – подмножества множества А, такие, что В состоит из чисел, кратных 6, С – из чисел, кратных 2, Е – из чисел, кратных 3, Н – из чисел, кратных 2 и 3 одновременно. Перечислите элементы множеств А, В, С, Е, Н и укажите среди них равные множества.
О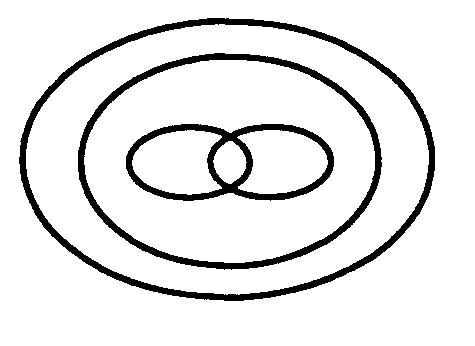 тношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств. тношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств.
Пусть разные строчные буквы обозначают разные предметы. Для каких из следующих пар множеств имеет место отношение А В или В А:
А={а, b, с, d}, В = {а, с, d};
А = {а, b}, В = {а, с, d};
А =, В = ;
А =, В = {а, b, с};
Какие из следующих пар множеств связаны между собой отношением включения:
А = {х х, х > 2}, В = {уу N, у > 2};
А ={х÷ хÎ R, х > 0}, В ={у÷у Î N, у > 0};
А ={х÷ хÎ N, х2 > 4}, В ={х÷ хÎN, х2 > 5};
А - множество многоугольников с периметром 4, В - множество квадратов с площадью 1?
Равны ли следующие множества: А = {2, 4, 6} и В = {6, 4, 2}; А = {1, 2, 3} и В ={I, II, III}; А = {{1, 2} {2, 3}} и В = {2, 3, 1};
Практическое занятие 1.2. Операции над множествами.
Вопросы и задания для подготовки к занятию:
Дайте определения понятиям «объединение множеств», «пересечение множеств». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.
Сформулируйте свойства операций объединение и пересечение множеств. Проиллюстрируйте их с помощью кругов Эйлера.
Дайте определения понятиям «разность множеств», «дополнение множества». Дайте этим операциям графическую иллюстрацию с помощью кругов Эйлера.
Сформулируйте свойства разности множеств.
Известно, что 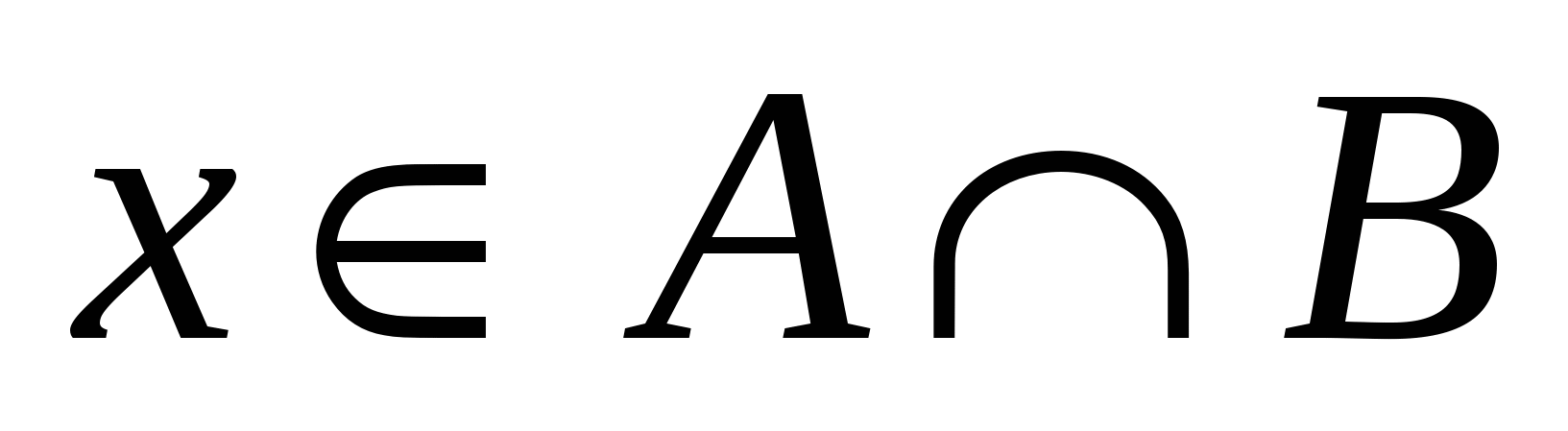 . Следует ли из этого, что: . Следует ли из этого, что:
Найдите пересечение, объединение, разность
[1; 5] и [3; 7];
А=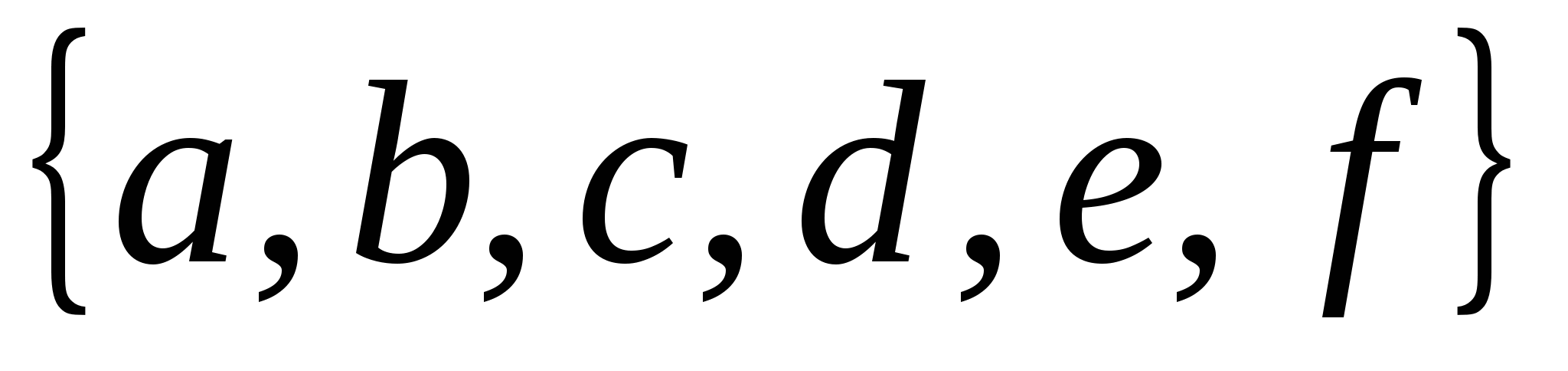 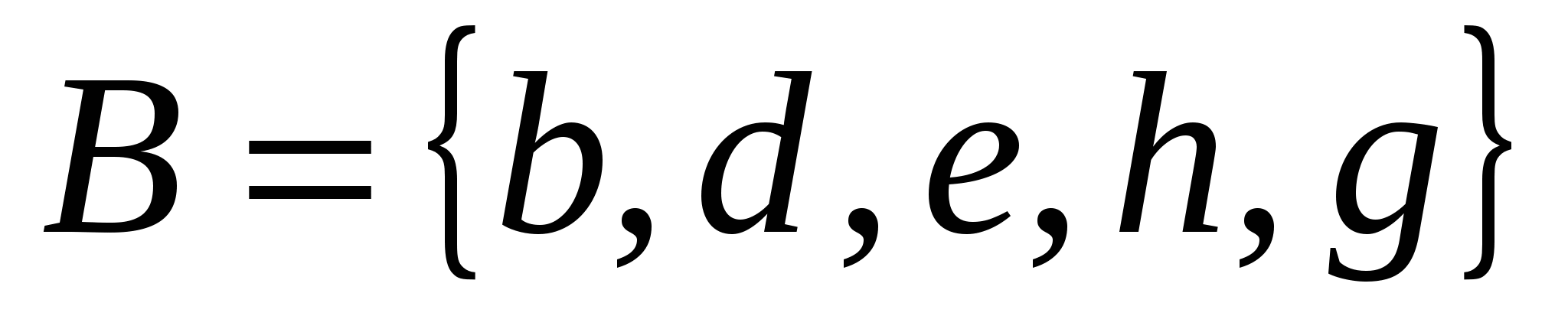 ; ;
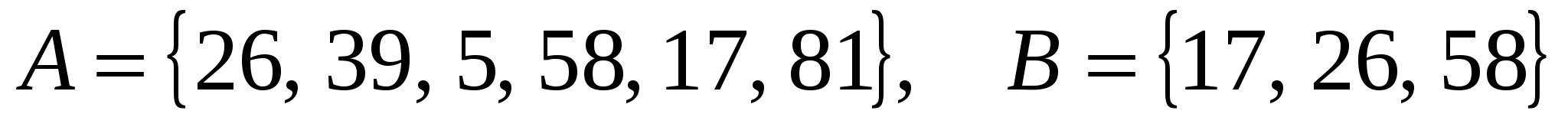 ; ;
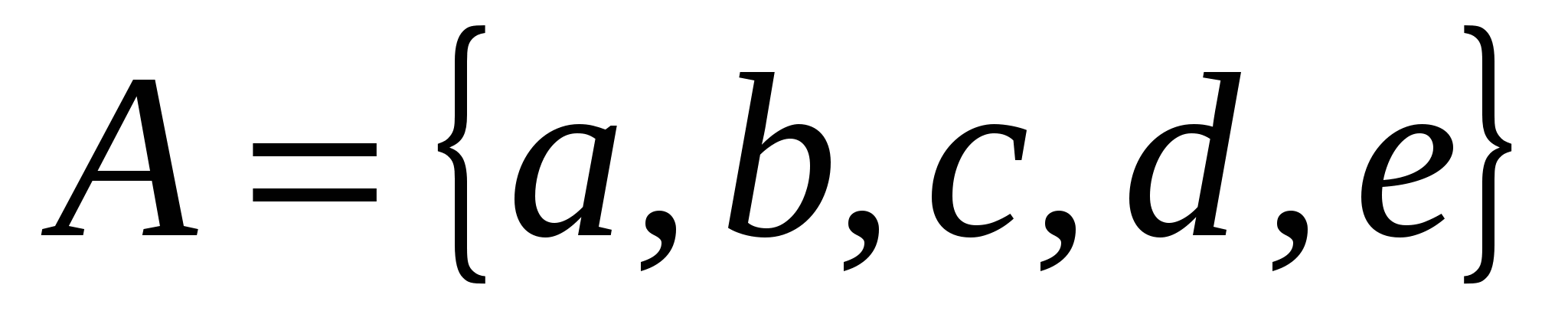 и и ; ;
; 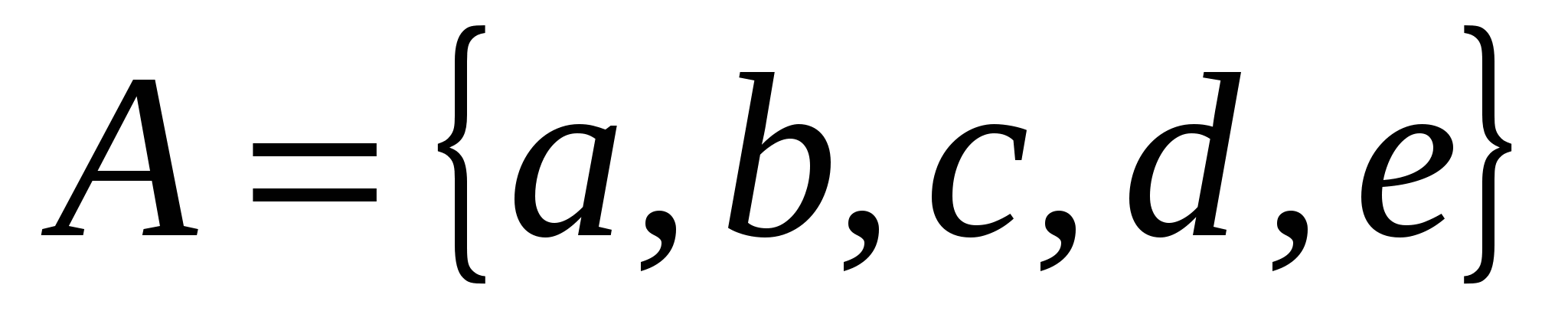 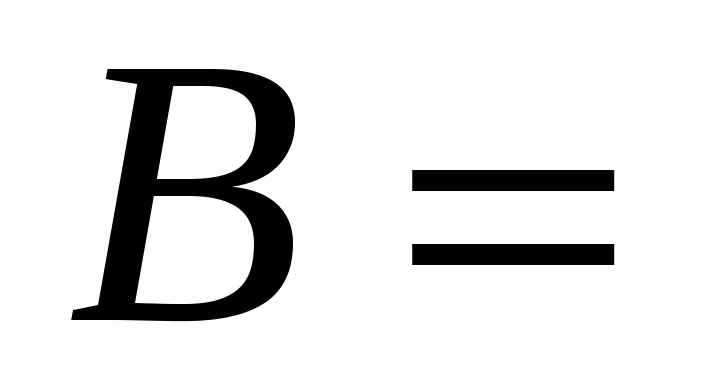 Ø.. Ø..
Известно, что  . Следует ли из этого, что: . Следует ли из этого, что:
Найдите разность числового отрезка [1; 5] и числового отрезка [3; 7].
Сформулируйте условия, при которых истинны следующие высказывания:
 ; ;
 . .
Задания для самостоятельной работы
Перечислите элементы, принадлежащие пересечению множества букв в слове «математика» и множества букв в слове «грамматика». Из каких элементов состоит объединение данных множеств?
Р – множество натуральных делителей числа 18, Н – множество натуральны делителей числа 24. укажите характеристическое свойство элементов пересечения множеств Р и Н и перечислите его элементы.
Найдите пересечение и объединение множеств К и М, если К – множество двузначных чисел, М – множество нечетных чисел. Верно ли, что: а) 21 ; б) ; б)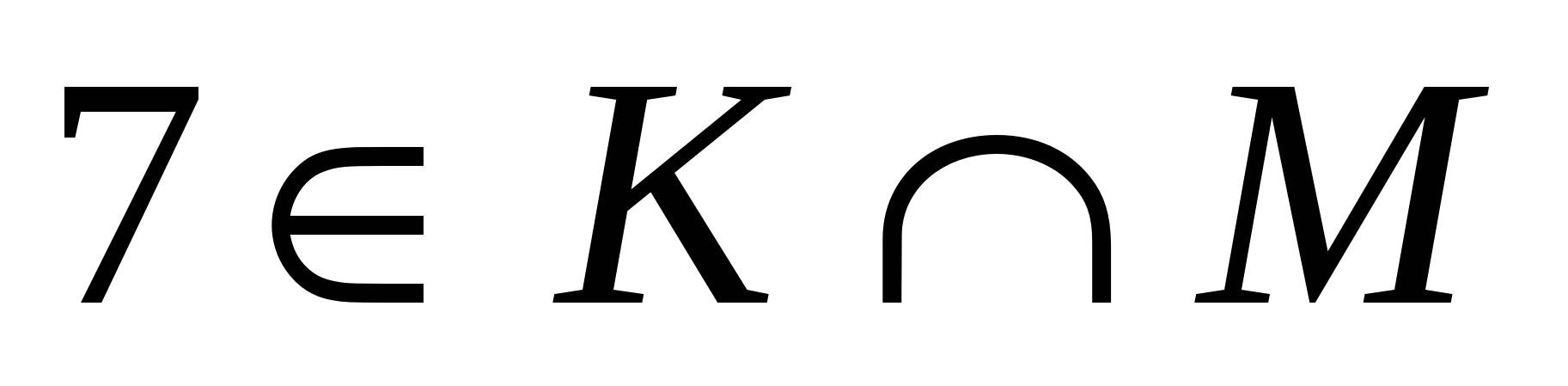 ; в) ; в) 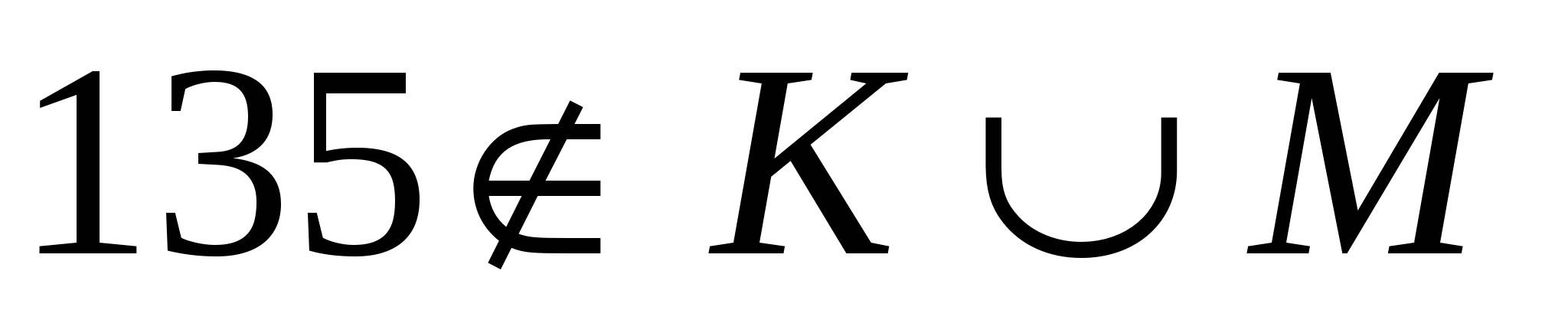 ; г) ; г)  . .
Н айти объединение и пересечение множеств А и В, если айти объединение и пересечение множеств А и В, если 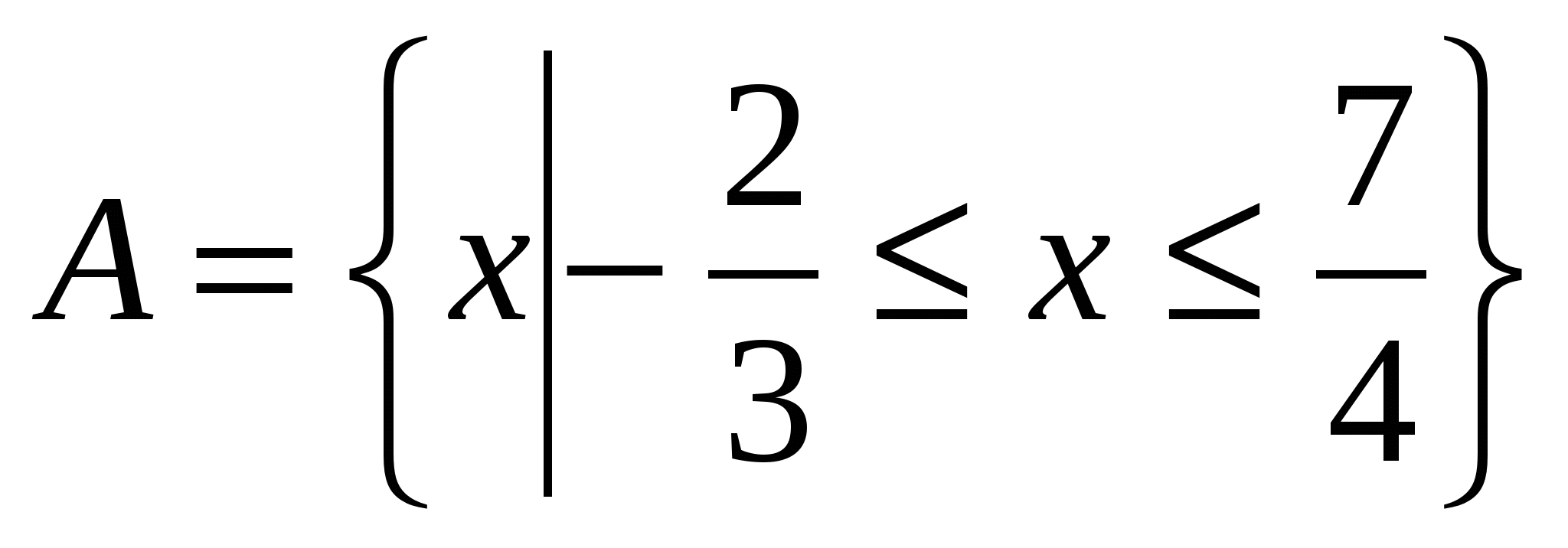 и и 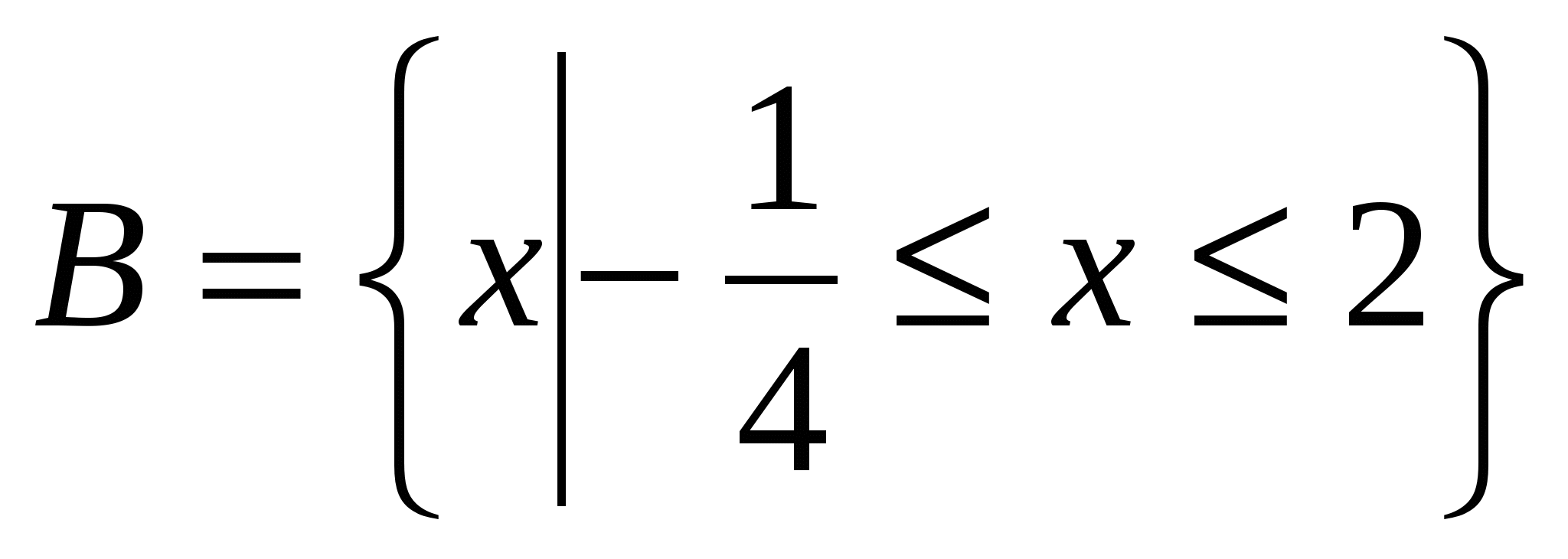 . .
Три множества Р, Н, М изображены тремя прямоугольниками (рис. 1). Отметьте штриховкой области, изображающие множество Х: а) М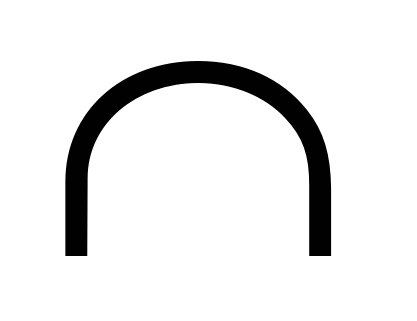 Н; б) Р Н; б) Р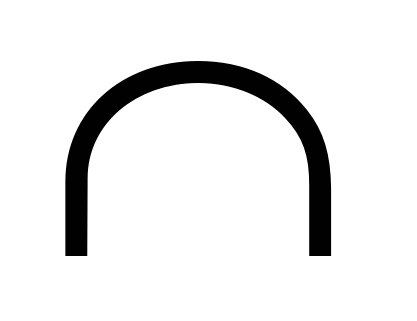 Н; в) (Р Н; в) (Р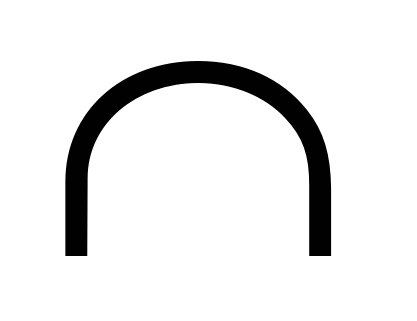 Н) Н)   (Н (Н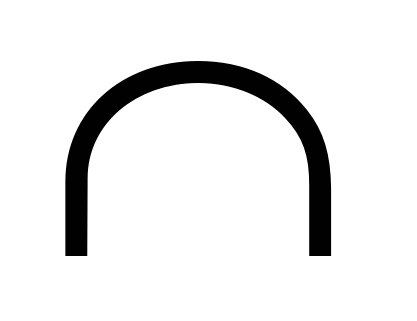 М). М).
Рис. 1.
В – множество правильных многоугольников, Т – множество прямоугольников. Из каких фигур состоит объединение и пересечение множеств В и Т. Нарисуйте по две фигуры из каждого множества.
Даны множества: А ={а, b, с, d, е}, В ={с, d, f, k}, С = {b, с, d, f, m}. Перечислите элементы множеств К=(АВ)С и Р =А В С. Содержится ли элемент m в множестве К, а элемент f в множестве Р?
А – множество чисел, кратных 2, В – множество чисел, кратных 3, С – множество чисел, кратных 5. Укажите характеристическое свойство элементов множества (А В) В)  С и (А С и (А В) В)  С. С.
Найдите объединение и пересечение множеств и дайте графическую иллюстрацию при помощи диаграмм Эйлера - Венна, если:
а) А = {5, 6, 7, 8, 9, 10}, В = {8, 9, 10, 11};
б) А= {х х = 5п, п N}, В= {х ÷ х = 2п, п ÎN};
г) А={х ÷ х = 2п, п ÎN}, В= {х ÷ х = 2п, п ÎN}.
Изобразите на числовой прямой и запишите при помощи неравенства объединение и пересечение множеств Р и Q:
а) Р = 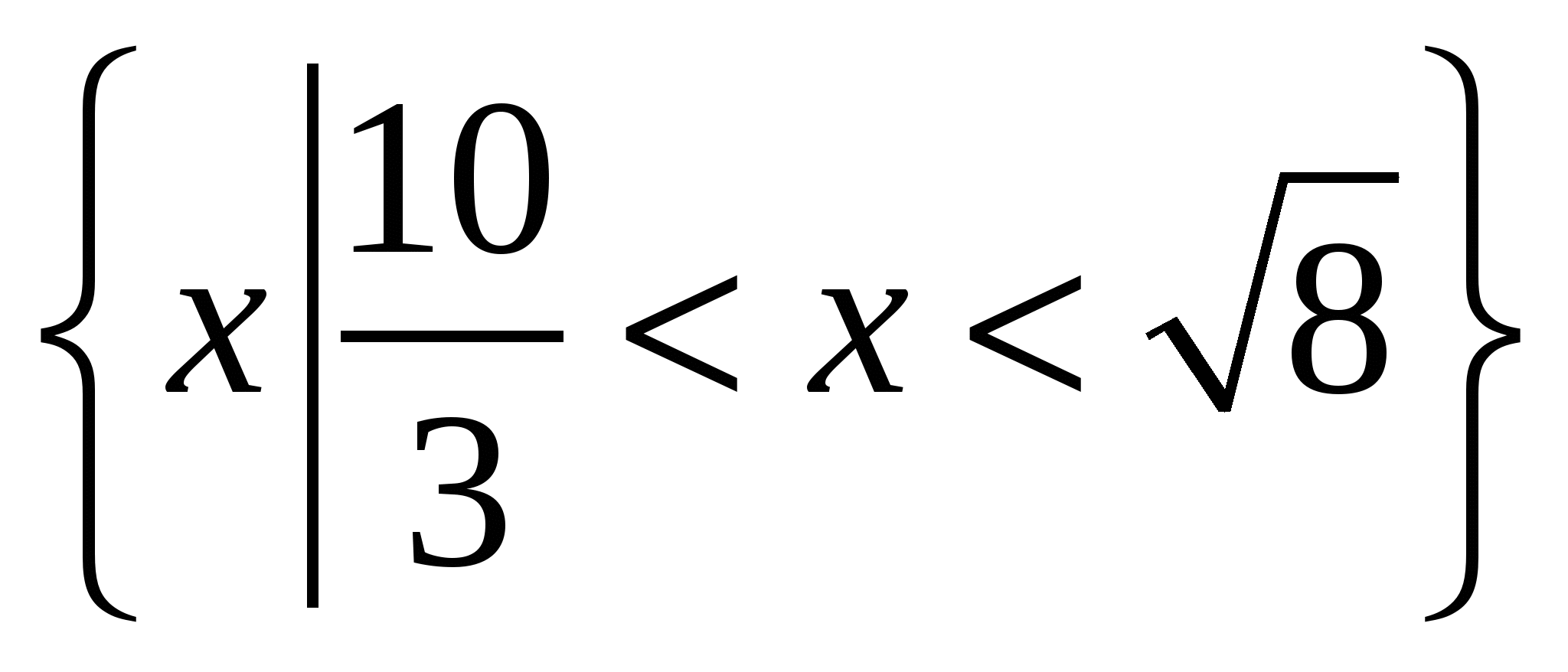 , Q= , Q= ; ;
б) Р =  , Q = , Q = 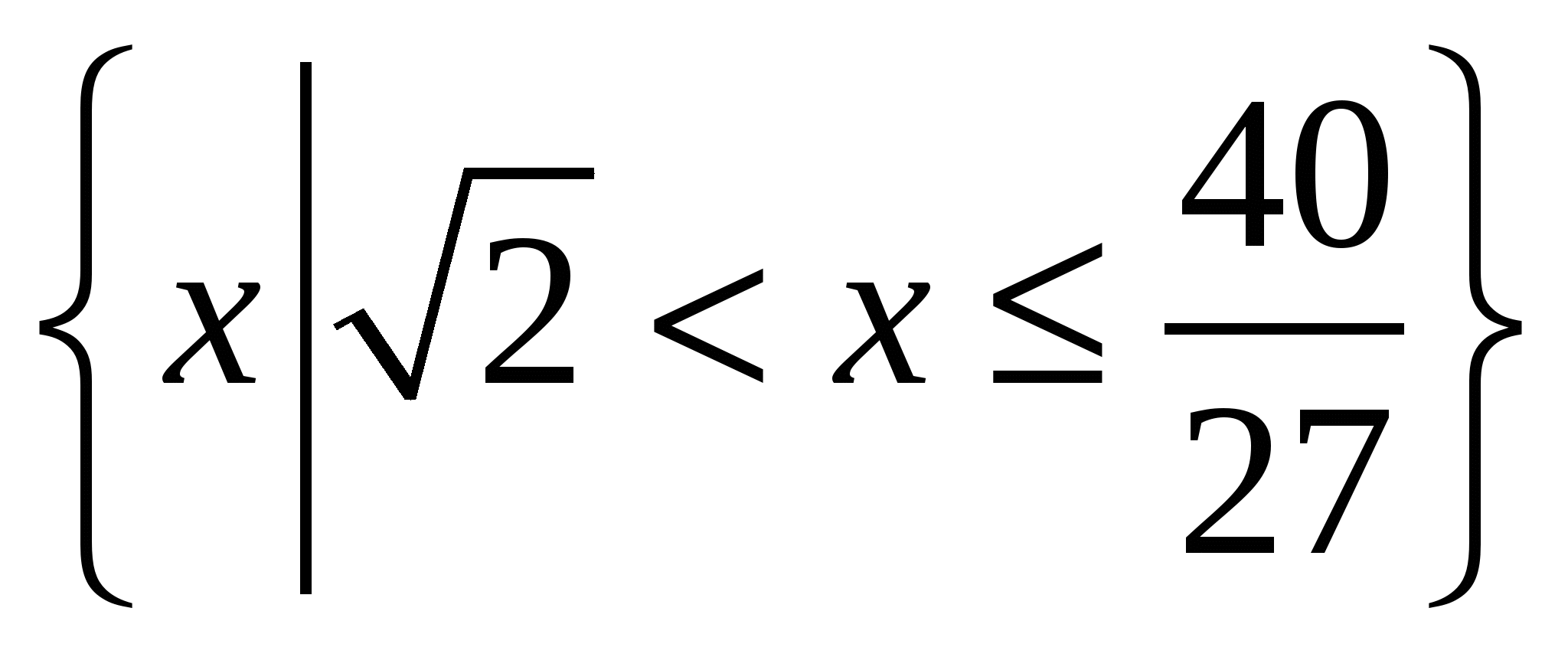 ; ;
в) Р = , Q = , Q = 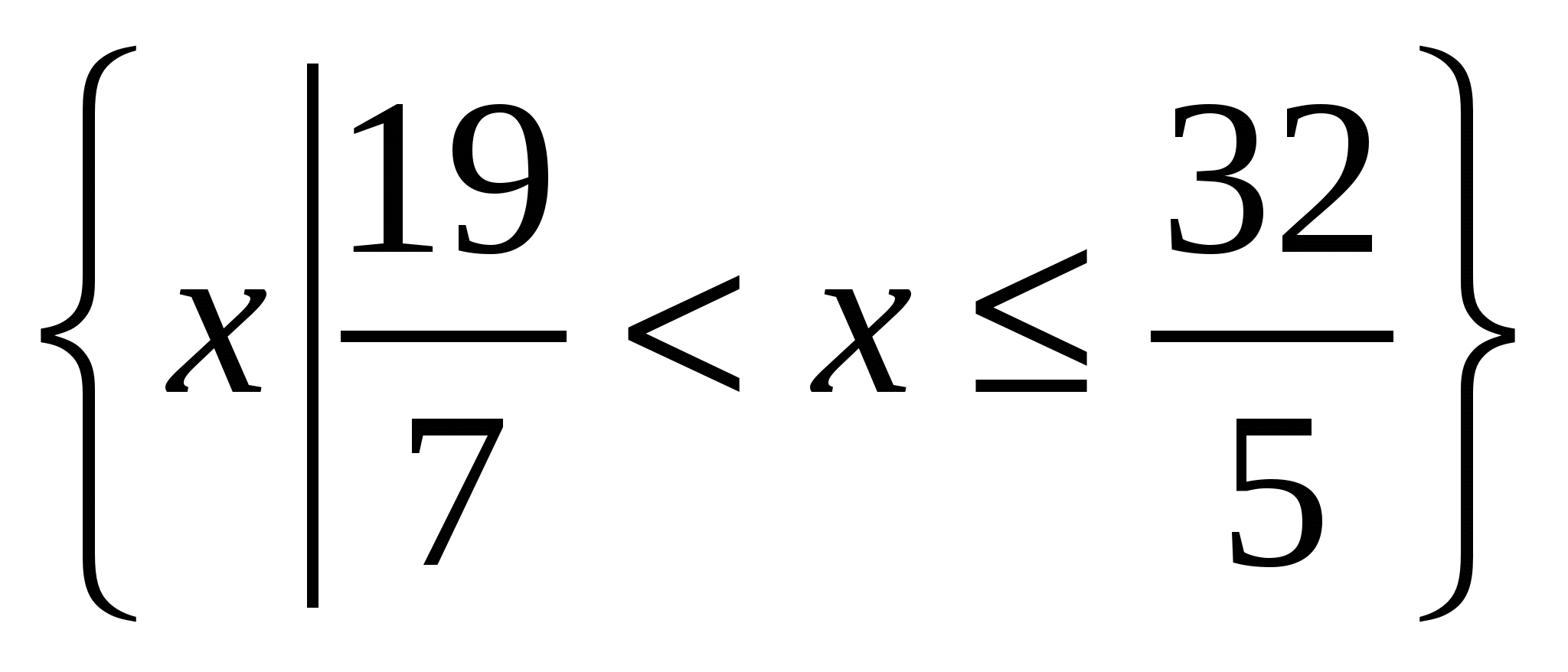
Множество А состоит из натуральных чисел от 2 до 10, множество В – из натуральных чисел от 5 до20. Перечислите элементы множеств А \ В и В \ А.
Р – множество двузначных чисел, М – множество четных натуральных чисел. изобразите данные множества при помощи кругов Эйлера, отметьте штриховкой разность множеств Р и М и укажите характеристическое свойство элементов, принадлежащей этой разности. Верно ли, что Р \ М содержит числа 21; 17?
Дано множество 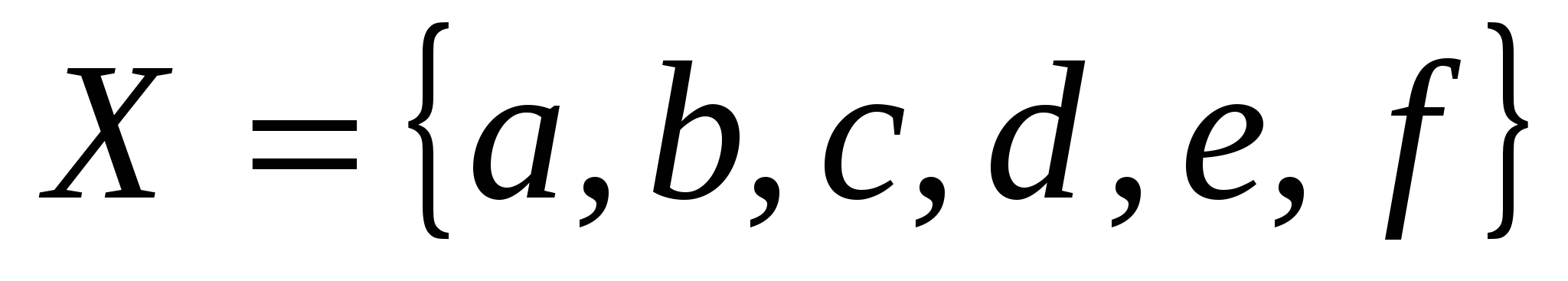 . Запишите два подмножества множества Х и дополнение этих подмножеств до множества Х. . Запишите два подмножества множества Х и дополнение этих подмножеств до множества Х.
Сформулируйте характеристическое свойство элементов дополнения множества Р до множества треугольников, если: а) Р – множество остроугольных треугольников; б) Р – множество равносторонних треугольников.
Найдите дополнение множества У до множества Х, если:
Х – множество точек прямой АВ;
множество точек отрезка АВ;
Х – множество точек квадрата, У – множество точек круга, вписанного в этот квадрат.
Найдите дополнение:
множества четных натуральных чисел до множества N;
множества отрицательных чисел до множества Z;
множества целых чисел до множества Q.
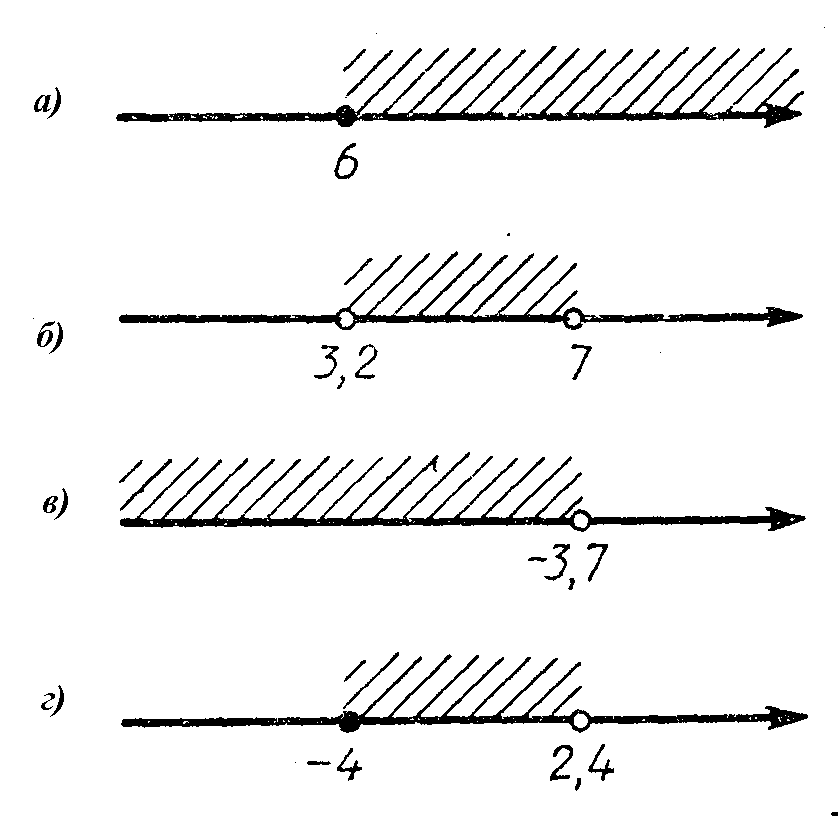
Отметьте на координатной прямой множество А и укажите характеристическое свойство элементов его дополнения до множества R, если: а)  ; б) ; б)  ; в) ; в)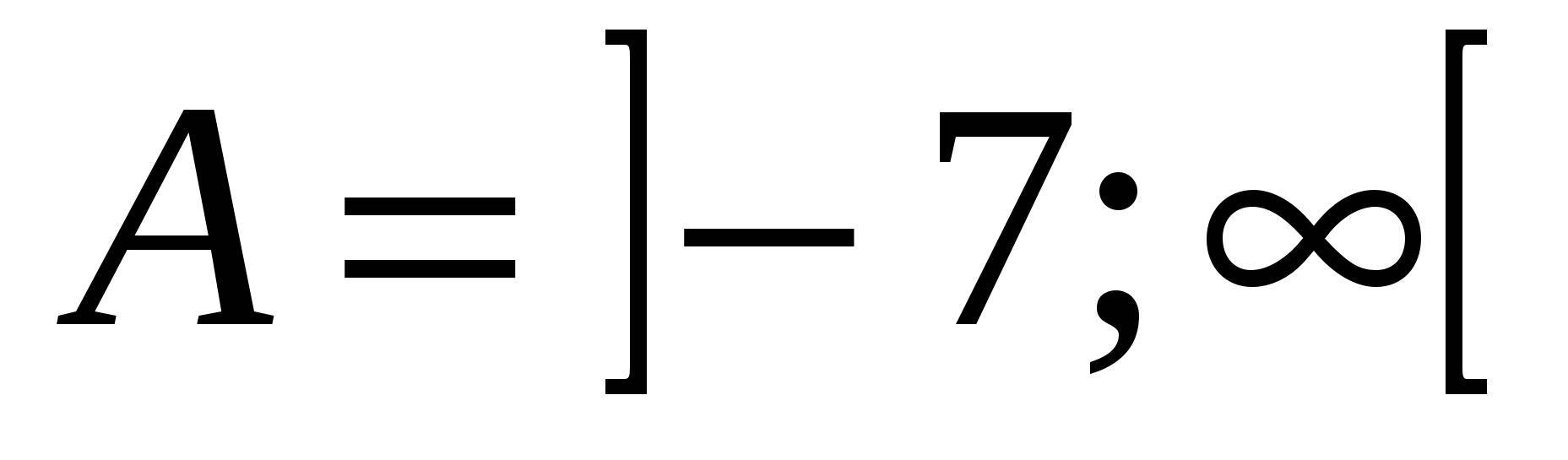 . .
Множества А, В и С таковы, что 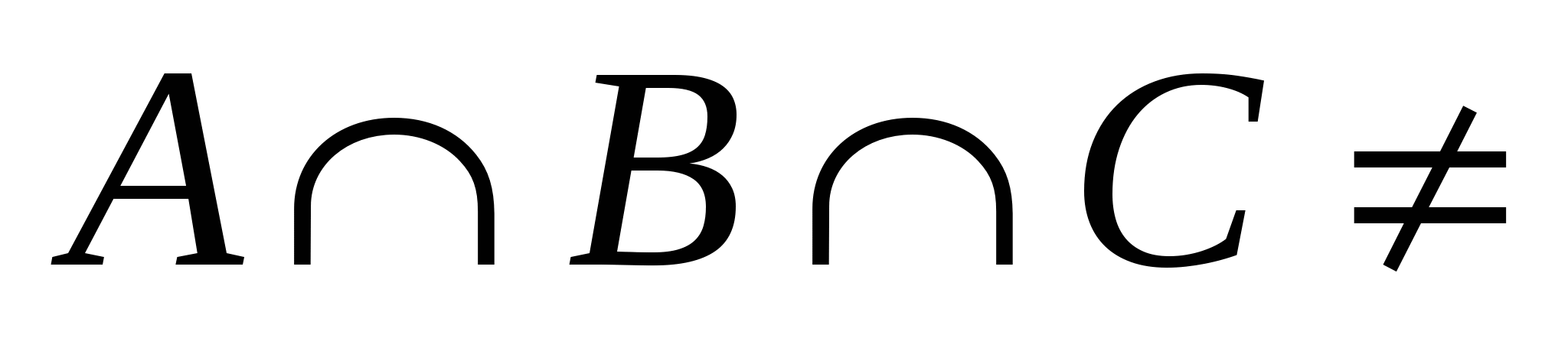 Ø. Изобразите их при помощи кругов Эйлера и отметьте штриховкой области, представляющие множества (А \ В) Ø. Изобразите их при помощи кругов Эйлера и отметьте штриховкой области, представляющие множества (А \ В) 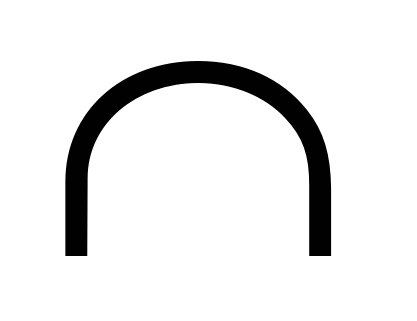 С, А \ В С, А \ В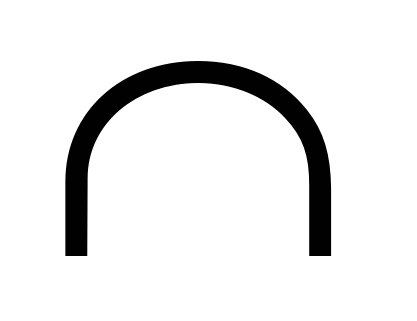 С, А С, А (В \ С), А (В \ С), А В \ С. Для каждого случая сделайте отдельный чертеж. В \ С. Для каждого случая сделайте отдельный чертеж.
А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. постройте круги Эйлера для данных множеств и отметьте штриховкой области, изображающие множества: а) А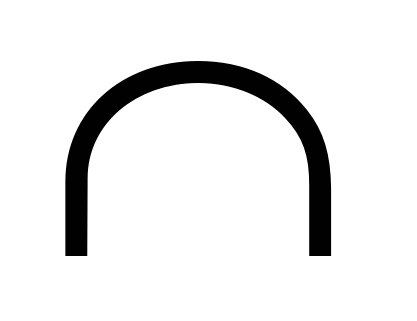 В В С; б) С; б)  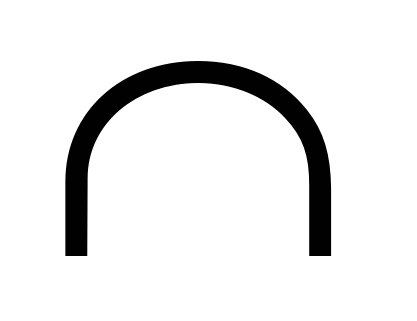 В В С; в) (А С; в) (А В)' В)' С. С.
Постройте три круга, изображающие три попарно пересекающихся множества А, В и С, и выделите штриховкой области, представляющие множества:
а) АВ\С, б) А\СВ\С; в) А\(ВС).
Практическое занятие 1.3. Разбиение множества на классы. Декартово произведение множеств.
Вопросы и задания для подготовки к занятию:
Дайте определение понятиям «разбиение множества на классы»; «декартово произведение множеств».
Какими свойствами обладает и не обладает операция «декартово произведения множеств»?
Найдите В С и С В если
В = {1, 2, 3} C = {10, 20, 30};
В = {а, о, и} C = {м, т, к};
В = {красивая, добрая, вежливая} C = {Маша, Наташа};
В = {0, 00, 000} C = {1, 11, 111};
Для каждого из множеств, приведенных в предыдущем задании, составьте таблицу, в ячейках которой будут расположены элементы соответствующего декартова произведения.
Элементы какого декартова произведения множеств задания 3 могут быть отмечены в декартовой системе координат? Выполните соответствующие построения.
Из множества Р = {1, 2, 3, 4, 5, 6, 7, 8, 9} выделили подмножества А, В и С. В каком случае произошло разбиение множества Р на классы:
А ={1, 3, 5}, В = {2, 4, 6, 8}, С = {7, 9};
А = {5}, В = {3, 4, 8, 9}, С = {1, 6};
А = {1, 3, 5}, В = {2, 4, 6, 8}, С = {5, 7, 9};
А = {1, 3}, В = {4, 6, 8}, С = {5, 6, 9}.
Запишите все двузначные числа, цифры десятков которых принадлежат множеству А ={4, 5, 6}, а цифры единиц – множеству В={3, 7}.
Задания для самостоятельной работы
Множество А состоит из 3, 4, 5, 6, 7, 8, 9; множество В – его подмножество, состоящее из чисел, которые делятся на 3; множество С – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 1; множество Е – подмножество. Состоящее из чисел, которые при делении на 3 дают в остатке 2. Можно ли утверждать, что множество А разбивается в этом случае на попарно непересекающиеся подмножества В, С и Е?
Проверьте, выполняются ли условия классификации, если: а) множество углов разбили на острые, тупые и прямые; б) множество звуков русского языка – на гласные и согласные.
Из множества Т треугольников выделили два подмножества: Х - подмножество прямоугольных треугольников и У – подмножество равнобедренных треугольников. Постройте для данных множеств круги Эйлера; установите, на сколько непересекающихся областей разбился круг, изображающий множество Т, и все множества, изображенные этими областями, задайте описанием характеристического свойства. При помощи скольких свойств произведено разбиение множества треугольников на классы?
Изобразите при помощи кругов Эйлера множество натуральных чисел и его подмножества: четных чисел и чисел, кратных 7. Можно ли утверждать, что множество N разбито:
на два класса: четных чисел и чисел, кратных 7;
на 4 класса: четных чисел, кратных 7; нечетных чисел, некратных 7; четных чисел, некратных 7; нечетных чисел, кратных 7?
Изобразите на координатной плоскости элементы декартова произведения множеств Х и У, если:
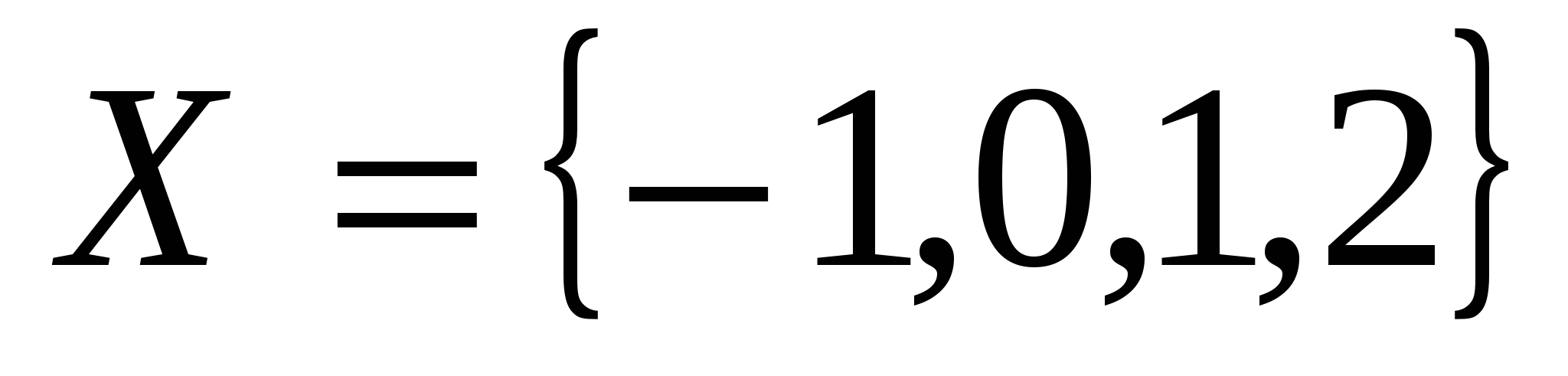 и и 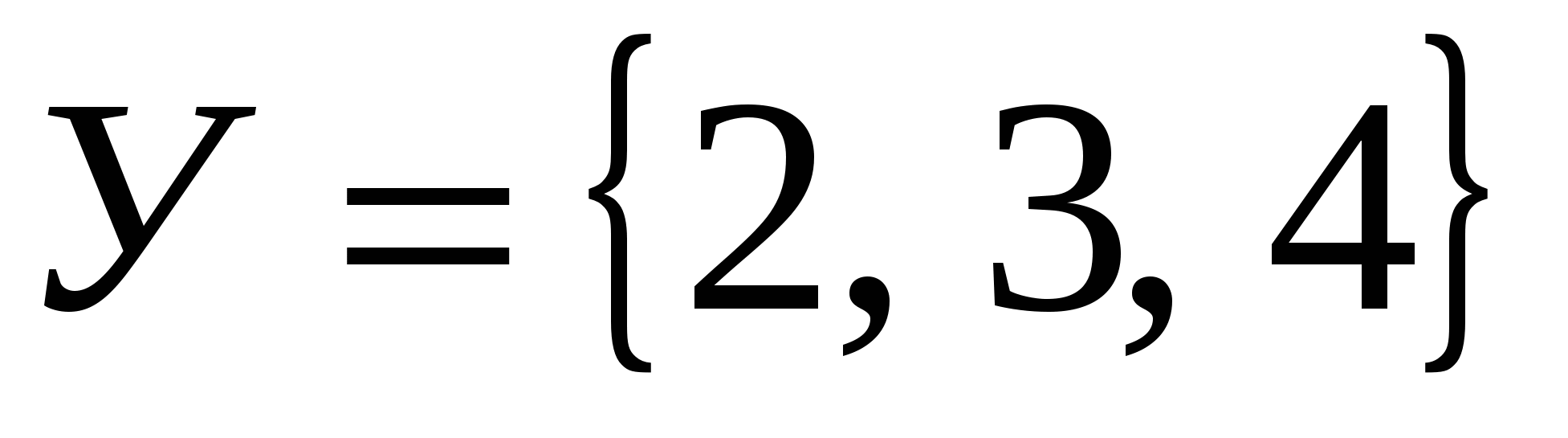 ; ;
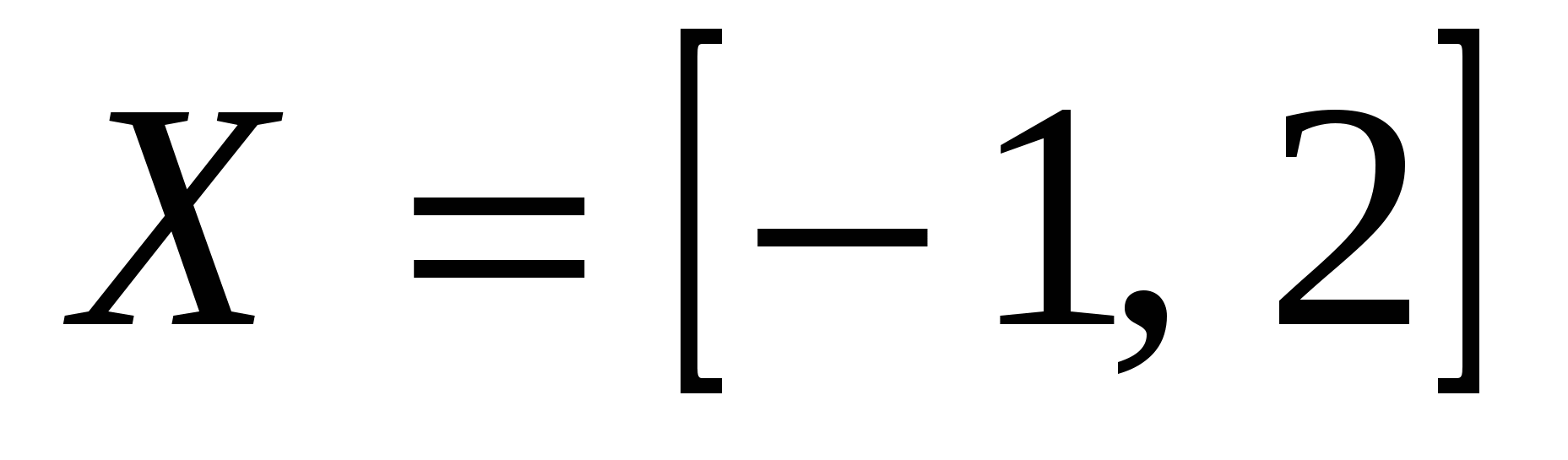 и и 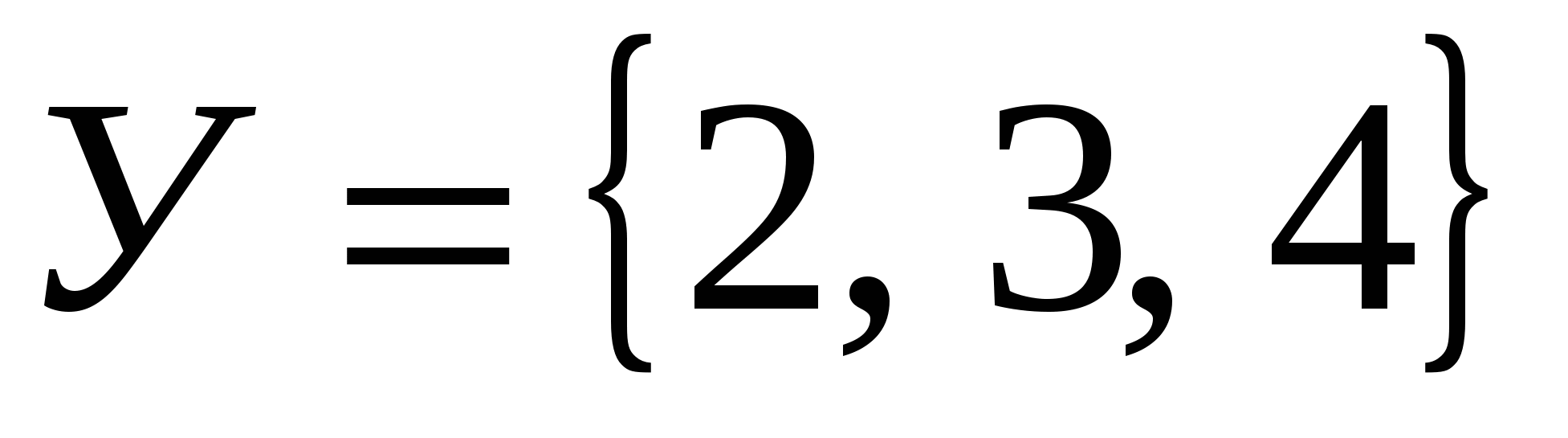 ; ;
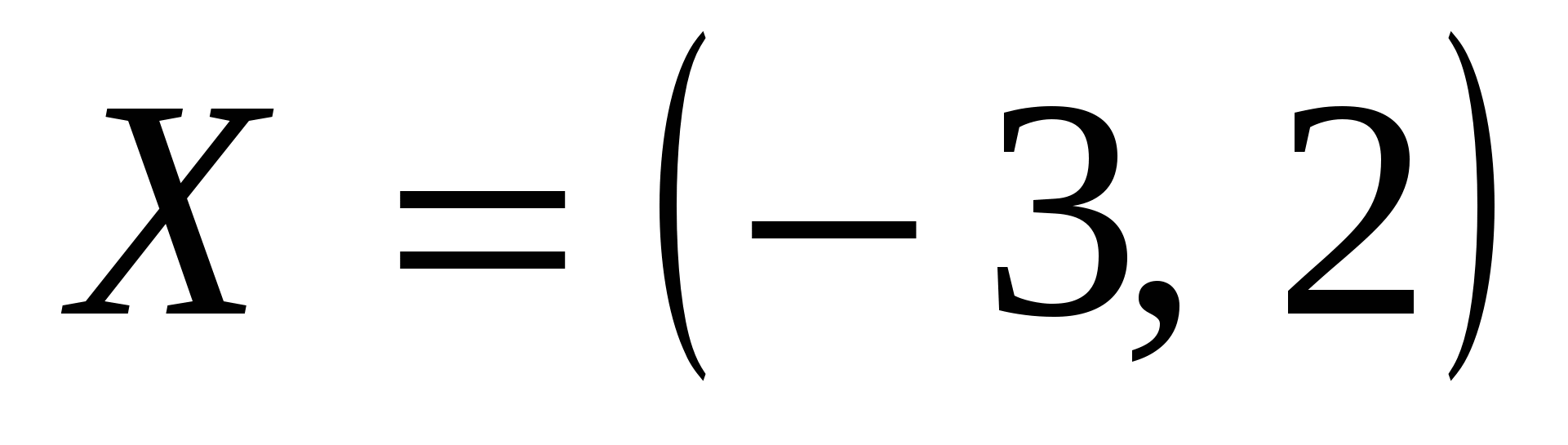 и У=R; и У=R;
Х=R и 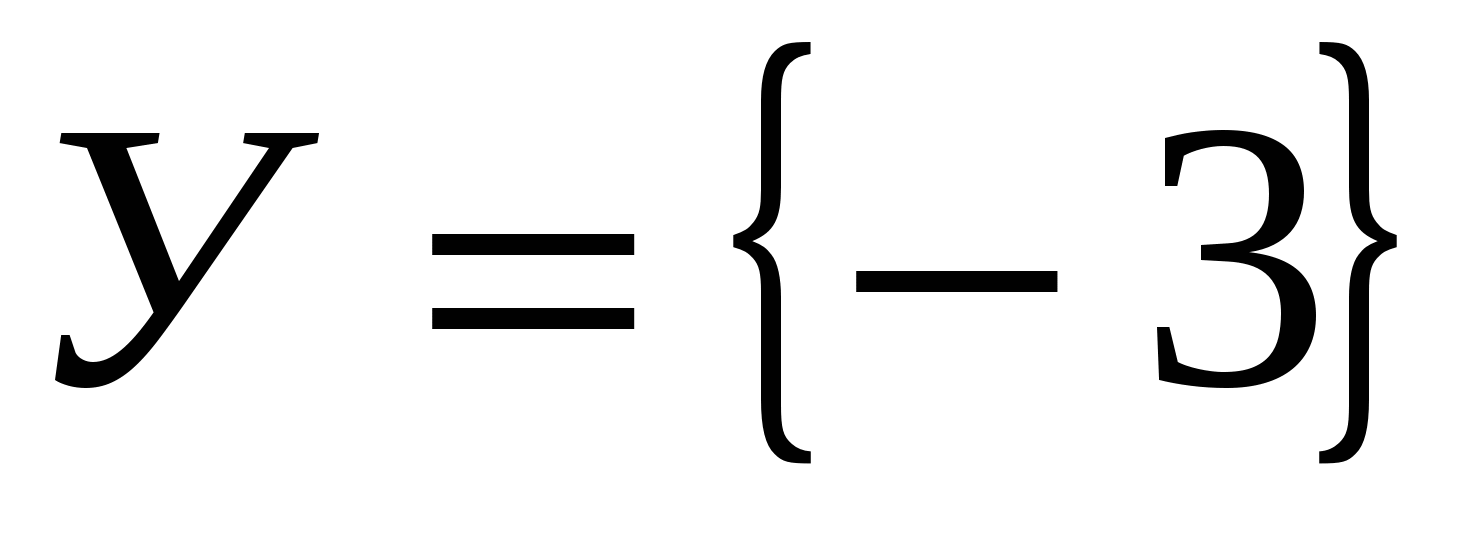 . .
Фигуры, приведенные на рисунке, являются результатом изображения накоординатной плоскости декартова произведения множеств Х и У. Укажите для каждой фигуры эти множества.
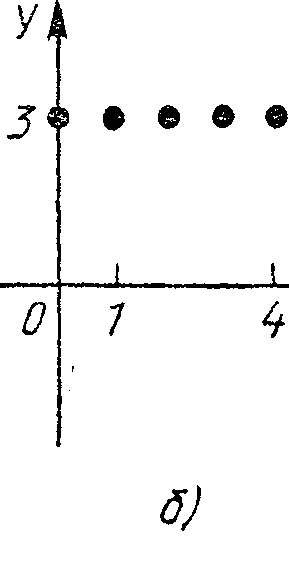 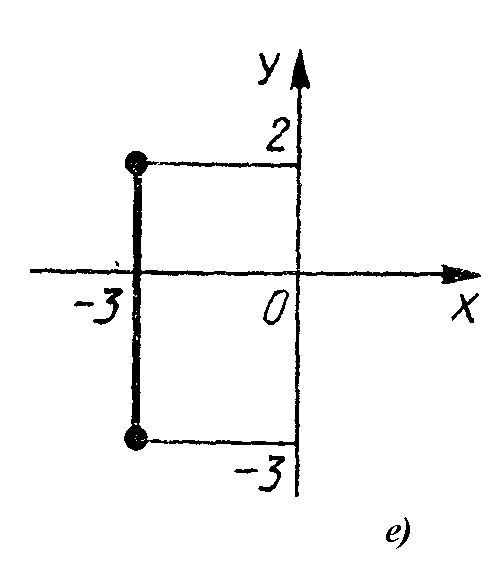 
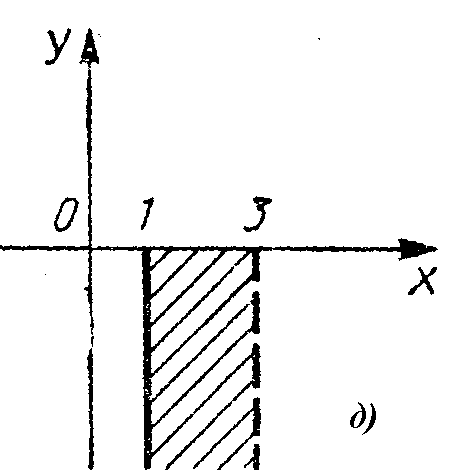
На координатной плоскости постройте прямую, проходящую через точку Р (-2, 3) и параллельную оси ОХ. Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой.
Найдите декартовы произведения множеств и изобразите их элементы на координатной плоскости:
А = {х÷ хÎ R, х > 0}; В = {у÷ у Î R, у < 0}
А = {х÷ хÎ R, х = 2}; В={у÷ у Î R , у > 0}
А = {х÷ хÎ R, -1 < х < 1}; В={у÷ у Î R, 0 < у < 1}.
Практическое занятие 1.4. Число элементов в объединении, пересечении, разности и декартовом произведении множеств.
Вопросы и задания для подготовки к занятию:
Закончите равенства
п(АВ) = , если АВ = ;
п(АВ) = , если АВ ;
п(АВ)=, если АВ = ;
п(АВ)= , если АВ ;
п(АВ)=
Условия задач даны на схемах. Найдите численности множеств, которые отмечены знаком «?»
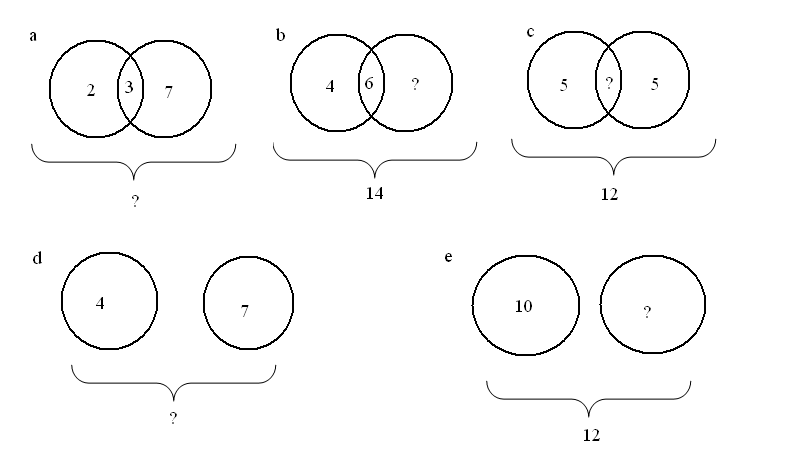
В группе туристов, состоящей из 100 человек, 10 не знали ни немецкий, ни французский языки, 75 знали немецкий, 83 знали французский. Сколько туристов знали два языка?
Из 32 школьников 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 человек занимаются и в той, и в другой секции. Сколько человек не занимаются ни в волейбольной, ни в баскетбольной секции.
Множество А содержит 7 элементов. Сколько элементов в множестве В, если декартово произведение А×В состоит из:
42 элементов;
7 элементов;
А×В=Ø.
Задания для самостоятельной работы
Даны 40 чисел, из них 10 чисел кратны 3; 15 чисел кратны 2; 20 чисел не кратны ни 2, ни 3. Сколько среди данных 40 чисел, кратных 6?
На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги А, В, С. Результаты опроса оказались таковы: книгу А читали 25 учащихся, книгу В – 22, книгу С – также 22, Книгу А и В читали 33 ученика, А или С – 32, В или С -31; все три книги прочли 10 учащихся. Сколько учеников прочли только по одной книге? Сколько учащихся не читали ни одной из этих трех книг?
Решите нижеприведенные задачи методом перебора всех возможных вариантов, а затем покажите, что решение этих задач связано с определением числа элементов декартова произведения множеств:
В костюмерной танцевального кружка имеются белые и розовые кофты, а также синие, черные и коричневые юбки. Сколько можно из них составить различных костюмов?
Сколько трехзначных чисел можно составить, используя цифры 4 и 7?
На вершину горы ведут две дороги. Сколькими способами можно подняться и спуститься с вершины?
Сколько разных наборов можно составить из книги и блокнота, если имеются 20 видов различных книг и 15 видов различных блокнотов?
Практическое занятие 1.5. Понятия.
Вопросы и задания для подготовки к занятию:
Ответьте на следующие вопросы:
Какое свойство называется существенным?
Что такое понятие?
Что называется содержанием понятия? Объемом понятия?
Что называется определением понятия?
Какие способы определения понятия вы знаете? Охарактеризуйте каждый из них. Приведите примеры.
Сформулируйте требования к определению понятий. Раскройте их.
Можно ли при помощи свойства «иметь прямой угол» выделить подмножество квадратов из множества:
ромбов,
параллелограммов;
четырехугольников?
Если нет, то укажите свойство при помощи которого это можно сделать.
В следующих определениях выделите определяемое и определяющее понятие, родовое понятие (по отношение к определяемому) и видовое отличие:
Параллелограммом называется четырехугольник, у которого противоположные стороны равны и параллельны;
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
Задания для самостоятельной работы
Проанализируйте следующие определения, определите их структуру и назовите способ определения:
Равнобедренный треугольник - это треугольник, у которого две стороны равны между собой.
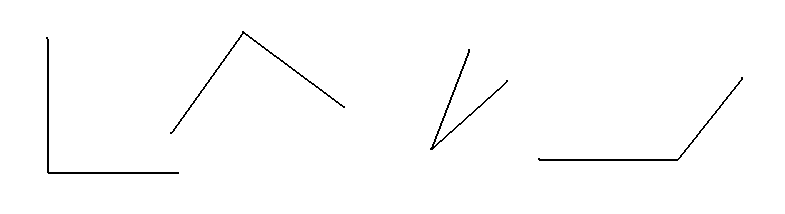
это прямые углы это непрямые углы
(учебник М.И. Моро, 2 кл., 1987. С.47)
Рассмотри рисунок:
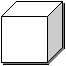 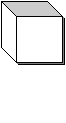
Как ты думаешь, что на нем изображено?
Ты прав: это кубический сантиметр. Наименование этой меры записывается так:
1 куб.см. или 1 см3. (И.И. Аргинская, Математика 1 кл., 1997г.).
Квадрант - один из четырех прямых углов на плоскости, образованных двумя перпендикулярными осями координат.
Квадратом называется прямоугольник, у которого стороны конгруэнтны.
Геометрическая прогрессия - числовая последовательность, первый член которой не равен 0, а каждый член, начиная со второго, равен предыдущему члену, умноженному на некоторое постоянное и не равное 0 число q, называемое знаменателем прогрессии.
Установите, каким способом определяются в начальной математике понятия: «математическое выражение», «нечетное число». (по учебнику Моро, Аргинской и Петерсон).
Есть ли ошибки в определениях:
Остроугольным треугольником называется треугольник, у которого есть острый угол;
Прямоугольным называется треугольник, у которого есть прямой угол.
Прямоугольником называется четырехугольник, у которого противоположные стороны равны.
Биссектрисой угла называется прямая, делящая угол пополам;
Сложением называется действие, при котором числа складываются;
Равносторонним называется треугольник, у которого равны все стороны и все углы;
Изобразите с помощью кругов Эйлера отношения между объектами понятий А, В и С, если:
А – «четырехугольник», В – «трапеция», С – «прямоугольник»
А – «натуральное число, кратное 3», В – «натуральное число, кратное 4», С – «натуральное число».
Практическое занятие 1.6. Высказывания и предикаты.
Вопросы и задания для подготовки к занятию:
Найдите значения истинности высказываний:
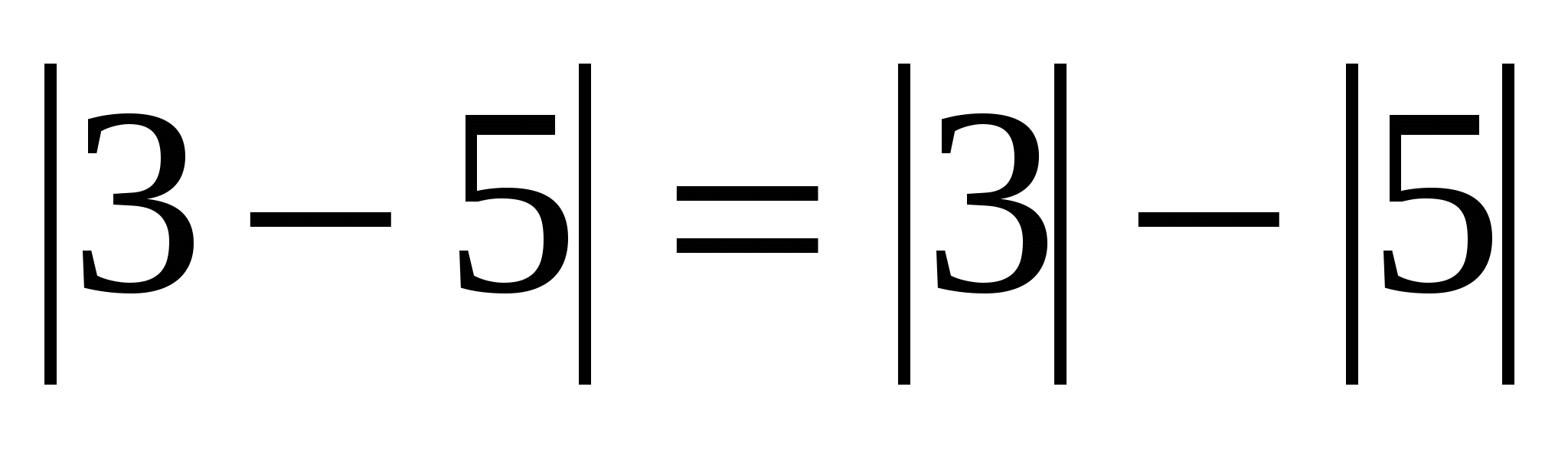
Объединением множеств 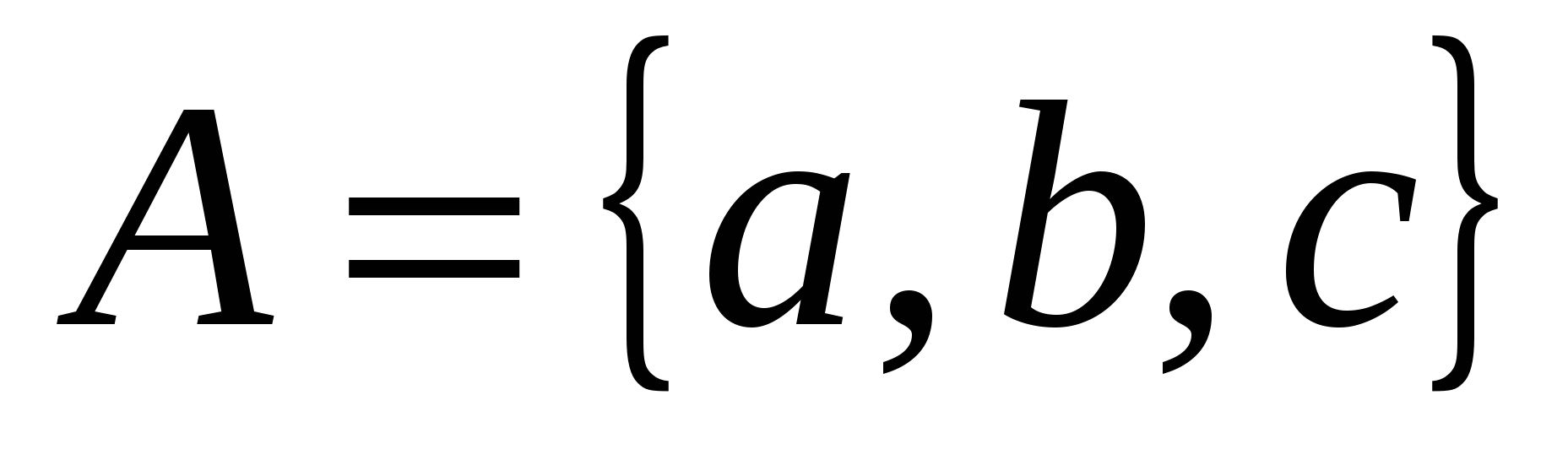 и и  является множество является множество 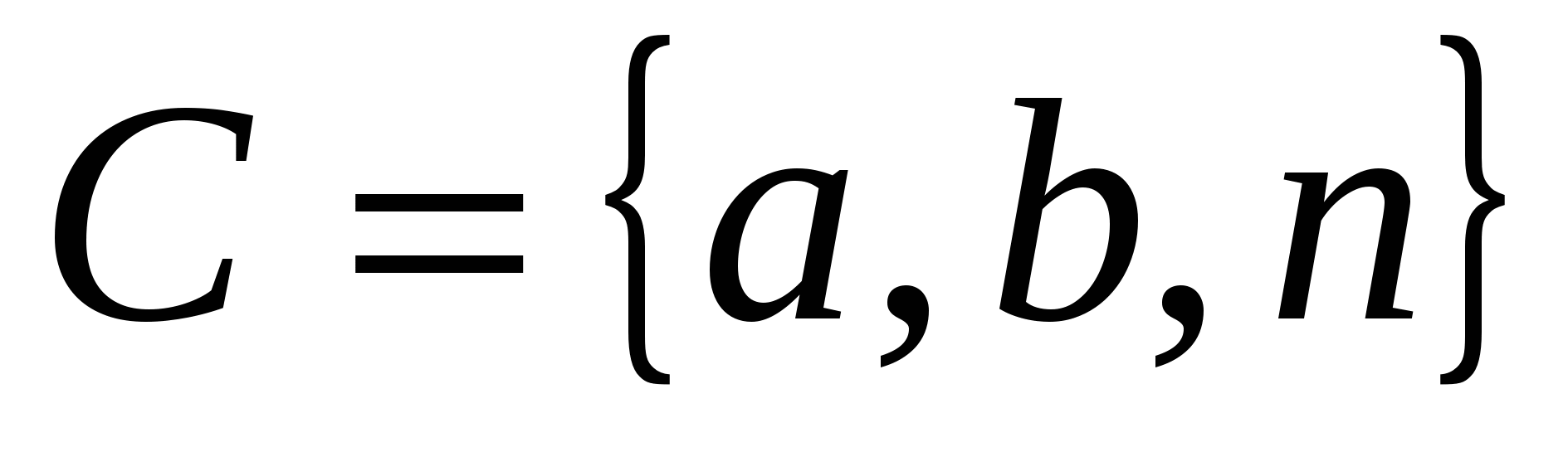 ; ;
23 >32
Среди следующих предложений укажите высказывания и предикаты, поясните свой ответ:
2 – натуральное число;
произведение чисел 2 и 7 равно 15;
х =11 является решением неравенства 2х - 1>5;
разность чисел х и 3 равна 7.
На множестве N задан предикат С(х): «число х – делитель 12». Сформулируйте высказывания С(4), С(8), С(5). Найдите их значения истинности.
Задания для самостоятельной работы
Предикат «х>у» задан на множестве R×R. Назовите две пары чисел, при подстановке которых в предикат получается:
истинное высказывание;
ложное высказывание.
Изменится ли множество истинности предиката А(х): «х2 - 4х – 5 = 0», если в качестве возможных значений переменной х рассмотреть:
множество N;
множество R ?
Найдите множества истинности предикатов:
 ; ;
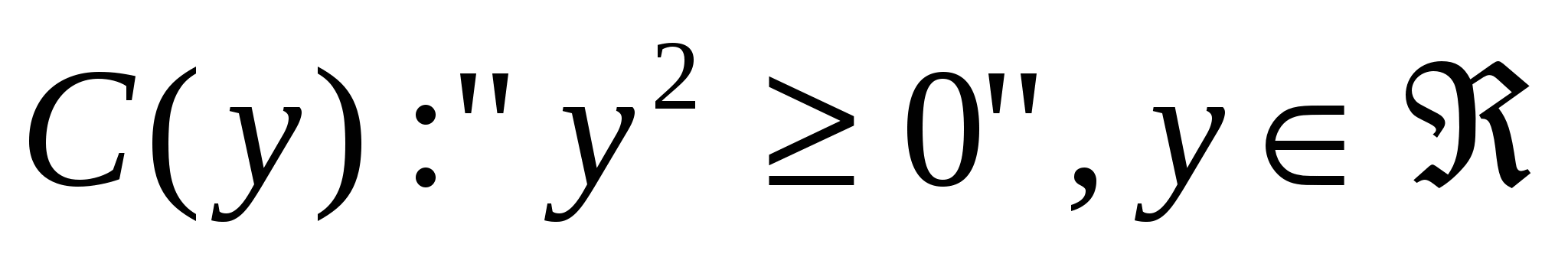 ; ;
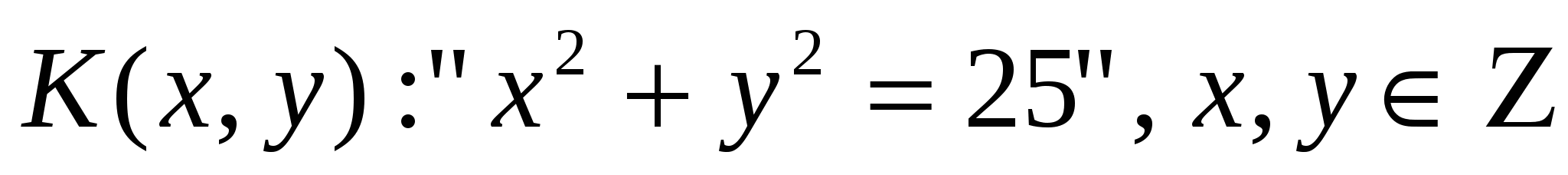 . .
Из предложений «Треугольник АВС равнобедренный» и «Треугольник АВС равносторонний» образуйте составные при помощи слов «или», «если…, то».
Среди следующих предложений укажите составные высказывания, выделите в них элементарные высказывания и логические связки:
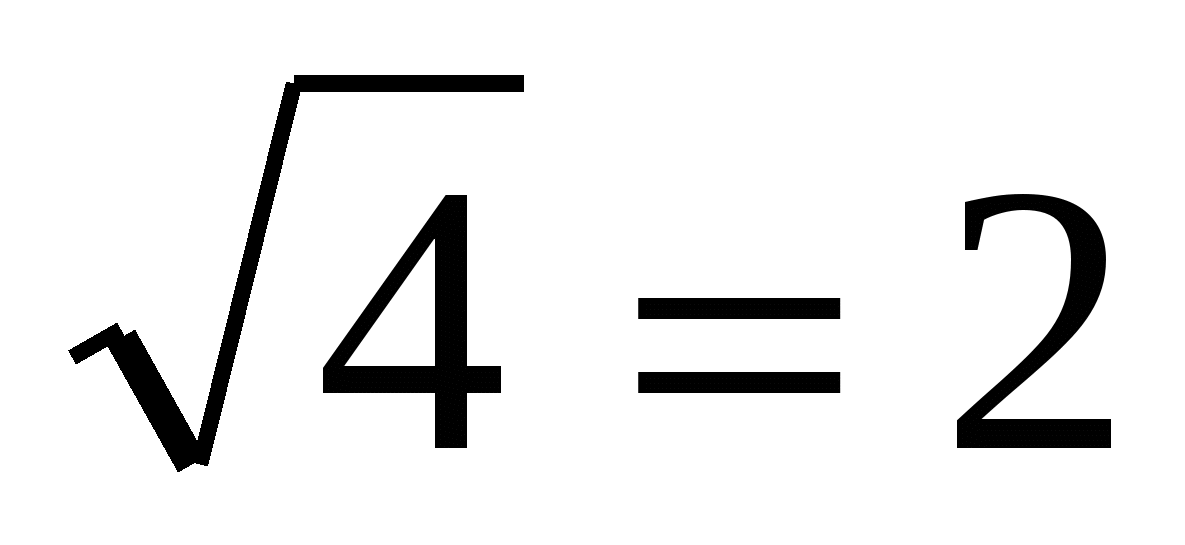 или или 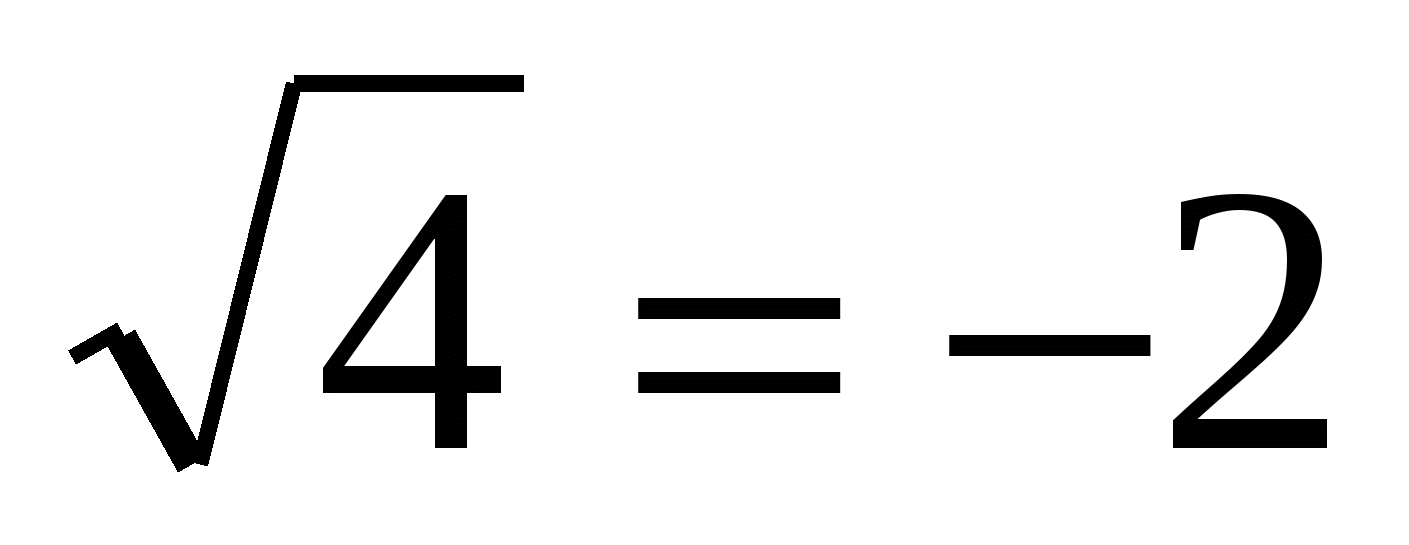 ; ;
Противоположные стороны параллелограмма равны и параллельны;
Число делится на три тогда и только тогда, когда сумма цифр в его десятичной записи делится на 3;
Число 13 простое и не делится на 2;
Если число делится на 6, то оно делится и на 2.
Практическое занятие 1.7. Конъюнкция и дизъюнкция высказываний и высказывательных форм. Отрицание высказываний.
Вопросы и задания для подготовки к занятию:
Дайте определение следующим понятиям:
Конъюнкция высказываний.
Дизъюнкция высказываний.
Конъюнкция высказывательных форм.
Дизъюнкция высказывательных форм.
Выясните в каких случаях можно найти значения истинности высказываний А В и А В и А В: а) А – «истинно»; б) А – «ложно». В: а) А – «истинно»; б) А – «ложно».
Обозначьте элементарные высказывания буквами и запишите следующие высказывания с помощью символов логики высказываний:
В параллелограмме АВСД угол А прямой, а диагонали взаимно перпендикулярны;
Треугольник АВС является прямоугольным или остроугольным.
Задания для самостоятельной работы
Даны высказывания: А – «сегодня температура воздуха ниже 0С», В – «сегодня ясно», С – «я пойду кататься на лыжах», Е – «я пойду кататься на коньках». Сформулируйте высказывания, имеющие структуру:
Пусть предикаты А(х) и В(х) заданы на некотором множестве Х. Сформулируйте условия, при которых: а) 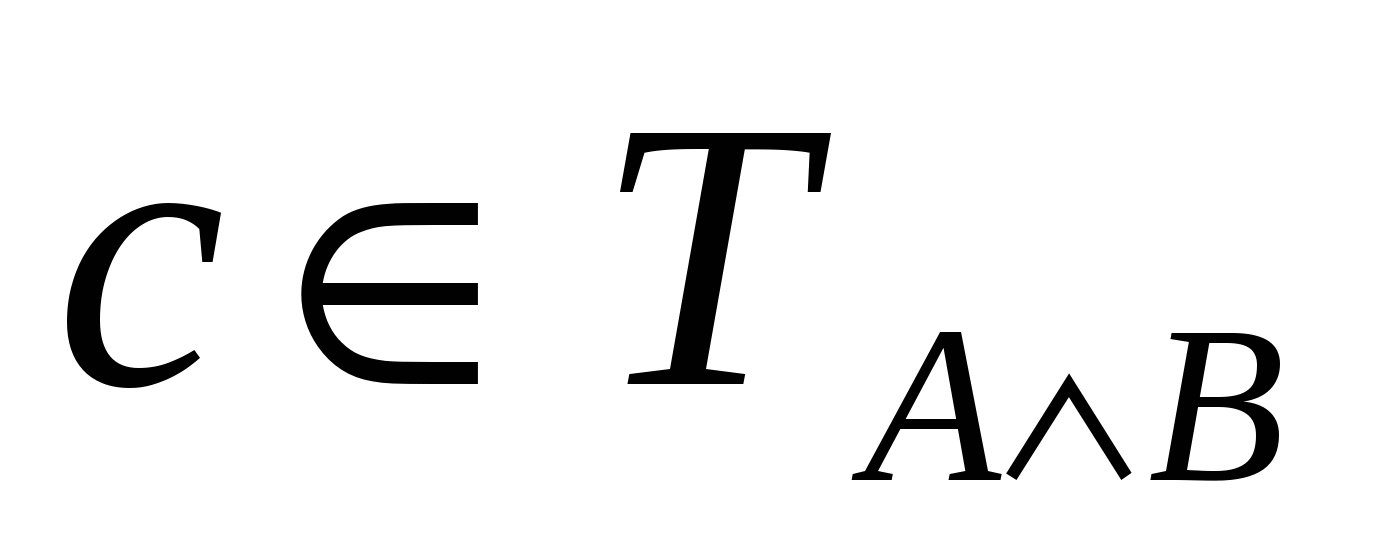 ; б) ; б)  ; в) ; в)  .(с .(с  Х) Х)
На множестве 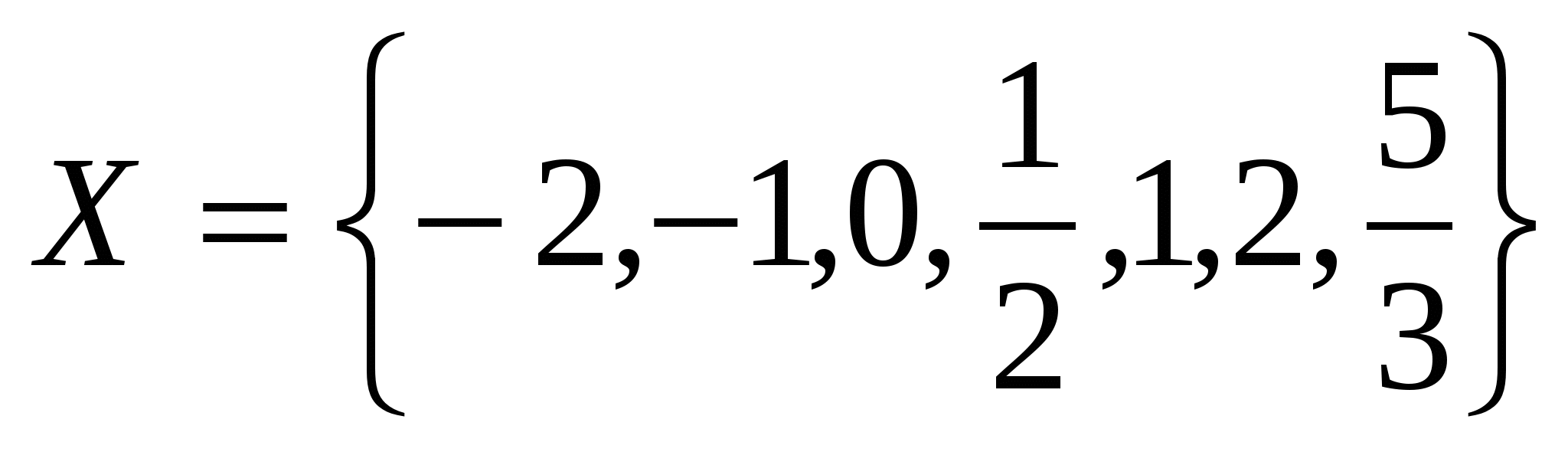 заданы предикаты С(х): «число х натуральное», Н(х): «число х дробное». Сформулируйте высказывания С(1) заданы предикаты С(х): «число х натуральное», Н(х): «число х дробное». Сформулируйте высказывания С(1) Н(1), С(0) Н(1), С(0) Н(0), С(-2) Н(0), С(-2) Н(-2) и найдите их значения истинности. Верно ли, что Н(-2) и найдите их значения истинности. Верно ли, что 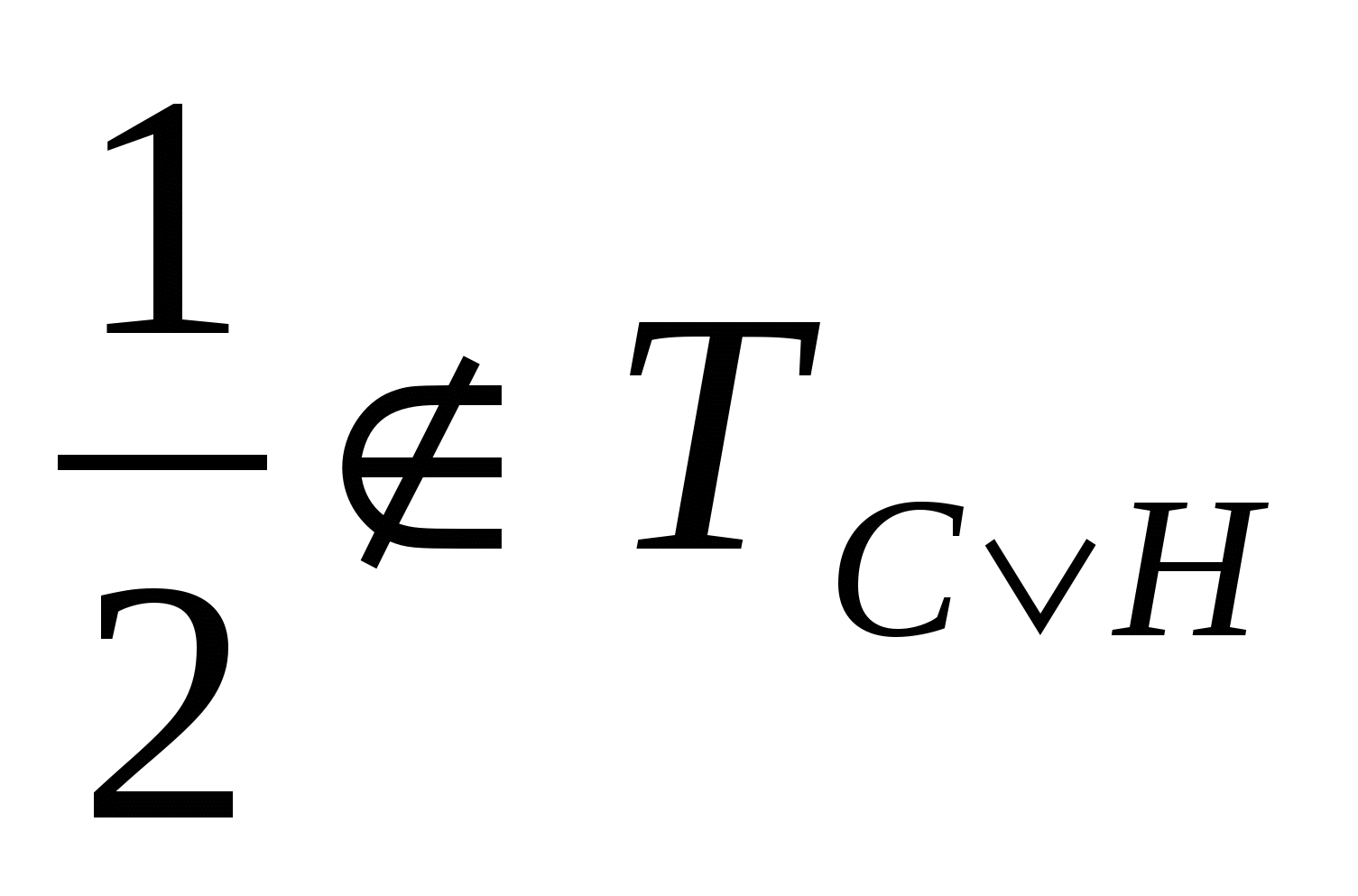 ? ?
Составьте таблицы истинности для следующих высказываний
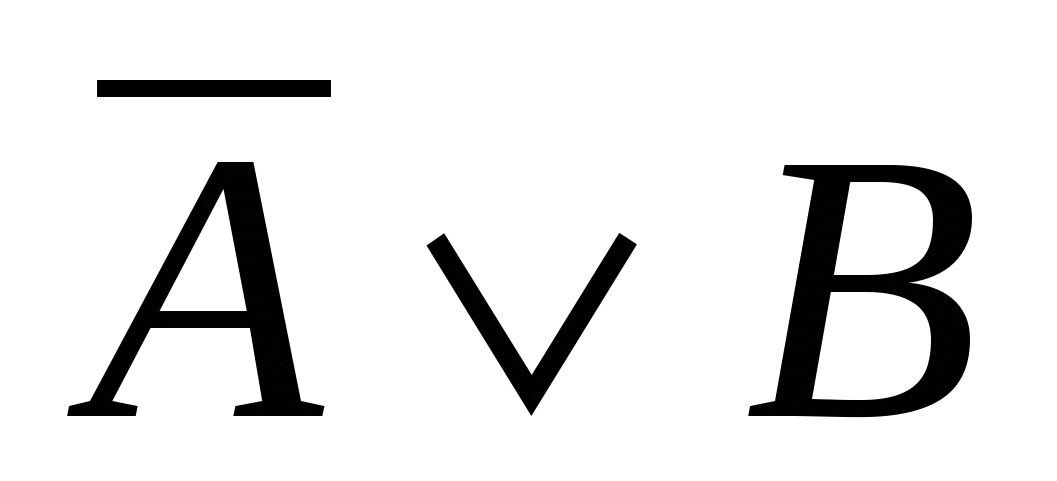 ; ;
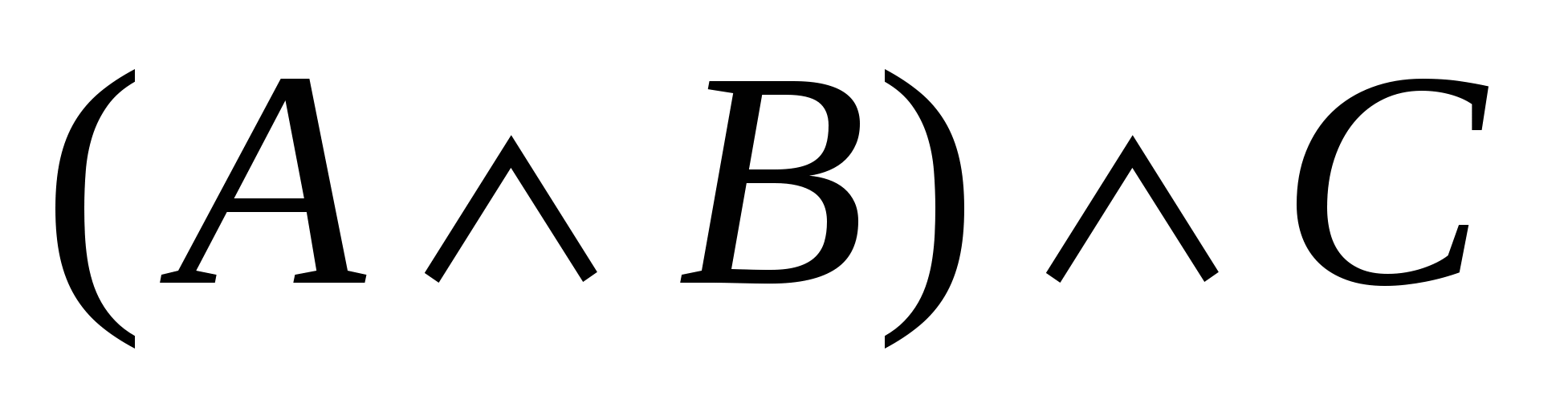 ; ;
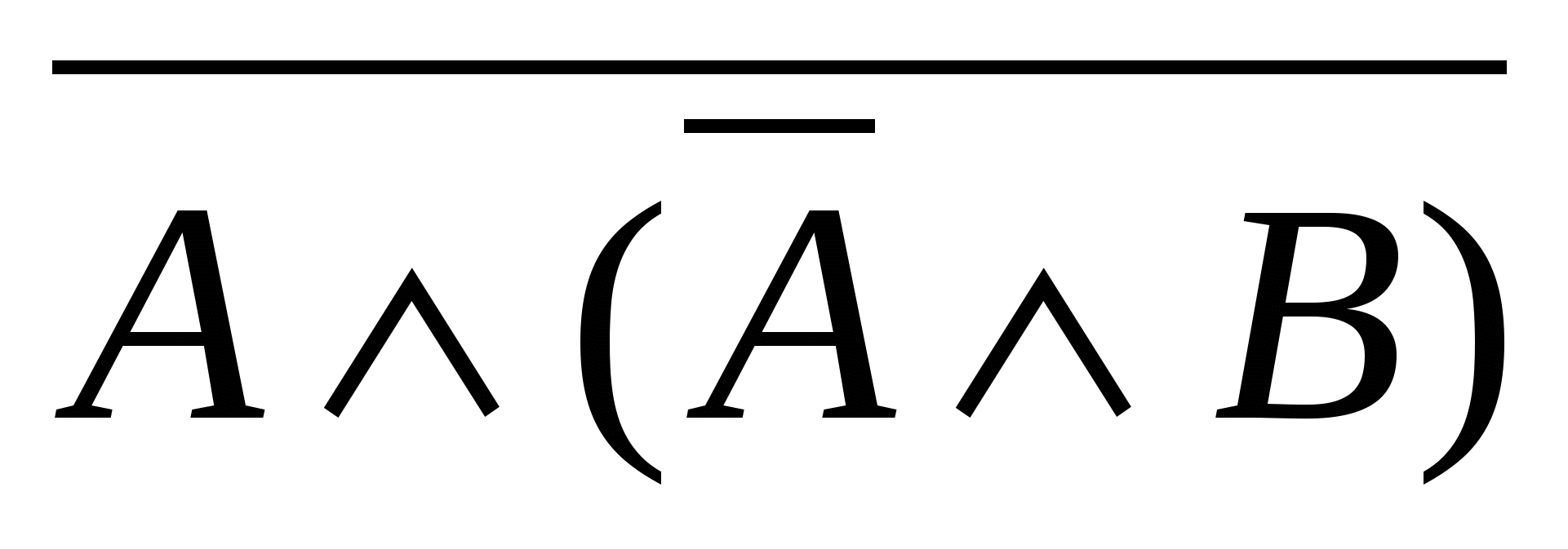 ; ;
Известно, что А «истинно», В – «истинно», Х – «ложно», С – «ложно». Найдите значение высказывания
А или отрицание Х;
отрицание А и В;
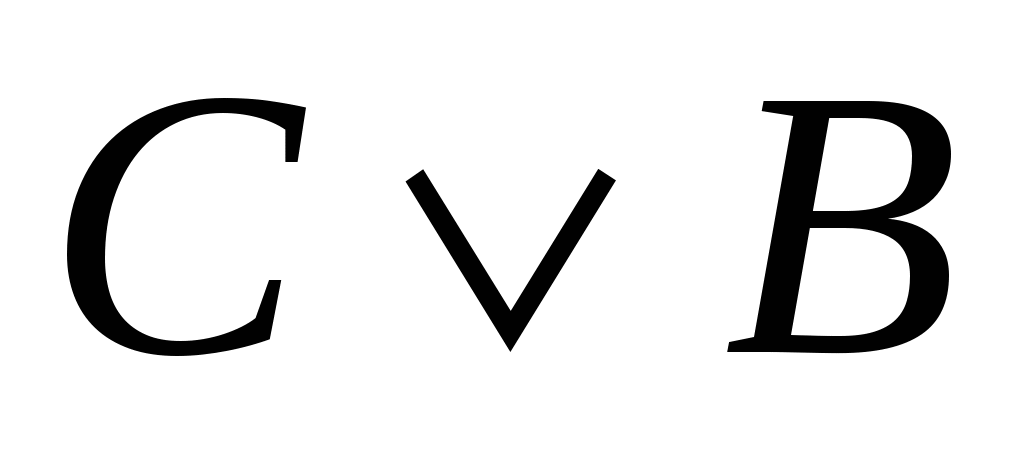 ; ;
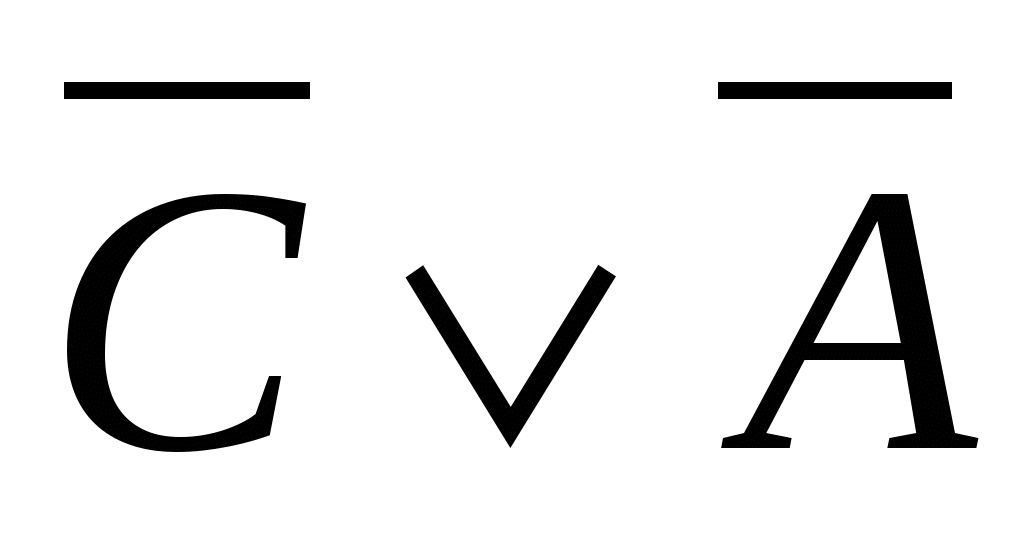 ; ;
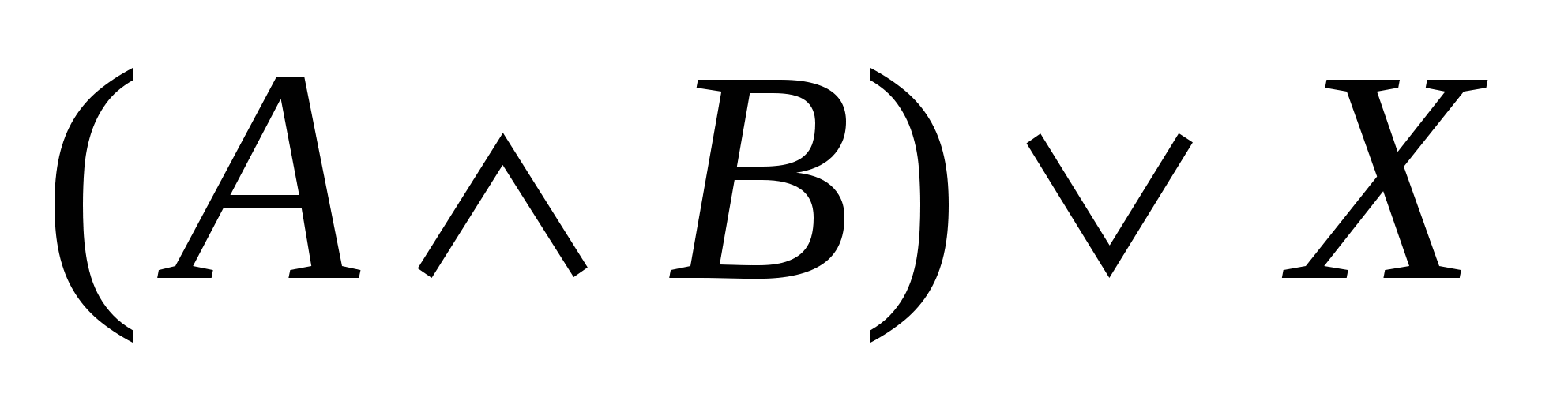 ; ;
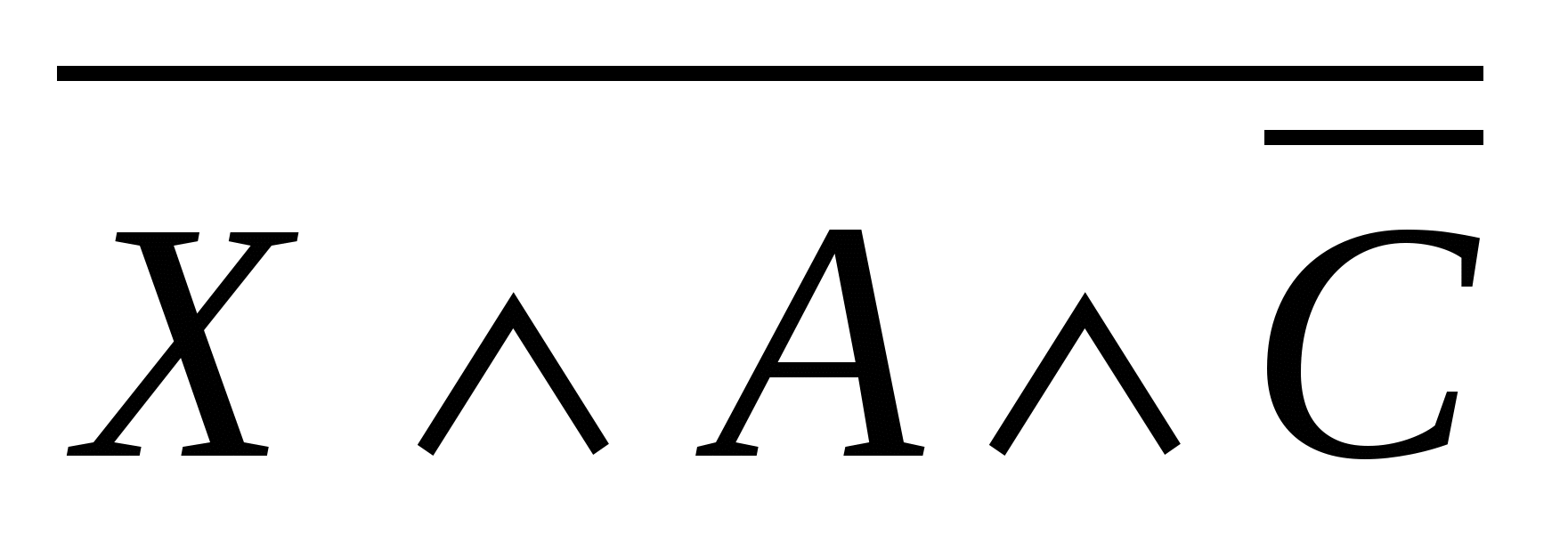 . .
Выявите логическую структуру высказываний и определите их значение истинности
число 5 – натуральное или не натуральное;
число 5 – натуральное и не натуральное;
7 < 3 или 7 3;
7 < 3 и 7 3;
Решите следующие задачи на распознавание объекта:
Среди данных чисел укажите нечетные 12, 45, 78, -5, 0.
Среди данных фигур укажите прямоугольные треугольники
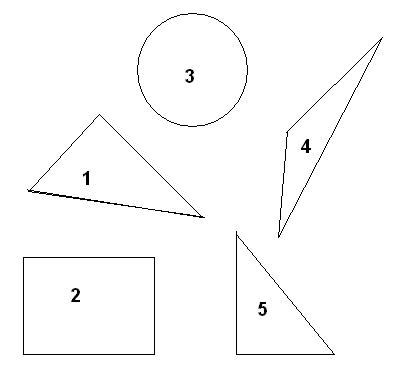
среди данных записей укажите уравнения: а +0 = а; 5+4=7; 5+7; а+ 1 = 0.
Приведите примеры определений, имеющих дизъюнктивную структуру. Приведите примеры определений, имеющих конъюнктивную структуру.
Практическое занятие 1.8. Высказывания с кванторами.
Вопросы и задания для подготовки к занятию:
Разбейте следующие предложения на две группы. По какому признаку Вы это сделали? Запишите эти предложения, используя обозначения.
Существуют четные числа;
Любое четное число оканчивается на 2;
Некоторые числа круглые;
Найдутся натуральные числа меньшие 5;
Для каждой пары натуральных чисел верно переместительное свойство сложения.
Lля доказательства каких из следующих утверждений необходимо провести рассуждения в общем виде, а для каких — достаточно привести пример?
в любом параллелограмме сумма величин противоположных углов равна 180°;
найдется ромб, диагонали которого равны;
в некоторых треугольниках все высоты делят противополож ную сторону пополам;
для любого натурального числа п имеет место неравенство п2+1=0;
существуют тупоугольные треугольники;
любое число, делящееся на 4, делится на 2.
все натуральные числа больше 2;
любая фигура имеет центр симметрии;
в некоторых треугольниках сумма внутренних углов больше 180°.
Запишите следующие высказывания:
все элементы множества Х обладают свойством Р;
некоторые элементы множества Х обладают свойством Р;
некоторые элементы множества Х не обладают свойством Р;
ни один элемент из множества Х не сбладает свойством Р.
Образуйте отрицания следугсщих высказываний:
некоторые глаголы отвечают на вопрос «что делать?»;
все однозначные числа больше 5;
существует натуральлое число, являющееся решением уравнения х + З = О;
некоторые геометрические фигуры являются многоугольниками;
любое дерево есть растение; с) каждый треугольник является равнобедренным;
по крайней мере одно из целых чисел превышает число 102;
Прочтите следующие записи, заменив символические обозначения кванторов общности и существования их словесными выражениями:
(х R) х2 -1 = (х + 1) (х - 1);
(у R) 5 + у = 5;
(у R) у + 3 > 0;
(х N) х + 3 < 0.
Задания для самостоятельной работы:
Укажите способы установления значения истинности высказываний, содержащих кванторы, заполнив таблицу:
Структура
высказывания
значение
истинности
|
(х Х) А(х)
|
(х Х) А(х)
|
И
|
|
|
Л
|
|
|
Установите, какие из нижеприведенных высказываний истинны, а какие ложны:
Во всяком четырехугольнике диагонали равны.
Существуют числовые выражения, значения которых нельзя найти.
При делении на 5 некоторых натуральных чисел в остатке получается 7.
Любое однозначное число является решением неравенства х + 2 > 1.
все треугольники подобны между собой;
некоторые равнобедренные треугольники являются прямоугольными;
все четные числа делятся на 8;
все числа, делящиеся на 8, четны.
Докажите или опровергните следующие высказывания:
Существуют уравнения, множество решений которых пусто.
Всякое целое число является натуральным.
Сумма любых двух четных чисел есть число четное.
Хотя бы одно натуральное число является решением уравнения 7:х = 2
Данные ниже высказывания взяты из учебников математики для начальных классов. Выясните, какие из них содержат (в явном или неявном виде) квантор и как следует устанавливать их значение истинности (указать только способ м обосновать его выбор):
От перестановки слагаемых сумма не изменяется.
Два соседних слагаемых можно заменять их суммой.
Площадь прямоугольника равна произведению его длины на ширину.
Существуют четные числа.
Некоторые числа делятся на 4.
Среди многоугольников есть треугольники.
Сформулируйте высказывания, которые являются отрицаниями данных высказываний. Для каждого из данных и полученных высказываний укажите, истинно само высказывание или его отрицание:
я вчера решил заданную на дом задачу;
все слова могут быть разделены на слоги;
один в поле не воин;
число 27 делится на 7;
3 плюс 6 равно 9;
253 —четное число;
Сформулируйте, используя законы де Моргана, отрицания следующих утверждений:
Четырехугольник ABCD - прямоугольник или параллелограмм.
Число 12 - четное и делится на 3.
Практическое занятие 1.9. Отношение следования и равносильности между предложениями. Структура теоремы. Виды теорем.
Вопросы и задания для подготовки к занятию:
Отношение следования между высказывательными формами.
Отношение равносильности между высказывательными формами.
Теорема и ее логическая структура.
Обратная теорема.
Противоположная теорема.
Закон контрапозиции.
На множестве Х = {2, 3, 4, 5, .6, 7, 8} заданы предикаты: А (х): «х  4» и В (х): «х 4» и В (х): «х  2». Найдите значения истинности высказываний А (а) и В (а) при каждом из значений а Х. На основании ответов, полученных выше выясните, истинно ли высказывание «из А (х) следует В (х)». Если да, то запишите этот факт, используя символ «». Можно ли утверждать, что истинно высказывание «Из В (х) следует А (х)»? Почему? 2». Найдите значения истинности высказываний А (а) и В (а) при каждом из значений а Х. На основании ответов, полученных выше выясните, истинно ли высказывание «из А (х) следует В (х)». Если да, то запишите этот факт, используя символ «». Можно ли утверждать, что истинно высказывание «Из В (х) следует А (х)»? Почему?
Известно, что высказывания: а) А (х) В (х), б) В (х) А (х) истинны. В каком отношении находятся множества ТА и ТВ?
На множестве Х = { 1, 2, 3, ..., 9} заданы предикаты А (х): «х > 2», В (х): «х > 5», С (х): «х - однозначное число». Сделайте соответствующие записи и докажите, что на множестве Х: а) предикат А (х) следует из предиката В (х); б) предикат С (х) следует из предиката А (х); в) из предиката В (х) следует предикат А (х).
Задания для самостоятельной работы:
В классе имеются два отличника: Попова и Смирнов - и пять спортсменов: Попова, Деменченко, Смирнов, Виноградов, 3иниченко. Следует ли предложение «Учащийся класса - спортсмен» из предложения «Учащийся класса -отличник»?
Докажите, что каждое из нижеприведенных утверждений ложно:
а) если треугольник равнобедренный, то он равносторонний;
б) если треугольник прямоугольный, то он равнобедренный;
в) если треугольник равнобедренный, то он остроугольный.
Сформулируйте следующие высказывания в виде «если ..., то ...»:
а) А - достаточное условие для В;
б) А - необходимое условие для В;
в) В - достаточное условие для А;
г) В - необходимое условие для А.
Среди следующих предложений укажите истинные; ответы обоснуйте:
а) Число п - натуральное, следовательно, и 15а - натуральное числе
б) Число 15а - натуральное, следовательно, а - натуральное число
в) Если в четырехугольнике все углы прямые, то этот четырехугольник - прямоугольник.
г) Если в четырехугольнике диагонали равны, то этот четырехугольник - прямоугольник.
д) Для того чтобы четырехугольник был прямоугольником, достаточно, чтобы все его углы были равны.
е) Для того чтобы четырехугольник был прямоугольником, необходимо, чтобы все его углы были равны.
Равносильны ли следующие предложения А (х) и В(х), если:
а) А(х) - «число делится на 9», В(х) - «сумма цифр в записи числа делится на 9».
б) А(х) - «каждое слагаемое суммы делится на 4», В(х) - «сумма делится на 4».
Докажите, что предложение «в прямоугольнике F диагонали взаимно перпендикулярны» и «прямоугольник F - квадрат» равносильны. Утверждения о равносильности сформулируйте тремя различными способами.
Вставьте слова «и» либо «или» так, чтобы следующие высказывания были истинными:
а) аb=0 a=0...b=0;
б) аb 0 а 0 ...b 0;
в) хА В хА…хВ;
г) хА В хА…хВ.
Какие из следующих предложений можно переформулировать, употребив слова «необходимо» либо «достаточно»:
а) Если в четырехугольнике все углы равны, то четырехугольник является прямоугольником.
б) Сумма двух четных чисел есть число четное.
в) Всякое число, которое делится на 3 и на 5, делится на 15.
Какие из нижеприведенных высказываний истинные:
а) Для того чтобы число делилось на 3, достаточно, чтобы оно делилось на 6.
б) Для того чтобы число делилось на 3, необходимо, чтобы оно делилось на 6
в) Для того чтобы число делилось на 100, необходимо и достаточно, чтобы оно делилось на 10.
г) Для того чтобы число делилось на 10, необходимо и достаточно, чтобы оно делилось на 2 и на 5.
В следующих теоремах выделите условие и заключение и сформулируйте их в виде: «если ..., то ...»:
а) во всяком треугольнике против конгруэнтных углов лежат конгруэнтные стороны,
б) перпендикуляр к одной из двух параллельных прямых есть также перпендикуляр к другой;
в) сумма величин углов треугольника равна 180°;
г) сумма величин смежных углов равна 180°;
д) параллелограмм имеет центр симметрии.
Выразите следующие теоремы без использования союзов «если ..., то...»:
а) если многоугольник правильный, то в него можно вписать окружность;
б) если две прямые перпендикулярны к одной и той же прямой, то они параллельны;
в) если стороны параллелограмма конгруэнтны, то его диагонали взаимно перпендикулярны.
Сформулируйте для каждой из этих теорем обратную, противоположную и обратную противоположной. установите, какие из этих теорем истинны.
Верна ли следующая теорема: если произведение двух целых чисел делится на 15, то хотя бы один из сомножителей делится на 15? Верна ли обратная теорема?
Для каждой из следующих теорем сформулируйте обратную, противоположную и обратную противоположной теоремы. Выясните, какие из этих теорем истинны:
а) если многоугольник правильный, то в него можно вписать окружность,
б) если сумма цифр какого-нибудь числа делится на 9, то это число делится на 3.
Пользуясь законом контрапозиции, докажите следующие теоремы:
а) Если р q - нечетное число, то р и q нечетны (р, q N).
б) Если п2 + т2 0, то т 0 или п 0.
Покажите, что следующие теоремы являются конъюнкцией двух теорем:
а) На 5 делятся те и только те числа, запись которых оканчивается цифрой 0 или цифрой 5.
б) Две прямые плоскости параллельны тогда и только тогда, когда они перпендикулярны одной и той же прямой.
в) для того чтобы в прямоугольном треугольнике катет составлял половину гипотенузы, необходимо и достаточно, чтобы угол, лежащий против этого катета, был равен 30°.
Практическое занятие 1.10. Умозаключения и их виды. Схемы дедуктивных умозаключений.
Вопросы и задания для подготовки к лекции:
Умозаключение и его структура.
Виды умозаключений:
дедуктивные умозаключения.
индуктивные умозаключения.
неполная индукция.
аналогия.
умозаключения от противного.
Схемы дедуктивных умозаключений.
Виды неправильных умозаключений.
Известно, что если в треугольнике углы при основании равны, то он – равнобедренный. Следует ли из этого, что: треугольник с двумя углами по 40˚ - равнобедренный; треугольник с двумя сторонами по 4 см – равнобедренный.
В четырехугольнике ABCD все стороны равны. Достаточно ли этого для того, чтобы утверждать, что ABCD: а) квадрат; б) ромб
Выяснив, что (12+4):2=12:2+4:2, ученик решил аналогично действовать при нахождении значения выражения (12*4):2, и записал: (12*4):2=(12:2)*(4:2). Прав ли он?
Даны два утверждения А(х) – «число х - четное»,В(х) – «запись число х заканчивается цифрой 4». Находятся ли они в отношении следования?
В каждом из следующих умозаключений выделите посылки и заключение:
если число натуральное, то оно целое; если число целое, то оно рациональное, следовательно,
если число натуральное, то оно рациональное; если число натуральное, то оно целое; число 138 – натуральное, следовательно, оно целое;
всякое натуральное число целое; число 138 – целое, следовательно, оно натуральное;
всякое натуральное число целое; число 0,2 не является целым, следовательно, оно не является натуральным.
Используя правило отрицания, закончите умозаключения так, чтобы они были дедуктивными:
если четырехугольник – прямоугольник, то в нем диагонали равны. Четырехугольник ABCD -…
равные треугольники имеют равные площади. Треугольники ABC и KLM -…
Восстановите общую посылку в умозаключении:
число 12 – натуральное, следовательно, оно положительное;
число 15 – нечетное, следовательно, оно не делится на 2.
|
 Скачать 387.5 Kb.
Скачать 387.5 Kb.






 тношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств.
тношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на рисунке. Покажите каждое из множеств. айти объединение и пересечение множеств А и В, если
айти объединение и пересечение множеств А и В, если