Урок математики Законы сложения 5 класс,УМК С.М.Никольский. Урок математики 5 класс ,Законы сложения, Хмура Т.А. Разработка урока по математике в соответствии с требованиями фгос по теме Законы сложения
 Скачать 109.03 Kb. Скачать 109.03 Kb.
|
|
Методическая разработка урока по математике в соответствии с требованиями ФГОС по теме «Законы сложения» Выполнила: Хмура Татьяна Алексеевна, учитель математики филиала МБОУ Жуковская СОШ №2 им.Е.П.Новикова в п.Олсуфьево Жуковка, 2020. АННОТАЦИЯ Методическая разработка содержит конспект урока и технологическую карту, разработанную в соответствии с современными требованиями Федерального государственного образовательного стандарта основного общего образования. Технологическая карта урока предназначена для проведения урока по математике в 5 классе по теме «Законы сложения ». Это первый урок при изучении данной темы. Материал будет полезен для учителей, работающих в 5-х классах, так как технологическая карта урока является современной формой планирования педагогического взаимодействия учителя и ученика, дающая возможность отразить деятельностную составляющую взаимодействия всех участников учебного процесса. Данный урок проводится в 5 классе по учебнику «Математика, 5», автор С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. Урок проводится в малокомплектной школе, в классе 7 учащихся. Тип урока: урок открытия новых знаний. Формы работы учащихся: фронтальная, индивидуальная. Дидактические приёмы: «графический диктант», «телеграмма», «птичий базар». Используемое оборудование: моноблок, учебники по математике. В соответствии с ФГОС на каждом этапе урока формируются определённые УУД. В технологической карте описаны деятельность и действия учителя и учащихся на каждом этапе. Методическая разработка содержит, в качестве приложения к технологической карте, задания к игре, дидактические карточки, маршрутные листы(листы самооценки) ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
КОНСПЕКТ УРОКА Эпиграф урока «В науке нет широкой столбовой дороги, и только тот может достигнуть её сияющих вершин, кто, не страшась усталости, карабкается по её каменистым тропам» К.Маркс. Девиз урока: «Дорогу осилит идущий, а математику – мыслящий» План урока 1. Организация начала урока. 2. Подготовка к основному этапу урока. Постановка темы и целей урока. 3. Усвоение новых знаний и способов действий. 4. Физкультминутка. 5. Первичная проверка понимания. 6. Подведение итогов урока. Рефлексия. 7. Информация о домашних заданиях, инструктаж по его выполнению. Ход урока 1. Организация начала урока. Здравствуйте ребята! Если день начинать с улыбки, то можно надеяться, что он пройдет удачно. Давайте сегодняшнее занятие проведем с улыбкой. Главная задача – быть внимательными, активными, находчивыми, а главное – трудолюбивыми. Математика, друзья, Абсолютно всем нужна. На уроке работай старательно, И успех тебя ждёт обязательно! Давайте настроимся на плодотворную работу и у нас всё получится. Я – умею мыслить и удивляться, обижаться и огорчаться Я – умею думать и понимать, слушать и отвечать Я – могу ошибаться Я – умею учиться Я – хочу учиться. «В науке нет широкой столбовой дороги, и только тот может достигнуть её сияющих вершин, кто, не страшась усталости, карабкается по её каменистым тропам» К.Маркс. Как вы понимаете эпиграф нашего урока? (только прилежные и трудолюбивые добьются успеха ) И сегодня девиз урока «Дорогу осилит идущий, а математику – мыслящий» Мы постараемся подняться с вами на горную вершину( в переносном, конечно, смысле) Горная вершина знаний – это цели нашего урока. У вас маршрутные листы (оценочные листы) (Приложение №1). Сможем ли мы достичь вершины (выполним ли цель урока)? 2. Подготовка к основному этапу урока.Постановка темы и целей урока. Перед тем как отправиться в путешествие нам надо собрать рюкзак. Положить в него снаряжение- знания, которые пригодятся нам в пути. I.Снаряжение . Фронтальный опрос. -Какая дробь называется обыкновенной? -Что означает числитель и знаменатель дробей? -Какая дробь называется правильной ? -Какая дробь называется неправильной? -Сократимая дробь – это … -Несократимая дробь - это … -Как сложить дроби с одинаковыми знаменателями? -Как сложить дроби с разными знаменателями? II.Графический диктант (Приложение №2)( ответы заносятся в маршрутный лист) Самопроверка по эталону. III.У подножия . Багаж знаний «Умею»,«Не умею»(Приложение №3) Но чтобы двигаться дальше нам надо определить тему урока(горную вершину)и цели нашего путешествия. IV. Наскальные рисунки. (Приложение № 4)(расшифровать) (Законы сложения, переместительный закон, сочетательный закон) Тема нашего урока - Законы сложения (запись в тетрадь). Давайте попытаемся сформулировать цели нашего урока (повторить законы сложения; доказать, что законы сложения переместительный и сочетательный применимы и для обыкновенных дробей; рассмотреть их применение при решении задач на вычисления). 3. Усвоение новых знаний и способов действий. А как вы думаете, применимы ли эти законы для обыкновенных дробей? У доски один учащийся решает пример с дробями( дроби придумывают ученики, знаменатель до 10) (остальные записывают в тетради) 2 +5 = 2+5= 5+2=5 + 2 9 9 9 9 9 9 Какой вывод можно сделать? (переместительный закон применим для обыкновенных дробей). Кто сможет записать закон в буквенном виде?(записывают на доске и в тетрадях) р + r= r+ p q q q q Сформулируйте переместительный закон(приём «Птичий базар» - хоровое произношение). А теперь докажем, что сочетательный закон применим и для обыкновенных дробей. У доски один учащийся, остальные записывают в тетрадь(дробь придумывают ученики, знаменатель до 5) (1 + 3 ) + 2 = 1+3 + 2 =(1+3) +2 = 1+(3 +2 )= 1 + 3+2 = 1 + ( 3 + 2) 5 5 5 5 5 5 5 5 5 5 5 5 Какой вывод можно сделать? (сочетательный закон применим для обыкновенных дробей). Кто сможет записать закон в буквенном виде? (записывают на доске и в тетрадях) (p + r ) + m = p + ( r + m) q s n q s n Теперь узнаем, правильно ли мы сформулировали законы сложения. Проверить гипотезу с помощью учебника стр.188-189. Что нового ещё узнали? (Из законов сложения следует, что сумму нескольких дробей можно записывать без скобок; любые слагаемые в ней можно менять местами и заключать в скобки, этим пользуются для упрощения выражений) Чтобы двигаться дальше, нам надо немного отдохнуть. 4. Физкультминутка. Поднимает руки класс – это раз, Повернулась голова – это два, Руки вниз, вперёд смотри - это три, Руки в стороны пошире развернули на четыре, С силой их к плечам прижать – это пять, Всем ребятам тихо сесть – это шесть. 5.Первичная проверка понимания. Проверим применение законов на примерах. Учебник стр. 189 № 847,№848(а, б, в) (фронтально) №849,№850,852 а – на доске (взаимопроверка), б – с комментированием, в – самостоятельно (самооценка) Фронтально. Выберите закон сложения, который можно применить в данном случае(поднимите ручку или карандаш)(ручка - переместительный закон, карандаш – сочетательный закон, ручка и карандаш – переместительный и сочетательный законы). (2 +5) + 8 = 17 17 17 4 + 2 + 6 = 21 21 21 2 + 7 + 1 = 49 49 49 6.Подведение итогов занятия. Рефлексия. Достигли ли мы с вами вершины (цели урока)? Доказали, что законы сложения применимы и для обыкновенных дробей? Можете сформулировать законы сложения ? Научились применять эти законы при решении примеров? Для чего, с какой целью рассматриваются эти законы? (Чтобы быстрее и удобнее найти значение выражений в целях экономии времени) По маршрутным листам оцените себя: кто достиг вершины? кому нужна помощь? Ваша итоговая оценка? Обсуждение (самооценка,взаимооценка). В чём трудность? (если есть) Причина неудачи? (если плохой результат). Чтобы вы себе пожелали по изученной теме запишите (приём «телеграмма» ) Выскажите своё мнение «сегодня на уроке» и оценить успешность своей деятельности (расположить человечка на соответствующей ступеньке лестницы)(Приложени№5) Я –повторил… Я- закрепил … Я- узнал … Я –научился… 7.Информация о домашнем задании, инструктаж о его выполнении. Читать п.4.7.стр.188-189,выучить формулировки законов сложения, выполнить на выбор №№850(г,д,е,),852(г,д,е) или №№ 851(б,в),853(а,б,в) При выполнении внимательно читайте задание, не забывайте ,что в ответе должна быть несократимая дробь. Выставление оценок в дневник. Рада была с вами пообщаться, до свидания. ЗАКЛЮЧЕНИЕ В современном образовательном процессе все более актуальным становится использование в обучении приемов и методов, которые формируют умения самостоятельно добывать знания, собирать необходимую информацию, выдвигать гипотезы, делать выводы и умозаключения. А это значит, что у современного ученика должны быть сформированы универсальные учебные действия, обеспечивающие способность к организации самостоятельной учебной деятельности. Урок «Законы сложения» первый урок из 4 уроков по данной теме. Урок связан с предыдущими уроками по теме «Приведение дробей к общему знаменателю»,«Сложение дробей». Полученные на уроке знания и умения будут работать на последующие уроки данной темы. При подготовке к уроку были учтены программные требования ФГОС: соответствие целей и задач урока по новым стандартам и программе темы «Законы сложения»;на уроке использованы различные виды деятельности (фронтальный опрос, коллективная работа, индивидуальная и самостоятельная работа); воспитание культуры математической речи, умения высказывать свою точку зрения, слушать других, принимать участие в диалоге; структура урока соответствует структуре урока изучение новых знаний . Уникальность этого урока - развивать умения работать с текстом (внимательно читать, выделять главное), анализировать, сравнивать, делать выводы, развивать внимание и память, познавательный интерес через игровые моменты, взаимопроверку и самопроверку. Тип урока выбран в соответствии с требованиями образовательного стандарта и особенностями преподавания уроков математики. Были учтены особенности учащихся при подготовке к уроку: умение работать в группах; способность к позитивному сотрудничеству. На уроке решались задачи по формированию УУД: предметные: - умение применять правила сложения дробей, выполнять сложение удобным способом, умение оперировать математической логикой, совершенствование практических навыков вычисления; метапредметные:- умение применять знания на практике ,умение осуществлять анализ с выделением признаков, умение работать с информацией, умение оценивать продукт своей деятельности. коммуникативные: - умение выслушивать мнение одноклассника и сопоставлять его со своим, выдвигать гипотезу, умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, воспитывать ответственность и аккуратность. регулятивные: - проявлять ответственность за собственный выбор и результаты своей деятельности, способность к рефлексии собственной деятельности и деятельности своих товарищей. познавательные: - строить рассуждения на основе сравнения, выделяя общие признаки, излагать полученную информацию, интерпретируя её в контексте решаемой задачи; личностные: - самостоятельность; самооценка, ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи. Управление учебной деятельностью школьников осуществлялось путем взаимоконтроля и самоконтроля, инструктажа и помощи учителя. На уроке удалось решить поставленные задачи урока и получить соответствующие им результаты обучения; избежать перегрузки и переутомления учащихся; удалось полностью реализовать все поставленные задачи; выполнены все планируемые задания; пройдены все этапы урока. Данный урок позволил включить всех обучающихся в активную работу, обеспечить каждому обучающемуся посильное участие в решении проблем. В процессе работы у обучающихся формируются коммуникативные навыки, способность к сотрудничеству и взаимодействию, развивается критическое мышление, что является необходимым для их социализации СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ 1.Федеральный закон "Об образовании в Российской Федерации" N 273-ФЗ от 29 декабря 2012 года с изменениями 2017-2016 года 2.Федеральные государственные образовательные стандарты ООО 3.Математика. 5 класс: учебник для общеобразоват. учреждений / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2016; 4.Математика. Дидактические материалы. 5 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2009–2012; 6.Математика. Рабочая тетрадь. 5 класс. В двух частях / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2012; 7.Математика. Тематические тесты. 5 класс / П. В. Чулков, Е. Ф. Шершнев, О.Ф. Зарапина. — М.: Просвещение, 2009–2012 Приложение №1 Маршрутный (оценочный )лист.
Приложение №2 Графический диктант.(да - ^, нет – v) 1. 5 - правильная дробь. 8 2. 11 - несократимая дробь. 22 3. 7 - несократимая дробь. 15 4. 12- правильная дробь. 19 5. 28 - неправильная дробь. 29 6. Числитель и знаменатель несократимой дроби – взаимно-простые числа. 7. Из двух дробей с одинаковыми знаменателями больше та, у которой числитель меньше. 8. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. Ответы
Эталон ответов
Приложение 3 Таблица «Багаж знаний»
Приложение №4 Таблица «Наскальный рисунок»
Приложение № 5 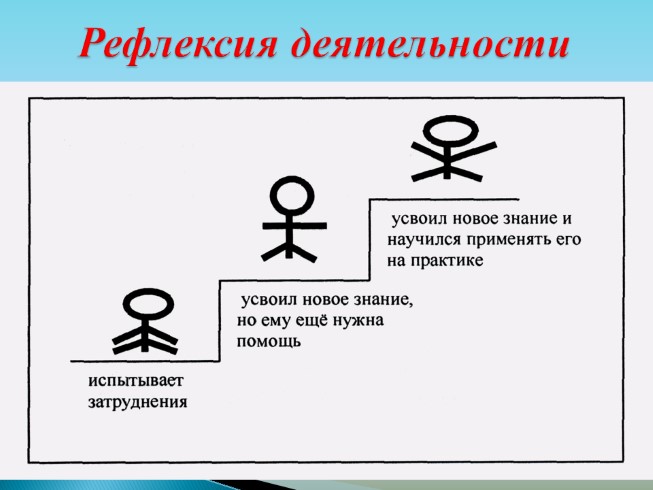 ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
|
