Курсовая. Трипузова К.Д. 2 курс, МО. Приближенное решение алгебр. Решение алгебраических уравнений. 1 Метод хорд или способ линейной интерполяции

• Название: Решение алгебраических уравнений. 1 Метод хорд или способ линейной интерполяции
• Дата: 27.12.2021
• Размер: 437.31 Kb.
• Имя файла: Курсовая. Трипузова К.Д. 2 курс, МО. Приближенное решение алгебр.docx
• Тип: Решение; #319434

Содержание

1. Введение.

2. Приближённое решение алгебраических уравнений.

2.1 Метод хорд или способ линейной интерполяции.

2.2 Метод касательных или способ Ньютона.

2.3 Комбинированный метод. Комбинированное применение способов хорд и касательных.

3. Заключение.

4. Список литературы.

1. 
   Введение.
   

Известно, что квадратные уравнения решали уже и в античной Греции, но способы решения алгебраических уравнений третьей и четвертой степени были открыты только в XVI веке. Эти традиционные методы дают точные значения корней и выражают их через коэффициенты уравнения с помощью радикалов всевозможных степеней. Впрочем, эти способы приводят к долгим и громоздким вычислениям и вследствие этого почти не имеют практической ценности.

Что касается алгебраических уравнений пятой и высших степеней: доказано, что в общем случае их решения не выражаются через коэффициенты с помощью радикалов.

Впрочем, это не значит, что в науке нет методов решения уравнений высших степеней. Существует большое количество методик приближенного решения уравнений – алгебраических и неалгебраических (иначе – трансцендентных), которые позволяют вычислять их корни с любой степенью точности, подходящей для конкретных практических целей.

К примеру, при помощи графика или же каким- либо другим способом, как правило, удается установить приближенные значения корней. Это позволяет для всякого корня получить грубые приближения по недостатку и по избытку. Таких грубых приближений часто бывает достаточно, чтобы, отталкиваясь от них, получить в итоге все значения корня с той точностью, которая потребуется.

Об этом и пойдет речь.

2. 
   Приближенное решение алгебраических уравнений.
   

Рассмотрим некоторые методы численного решения уравнений вида

f(x) = 0,

где f(x) – заданная алгебраическая или трансцендентная функция действительного аргумента x; в первом случае уравнение называется алгебраическим, во втором – трансцендентным.

Не каждое уравнение удается решить точно, и, прежде всего, это относится к большинству трансцендентных уравнений. Известно также, что нельзя точно решить произвольное алгебраическое уравнение пятой степени и выше. Но, поскольку точное решение уравнения в большинстве случаев не требуется, считают, что задача отыскания корней решена, если их значения определены с требуемой степенью точности.

Поставленная задача выглядит следующим образом:

Дано уравнение f(x) = 0, где f(x) – непрерывная функция в некоторой области. Корни этого уравнения x* - значения аргумента x, которые обращают уравнение в верное равенство. Найти приближенное значение корня x* с точностью ε означает указать интервал длиной не более ε, содержащий точное значение корня x.

Чтобы найти приближенные значения корней уравнения нужно решить две задачи:

1)отделение корней, т.е. выделение интервалов из области непрерывности функции, в каждом из которых заключен только один корень уравнения;

2)уточнение корня, т.е. построение итерационного процесса, позволяющего сузить границы выделенного интервала до значения заданной точности.

2.1.Метод хорд или способ линейной интерполяции.

Этот метод нахождения простых корней широко применяется при решении конечных уравнений. Другие названия рассматриваемого метода: метод ложного положения, метод линейной аппроксимации, метод пропорциональных частей, метод секущих.

Идея метода хорд состоит в том, что на достаточно малом промежутке  дуга кривой y=f(x) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Ox, т.е. это точка x=c.

Пусть дано уравнение  , где -непрерывная функция, имеющая в интервале производные первого и второго порядков. Корень считается отделенным и находится на отрезке , т.е. .

Существуют четыре случая расположения дуги кривой, учитывая значения первой и второй производных: прил.1, прил.2.

Рассмотрим случай, когда первая и вторая производные имеют одинаковые знаки, т.е.  .

Пусть, например,  График функции проходит через точки . Искомый корень уравнения есть абсцисса точки пересечения графика функции с осьюOx. Эта точка нам не известна, но вместо нее возьмем точку с пересечения хорды с осью Ox. Эта точка x₁=c является приближенным значением корня.

Уравнение хорды, проходящей через точки А₀ и В имеет вид:



а абсцисса ее точки пересечения x₁=c с осью Ox (т.е. когда  ) определяется формулой:



Очевидно, что точка x₁=c обязательно окажется внутри отрезка  , при этом она будет тем ближе к искомому корню, чем меньше кривизна графика функции, а так как кривизна определяется формулой:



Точка x₁=c будет тем ближе к некому корню  , чем меньше и чем больше на отрезке .

Замечание Хорда всегда расположена со стороны вогнутости дуги графика и, как видно из приведенных выше рисунков, точки x₁=c всегда ближе точки x₀ к тому концу отрезка  , в котором знак функции противоположен знаку ее второй производнойf’’(x).

Пример 1

Методом хорд уточнить корень уравнения  отделенный на отрезке .

Решение

Имеем  = ,f’(x)=3x²-1, f’’(x)=6x. Так как на отрезке  , то точкаx₁=c будет левым концом нового отрезка  ;



Отметим, что приближенное значение с взято с недостатком, т.к. с₀ и при округлении с избытком есть опасность «перешагнуть» через корень x₀. В качестве отрезка  для дальнейшего уточнения следует взять [1,1;2].

Если значение приближенного корня x1 не устраивает, его можно уточнить, применяя метод хорд к отрезку  . Соединив точкуA₁(x₁,f(x₁)) с точкой B(b,f(b)) находим x₂ – точку пересечения хорды с осью Ox:



Продолжая этот процесс, находим:

и вообще 

Процесс продолжается до тех пор, пока не получим приближенный корень с заданной степенью точности.

По приведенным выше формулам вычисляются корни и для случая, когда 

Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е.  .

Пусть, например,  В этом случае соединив точки , имеем уравнение хорды, проходящей через A и B_0:



Найдем x₁ как точку пересечения хорды с осью Ox, полагая y=0:



Корень теперь заключен внутри подотрезка  .

Применяя метод хорд к отрезку  , получим:

и вообще 

По этим же формулам находится приближенное значение корня и для случая, когда 

С учетом сделанного выше отметим, что выбор тех или иных формул метода хорд обуславливается правилом – неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком ее второй производной.

Так, если  , то неподвижен конец b, а все приближения к корню x₀ лежат со стороны конца a; если же  , то неподвижен конец a, а все приближения к корню x₀ лежат со стороны конца b.

При оценке погрешности приближения пользуются формулой: , где - точное значение искомого корня, а и -приближения к нему, полученные на(n-1) и n-м шагах.

Эта формула применима, если выполнено условие  где

Пример 2

Методом хорд уточнить до  меньший корень уравнения , отделенный на отрезке [-3,-2].

Решение

Проверим выполнимость условия  , учитывая что , .

Возьмем середину отрезка [-3,-2], т.е. точку x=-2,5, и выберем интервал [-3,-2,5]. Снова проверим условие  :

.

Теперь возьмем середину отрезка [-3,-2,5], т. е. точку x=-2,75.

На суженном отрезке [-2,75;-2,5] сохраняется условие монотонности функции (условие  ). Действительно, f(-2,75)=-2,75³+3*2,75²-3<0; f(-2,5)=-2,5³+3*2,5²-3>0;

т.е. 6,189<2*3,75.

Таким образом, для оценки погрешности корня, лежащего на отрезке [-2,75;-2,5], можно пользоваться формулой  , т.е. процесс последовательного приближения к корню следует продолжать до тех пор, пока не будет выполнено условие .

Определим знак второй производной f’’(x) и установим, какой конец отрезка будет неподвижным при использовании метода хорд. Находим f’’(x)=6x+6 и  . Значит, за неподвижный конец отрезка нужно принимать x=-2,75, а вычисление вести по формулам:  и ,

где a=-2,75; f(a)=-1,1019.

Если последнее выражение представить в виде:  , то сразу же можно будет получать разность между двумя последовательными приближениями и производить проверку на окончание вычислений, т.е. проверять выполнение неравенства:



Все результаты сведем в таблицу: прил.3

Из этой таблицы следует, что  , поэтому, округляя x³ до тысячных долей, получаем  .


2.2 Метод касательных или способ Ньютона.

Пусть корень уравнения  отделен на отрезке , причемf’(x) и f’’(x) и сохраняют постоянные знаки на всем отрезке  .

Геометрический смысл метода Ньютона состоит в том, что дуга кривой  заменяется касательной к этой кривой (отсюда и второе название метода - «метод касательных»).

Рассмотрим два случая:

а)  или

(прил.4)

Проведем касательную к кривой  в точкеB₀ (b,f(b)) и найдем абсциссуточки пересечения касательной с осью Ox. Известно, что уравнение касательной в точке B₀ (b,f(b)) имеет вид: 

Поскольку в нашем случае y=0, x=x₁,то получаем:  .

Теперь корень уравнения находится на отрезке [a,x₁]. Применяя снова метод Ньютона, проведем касательную к кривой в точке B₁ (x₁,f(x₁)) получим:  , и вообще: . Очевидно, что каждый следующий член последовательности есть более близкое приближенное значение к корню , чем предыдущий. Однако все в этом случае остаются больше истинного значения корня , т.е. - приближенное значение корня с избытком.

б)Пусть  или , т.е.

(прил.5)

Если снова провести касательную к кривой  в точке B_, то она пересечет ось абсцисс в точке, не принадлежащей отрезку  . Потому проведем касательную в точкеA₀(a,f(a)) и запишем ее уравнение 

Поскоку y=0, x=x₁,то получаем:  .

Очевидно, корень  находится на отрезке [x₁,b]. Повторив процедуру в точке A₁ (x₁,f(x₁)), получаем:  и вообще .

Итак, получив последовательность  приближенных значений искомого корня , отметим, что каждый последующий член ее ближе к истинному корню , чем предыдущий. Отсюда следует, что - приближенное значение корня с недостатком.

Анализ полученных формул в случае а) и в случае б) приводит к следующему правилу выбора начального приближения  корня :

-за исходную точку  следует брать тот конец отрезка , в котором знак функции совпадает со знаком второй производной f’’(x). Очевидно, в первом случае (случае а))  и начальная точка , а во втором случае и начальное приближение есть .

Примечание

1. 
   Для оценки погрешности приближенного значения корня  будем пользоваться формулой: , где (эта формула используется в методе хорд).
   
2. 
   В том случае, когда отрезок  настолько мал, что на нем выполняется условие , где , точность приближения на n-ом шаге оценивается следующим образом: если  .
   
3. 
   Если производная f’(x) мало меняется на отрезке  , то для упрощения вычислений можно пользоваться формулой: , т.е. значение производной в начальной точке достаточно вычислить только один раз. Геометрически это означает, что касательные в точке B_n (x_n,f(x_n)) заменяются прямыми, параллельными касательной, проведенной к кривой  в точкеB₀(x₀,f(x₀)).
   

Пример 1

Методом касательных уточнить до  корень уравнения , расположенный на отрезке [-2,75;-2,5] .

Решение

Имеем : f(-2,75)=-2,75³+3*2,75²-3<0, f’’(x)=6x+6<0,  , т.е. .

Это означает, что вычисления надо вести по формуле  . Находим:f’(x)=3x²+6x, f’(x₀)=f’(-2,75)=(-3)*2,75*(-2,75+2)=6,1875.

Для удобства все вычисленное сведем в таблицу:

(прил.6)

Из этой таблицы следует, что  и поэтому корень

2.3 Комбинированный метод. Комбинированное применение способов хорд и касательных.

Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, и уточнение корня происходит быстрее.

Пусть дано уравнение  , корень отделен и находится на отрезке . Применим комбинированный метод хорд и касательных с учетом типа графика функции.

Если  , то метод хорд дает приближение корня с недостатком, а метод касательных – с избытком (прил.7)

Если же  , то методом хорд получаем значение корня ч избытком, а методом касательных – с недостатком (прил.8)

Однако, во всех случаях искомый корень  заключен между приближенными корнями, получающимися по методу хорд и по методу касательных, т.е.

выполняется неравенство: , где - приближенное значение корня с недостатком, - с избытком.

Вычисления следует вести в таком порядке:

-если  , то со стороны конца a лежат приближенные значения корня, полученные по методу хорд, а со стороны конца b – значения, полученные по методу касательных, и тогда:  ; .

Поскольку теперь искомый корень  находится на отрезке , то, применяя к этому интервалу комбинированный метод, получаем: ; и вообще: ; .

-если же , то со стороны конца a лежат приближенные значения корня, полученные по методу касательных, а со стороны конца b – значения, полученные по методу хорд, и тогда:  ; .

Комбинированный метод очень удобен при оценке погрешности вычислений. Процесс вычислений прекращается, как только станет выполняться

неравенство:  .

За приближенное значение корня следует принять  , где - приближенное значение корня с недостатком, - с избытком.

Пример 1

Комбинированным методом хорд и касательных уточнить до  корни уравнения .

Решение

1. 
   отделим корни аналитически. Имеем:  , , т.е. корни производнойx₁=-4, x₂=2.
   

Составим таблицу знаков функции: (прил.9)

Данное уравнение имеет три действительных корня:  .

Уменьшим промежутки нахождения корней до длины, равной 1: (прил. 10)

Итак,  .

2)уточним комбинированным методом хорд и касательных корень, лежащий в интервале (-7;-6).

Имеем f(-7)=-27<0, f(-6)=37>0 и  , , . Это означает, что применяем формулы: ; . Здесьa₀=-7, b₀=-6. Вычисления

сведем в таблицу: (прил.11)

Из таблицы следует, что 

3) Определим  Имеем f(0)=1>0, f(1)=-19<0 и  , , . Как и в случае нахождения (воспользовавшись теми же формулами, но в которыхa₀=0, b₀=1), строим таблицу для уточнения искомого корня. В результате получаем  .

4) Для уточнения приближенного корня комбинированным методом хорд и касательных на интервале (3;4) имеем: f(3)=-17<0, f(4)=7>0 и  , , .

Расчетные формулы в этом случае следующие:  ; . Построив таблицу последовательных вычислений, находим, что .

Приложения

Прил.1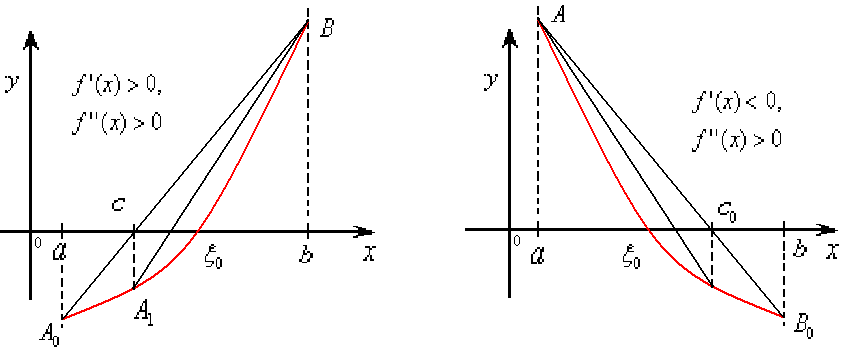



Прил.2



Прил.3

n	xn			3	f(xn)	xn-a
0	-2,5	-15,625	6,250	18,75	0,125	0,25	-0,025
1	-2,525	-16,098	6,3756	19,1268	0,0288	0,225	-0,006
2	-2,531	-16,213	6,4060	19,2180	0,0050	0,219	-0,0009
3	-2,5319

Прил.4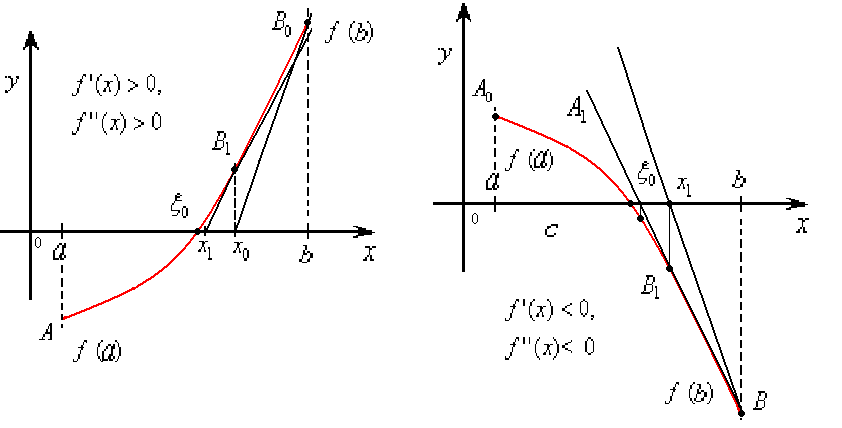



Прил.5



Прил.6

n	xn	-sin xn
0	1,178	-0,92384	0,00416	0,61723	-0,0065
1	1,1715	-0,92133	0,00017	0,01123	-0,0002
2	1,1713	-0,92127	0,00003	0,61110	-0,00005
3	1,17125

Прил.7



Прил.8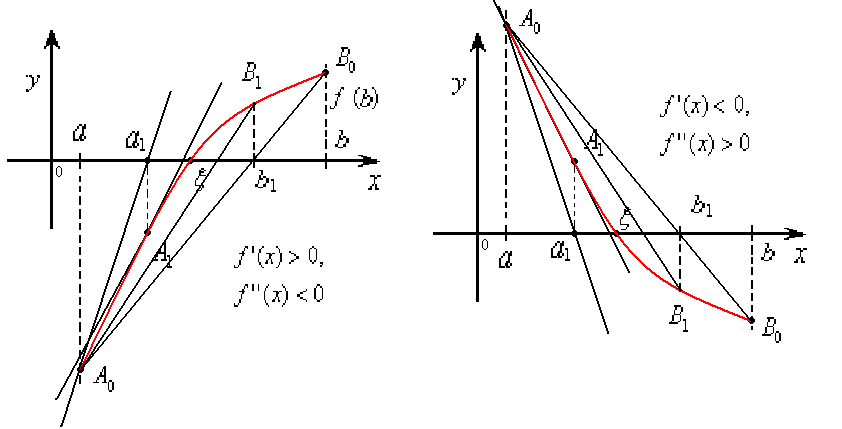



Прил.9

x	-∞	-4	2	+∞
sign f(x)	-	+	-	+

Прил.10

x	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4
sign f(x)	-	+	+	+	+	+	+	+	-	-	-	+

Прил.11