трехфазный генератор. Трехфазный генератор. Решение Для того чтобы рассчитать синхронный генератор. Необходимо определить расчетную мощность генератора, фазные токи, напряжения и коэффициент мощности
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Задание Трехфазный синхронный генератор с нерастянутыми полюсами имеет полную мощность SN = 900 000 кВА, активную мощность PN = 720 000 кВт, фазное напряжение U1N = 13 800 В, рассеянное индуктивное сопротивление обмотки статора 0,04 Ом, синхронное индуктивное сопротивление 0,57 Ом. Построить векторную диаграмму и определить значение ЭДС холостого хода, угол нагрузки θ и перегрузочную способность. Решение: Для того чтобы рассчитать синхронный генератор. Необходимо определить расчетную мощность генератора, фазные токи, напряжения и коэффициент мощности. У синхронных генераторов применяем cosφ= 0,8 , тогда: 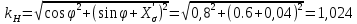 хσ -Индуктивное сопротивление рассеяния обмотки статора. ЭДС холостого хода, при естественной стабилизации напряжения:  Перегрузочная способность определяеься по формуле 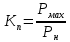  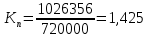 Построим упрощенную векторную диаграмму. Зависимость изменения напряжения от нагрузки генератора удобно выяснять с помощью векторных диаграмм синхронного генератора. Рассмотрим случай часто встречающий на практике,-случай активно-индуктивной нагрузки.  Рисунок 1 Упрощенная векторная диаграмма Построение векторной диаграммы начнем с произвольного расположения вектора ЭДС Е. От этого вектора под углом сдвига фаз ψ отложим вектор тока I Поскольку в соответствии с векторным уравнением электрического равновесия синхронного генератора напряжение U на величину индуктивного падения напряжения IXL, по этому для построения вектора напряжения U отложим от концавектора ЭДС Е перпендикулярно вектору тока I вектор падения напряения IXL. Соединив точку О с концом вектора IXL, получим вектор напряжения U на зажимах генератора. Полученный угол φ между векторами I и U определяет характер нагрузки. Постоянные по величине вращающиеся магнитные потоки ротора и статора можно заменить переменными потоками, изменяющиеся по тому же синусоидальному закону, что и создаваемые ими ЭДС и токи, по этому на этой же диаграмме можно построить магнитные потоки ротора, статора и резульирующий магнитный поток генератора. Магнитный поток полюсов Фр индуцирующий ЭДС Е, отстает от ЭДС по фазе на четверть периода, а поток стотара Фс, созданный током нагрузки I, совпадает с ним по фазе. Построив векторы Фр и Фс, можно получить вектор результирующего потока Ф из устловия Ф=Фр+Фс Векторные диграммы для различных нагрузок показывают, что изменения напряжение на зажимах генератора U и результирующего магнитного потока Ф зависят не только от внутреннего индуктивного падения напряжения IXL, и магнитного потока статора Фс, но и от характера нагрузки. Так, при активной и активно-емкостной нагрузке машина размагничивается, а при активно-емкостной–подмагничивается, что приводит к соответствующим изменениям ЭДС и напряжения на зажимах генератора. Так как по заданию нет данных о нагрузке генератора тогда считаем, что генератор работает вхолостую. Векторная диаграмма примет следующий вид:  Рисунок 2 Векторная диаграмма холостого хода генератора. При работе генератора вхолостую приемники отключены, и втогда следуею считать что Zn=∞. В этом случае I=0, по этому IXL=0, U=E, Ф=Ф0. Соответственно ϴ угол нагруки равен 0. |
