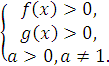№
|
Этапы урока
|
Задачи этапа
|
Деятельность учителя
|
Деятельность учащихся
|
УУД
|
1.
|
Организационный этап
|
Создать благоприятный психологический настрой на работу
|
Я хочу начать урок со словфранцузского писателя Анатоля Франца «Учиться можно только весело…Чтобы переваривать знания, надо поглощать их с аппетитом»
Давайте же и мы последуем совету писателя, и будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они скоро вам понадобятся при сдаче ЕГЭ.
Перед вами стоит задача – повторить способы и приёмы решений логарифмических уравнений
|
Включаются в деловой ритм урока
|
Личностные: самоопределение.
Регулятивные: целеполагание.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
|
2
|
Актуализация и фиксирование индивидуального затруднения пробном учебном действии.
|
Актуализация опорных знаний и способов действий.
|
Учитель: Скажите, что такое логарифм. Для того, чтобы было легче решать уравнения, вы должны уметь вычислять логарифмы. (слайд с устными упражнениями)
|
Отвечают на вопросы учителя. Вычисляют устно логарифмы
|
Коммуникативные: планирование учебного сотрудничества с учителем и сверстником.
Познавательные.
|
3
|
Целеполагание и мотивация
|
Обеспечение мотивации учения детьми, принятие ими целей урока.
|
(Слайд с уравнениями) Учитель: У вас на партах лежат памятки с методами решений логарифмических уравнений . Как вы думаете можно ли логарифмические уравнения решать одним способом? Какая цель нашего урока?
|
Учащиеся по памяткам повторяют изученные на предыдущих уроках методы решений логарифмических уравнений
|
Регулятивные: целеполагание.
Коммуникативные: постановка вопросов.
Познавательные: самостоятельное выделение-формулирование познавательной цели; логические - формулирование проблемы.
|
4
|
Закрепление знаний и способов действий
|
организация деятельности уч-ся по отработке изученных знаний и способов действий посредством их применения в ситуациях по образцу и измененных ситуациях
|
Итак, тема урока «Решение логарифмических уравнений»
Рассмотрите первый метод «По определению». Из предложенных уравнений (слайд с уравнениями) выберете те, которые решаются этим методом и решите.
Аналогично рассматриваются все методы решения.
|
Из предложенных уравнений выбирают подходящие под определённый метод и решают у доски и в тетради
|
Коммуникативные: постановка вопросов, инициативное сотрудничество.
Познавательные: самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство.
Регулятивные: планирование, прогнозирование.
|
5
|
Организация первичного контроля
|
Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.
|
Учитель: А теперь я предлагаю вам пройти тестирование Карточки с заданиями.
По окончанию учитель на экран выводит результаты каждого. Разбирают ошибки.
|
Каждый ученик проходит тестирование
|
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;
Личностные: самоопределение.
|
6
|
Углубление изученной темы.
|
Установление правильности и осознанности изучения темы.
Выявление пробелов изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы при подготовке к ЕГЭ.
|
Учитель: Предлагаю перейти к логарифмическим уравнениям, с чем вам придётся иметь дело на ЕГЭ по математике повторение теоретического материала.
|
Учащийся у доски решает традиционным способом
|
Регулятивные: контроль, оценка, коррекция.
Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач.
Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера.
|
7
|
Подведение итогов урока.
|
Дать качественную оценку работы класса и отдельных обучаемых
|
-Что изучили сегодня на уроке?
-С какими новыми методом мы познакомились?
Оценить учащихся
На следующем уроке мы рассмотрим применение метода рационализации при решении логарифмических неравенств. Этот метод широко применяется при решении неравенств разных видов, при решении экзаменационного материала типа С3. применение этого метода при решении показательных неравенств и иррациональных.
|
|
Регулятивные: оценка-осознание уровня и качества усвоения.
|
8
|
Информация о домашнем задании
|
Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.
|
Задание дается из книги «Математика ЕГЭ 2020» или на сайте www.alexlarin.narod.ru
СДАМ ГИА: РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня, Курс Д. Д. Гущина
|
|
|
9
|
Рефлексия
|
Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.
|
Если вы считаете, что поняли тему урока, то наклейте розовый листочек на прямоугольник.
Если вы считаете, что не достаточно усвоили материал, то наклейте голубой листочек.
Если вы считаете, что не поняли тему урока, то наклейте желтый листочек.
|
|
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;
Познавательные: рефлексия.
|
 Скачать 94.5 Kb.
Скачать 94.5 Kb.