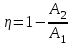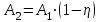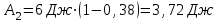101. Точка движется по окружности радиусом R= 4 м. закон ее движения выражается уравнением 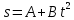 , где А=8 м, В= -2 м/с2. Определить момент времени, когда нормальное ускорение , где А=8 м, В= -2 м/с2. Определить момент времени, когда нормальное ускорение 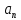 точки равно точки равно 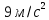 . Найти скорость . Найти скорость 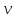 , тангенциальное , тангенциальное 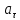 и полное и полное 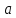 ускорение точки в тот же момент времени. ускорение точки в тот же момент времени.
Дано
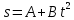
R= 4 м
А=8 м, В= -2 м/с2
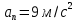
Найти: 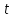 -?; -?;
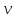 -?; -?; 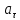 - ?; - ?; 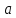 - ? - ?
|
Решение
Нормальное ускорение точки при движении по окружности
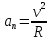
где 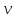 - скорость точки; - скорость точки;
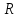 - радиус окружности. - радиус окружности.
Скорость точки
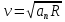
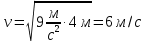
Уравнение изменения скорости точки определим через производную от пути
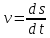
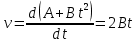
Время, когда нормальное ускорение равно 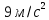 , определим из значения скорости в этот момент , определим из значения скорости в этот момент
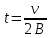
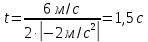
Тангенциальное ускорение
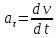
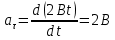
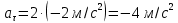
Полное ускорение
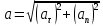
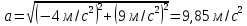
Ответ: 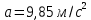 ; ; 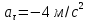 ; ; 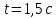 ; ; 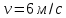
|
111. Тело скользит по наклонной плоскости, составляющей с горизонтом угол α=45°. Пройдя путь s = 36 см, тело приобретает скорость v=2 м/с. Найти коэффициент трения f тело о плоскость.
Дано
α=45°
s = 36 см=0,36 м
v=2 м/с
найти
f - ?
|
Р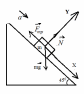 ешение ешение
По второму закону Ньютона силы, действующие на тело удовлетворяют выражению
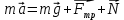 (1) (1)
Спроецировать на оси координат
ОХ: 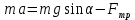 (2) (2)
ОУ: 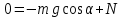 (3) (3)
Сила трения равна 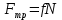 (4) (4)
Подставим уравнение (3) в (2) с учетом (4)
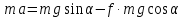
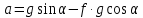
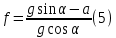
путь при равноускоренном движении 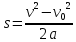
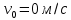
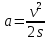
Подставим в (5)
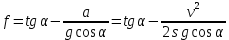
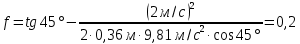
Ответ: 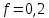
|
141. Налетев на пружинный буфер, вагон массой m=15 т, двигавшийся со скоростью v=0,7 м/с, остановился, сжав пружину на Δl=7 см. Найти общую жесткость k пружин буфера.
Дано
m=15 т=15000 кг
v=0,7 м/с
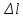 =7 см=0,07 м =7 см=0,07 м
Найти
k – ?
|
Решение
Движущийся ванном обладает кинетической энергией
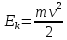
Вагон остановится, сжав пружину. Энергия деформированной пружины
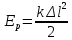 . .
По закону сохранения энергии
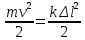
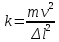
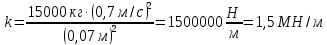
Ответ k=0,9 МН/м
|
151. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению 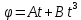 , где , где 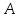 =2 рад/с, В= =2 рад/с, В=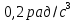 . Определить вращающийся момент М, действующий на стержень через время t = 3 с после начала вращения, если момент инерции стержня . Определить вращающийся момент М, действующий на стержень через время t = 3 с после начала вращения, если момент инерции стержня 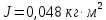 . .
Дано
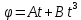
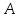 =2 рад/с =2 рад/с
В=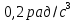
t = 3 с
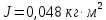
Найти:
М - ?
|
Решение
Вращающий момент по основному закону динамики для вращательного движения
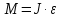
где 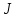 - момент инерции стрежня; - момент инерции стрежня;
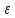 - угловое ускорение. - угловое ускорение.
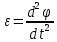
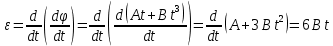
Для момента времени t = 3 с
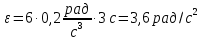
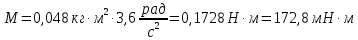
Ответ: 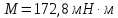
|
171. На краю неподвижной скамьи Жуковского диаметром D=0,7 м и массой m1=5 кг стоит человек массой m2=70 кг. С какой угловой скоростью ω начнет вращаться скамья, если человек поймает летящий на него мяч массой m=0,4 кг? Траектория мяча горизонтальна и проходит на расстоянии r=0,45 м от оси скамьи. Скорость мяча v=4 м/с.
Дано
D=0,7 м
m1=5 кг
m2=70 кг
m=0,4 кг
r=0,45 м
v=4 м/с
Найти
ω - ?
|
Решение
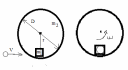
Воспользуемся законом сохранения момента импульса
До взаимодействия мяч обладал моментом импульса:
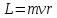
где 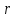 – расстояния от центра вращения до траектории полета мяча. – расстояния от центра вращения до траектории полета мяча.
Человек на платформе покоился.
После взаимодействия платформа с человеком с пойманным мячом приходит в движение, вращаясь с угловой скоростью ω. Момент импульса скамьи и человека с мячом
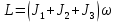 , ,
где 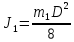 - момент инерции платформы в форме диска - момент инерции платформы в форме диска
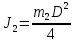 - момент инерции человека на краю платформы - момент инерции человека на краю платформы
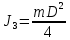 - момент инерции мяча, пойманного человеком - момент инерции мяча, пойманного человеком
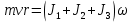
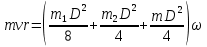
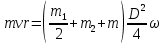
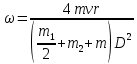
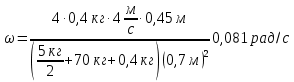
Ответ: ω =0,081 рад/с
|
181. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны 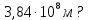
Дано
N=13
R=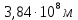
Найти:
М - ?
|
Решение
На Луну со стороны Земли действует сила, которая по закону всемирного тяготения определяется как
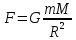 , ,
где G=6,67˔10-11 Н м2/кг2 – гравитационная постоянная
M – масса Земли
m – масса Луны
R – расстояние от Луны до Земли
По второму закону Ньютона эту силу можно выразить как
F=ma,
где 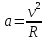 - центростремительное ускорение - центростремительное ускорение
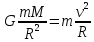
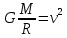
Период обращения спутника по орбите
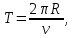
Выразим скорость
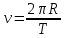
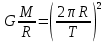
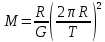
По условию Т=1 год/13 – период обращения Луны вокруг земли.
1 год=365 сут=365∙24∙3600 с
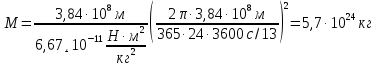
Ответ: 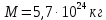
|
201. Определить концентрацию n молекул кислорода, находящегося в сосуде вместимостью V= 4 л. Количество вещества ν кислорода равно 0,5 моль
Дано
V=4 л=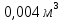
ν=0,5 моль
Найти
n - ?
|
Решение
Концентрация газа
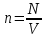 , ,
где N - число молекул
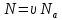
Na=6,02∙1023 моль-1 – постоянная Авогадро (число молекул в 1 моле вещества)
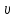 - количество вещества - количество вещества
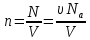
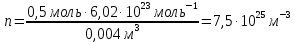
Ответ: 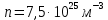
|
231. Определить показатель адиабаты γ идеального газа, который при температуре Т=350 К и давлении р=0,4 МПа занимает объем V= 300 л и имеет теплоемкость CV=857 Дж/К
Дано
р=0,4 МПа =4·105 Па
Т=350 К
V= 300 л=0,3 м3
CV=857 Дж/К
Найти
γ - ?
|
Решение
Показатель адиабаты
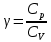 , ,
где 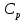 и и 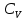 – молярные теплоемкости газа при постоянных давлении и объеме соответственно. – молярные теплоемкости газа при постоянных давлении и объеме соответственно.
Из соотношения Майера
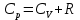 , ,
Где R= 8.31 Дж/(моль К) – газовая постоянная
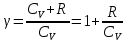
Теплоемкость газа связана с молярной теплоемкостью соотношением
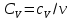
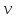 – количества вещества – количества вещества
Из уравнения Менделеева-Клайперона
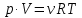
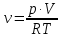
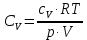
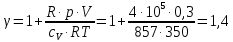
Ответ: γ=1,4
|
261. При адиабатном сжатии давление воздуха было увеличено с р1=60 кПа до р2=0,4 МПа. Затем при неизменном объеме температура была понижена до первоначальной. Определить давление р3 газа в конце процесса.
Дано
р1=60 кПа = 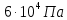
р2=0,4 МПа =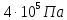
V2= V3
Т3=Т1
Найти
р3- ?
|
Решение
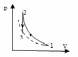
1-2 процесс адиабатный, поэтому
Q=0
Уравнение адиабатного процесса
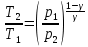
где γ- показатель адиабаты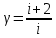 , ,
i = 5 число степеней свободы для воздуха.
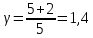
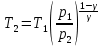
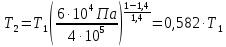
Уравнение изохорного процесса
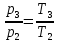
По условию 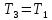
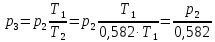
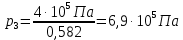
Ответ: 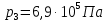
|
271. Определить работу А2 изотермического сжатия газа, совершающего цикл Карно, КПД которого η=0,38, если работа изотермического расширения равна А1=6 Дж.
Дано
η=0,38
А1= 6 Дж
Найти
А2 - ?
|
Решение
КПД тепловой машины можно найти по формуле
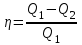 , ,
где Q1 –- количество теплоты полученной газом от теплоотдатчика, для цикла Карно в процессе изотермического расширения,
Q2 количество теплоты, отданное газом теплоприемнику, для цикла Карно в процессе изотермического сжатия.
Тогда Q2= А2 , Q1 = А1 = 6 Дж
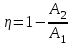
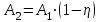
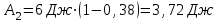
Ответ: А2 = 3,72 Дж
| |
 Скачать 86.23 Kb.
Скачать 86.23 Kb.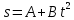 , где А=8 м, В= -2 м/с2. Определить момент времени, когда нормальное ускорение
, где А=8 м, В= -2 м/с2. Определить момент времени, когда нормальное ускорение 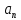 точки равно
точки равно 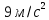 . Найти скорость
. Найти скорость 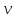 , тангенциальное
, тангенциальное 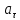 и полное
и полное 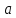 ускорение точки в тот же момент времени.
ускорение точки в тот же момент времени. 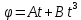 , где
, где 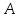 =2 рад/с, В=
=2 рад/с, В=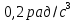 . Определить вращающийся момент М, действующий на стержень через время t = 3 с после начала вращения, если момент инерции стержня
. Определить вращающийся момент М, действующий на стержень через время t = 3 с после начала вращения, если момент инерции стержня 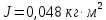 .
.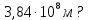

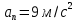
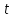 -?;
-?;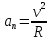
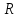 - радиус окружности.
- радиус окружности.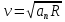
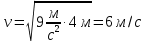
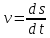
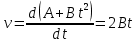
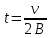
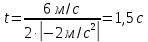
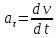
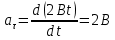
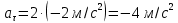
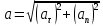
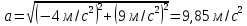
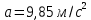 ;
; 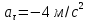 ;
; 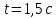 ;
; 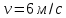
 ешение
ешение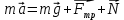 (1)
(1)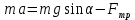 (2)
(2)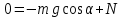 (3)
(3)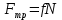 (4)
(4)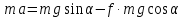
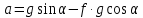
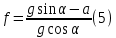
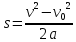
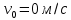
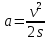
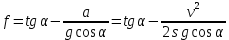
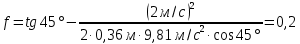
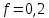
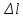 =7 см=0,07 м
=7 см=0,07 м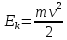
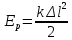 .
.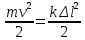
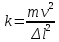
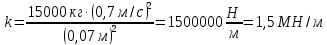
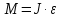
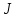 - момент инерции стрежня;
- момент инерции стрежня; 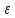 - угловое ускорение.
- угловое ускорение.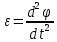
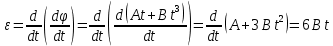
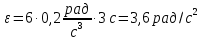
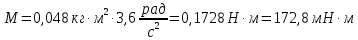
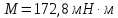

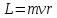
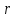 – расстояния от центра вращения до траектории полета мяча.
– расстояния от центра вращения до траектории полета мяча.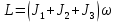 ,
,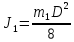 - момент инерции платформы в форме диска
- момент инерции платформы в форме диска 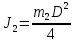 - момент инерции человека на краю платформы
- момент инерции человека на краю платформы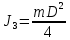 - момент инерции мяча, пойманного человеком
- момент инерции мяча, пойманного человеком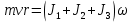
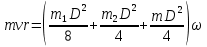
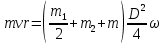
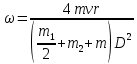
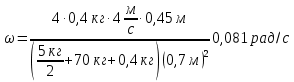
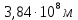
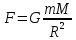 ,
, 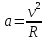 - центростремительное ускорение
- центростремительное ускорение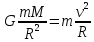
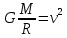
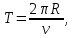
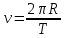
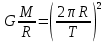
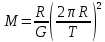
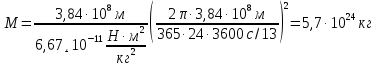
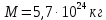
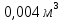
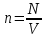 ,
,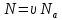
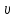 - количество вещества
- количество вещества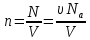
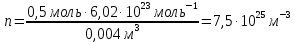
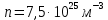
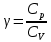 ,
,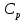 и
и 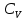 – молярные теплоемкости газа при постоянных давлении и объеме соответственно.
– молярные теплоемкости газа при постоянных давлении и объеме соответственно.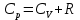 ,
,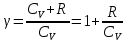
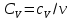
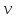 – количества вещества
– количества вещества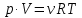
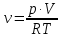
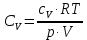
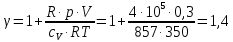
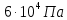
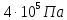

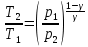
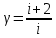 ,
, 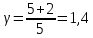
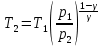
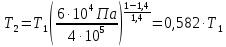
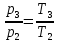
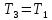
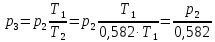
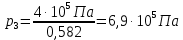
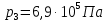
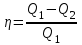 ,
,