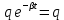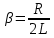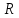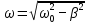учеb. Решение При решении задачи 1 мы получим уравнение смещения в виде скорость определим по формуле
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
вфвфывввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввв 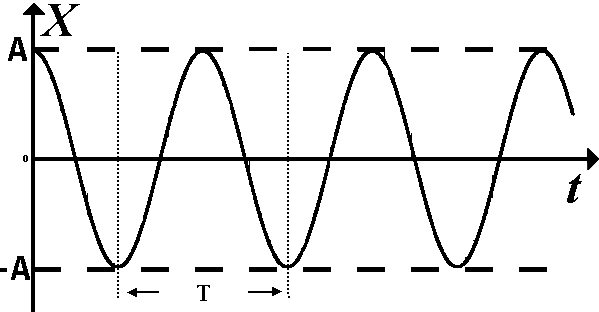 Рис.7.1.3 Добавим к условию задачи такие вопросы: определить скорость в момент времени 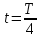 и потенциальную энергию в этот момент времени. и потенциальную энергию в этот момент времени.Решение При решении задачи 1 мы получим уравнение смещения в виде: скорость определим по формуле 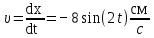 , ,Для момента времени 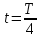 найдем фазу колебаний: найдем фазу колебаний: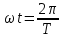 ; ; 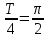 тогда скорость будет равна 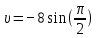 ; ; 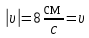 это максимальное значение скорости. На примере математического маятника (Рис.7.1.4) можно пояснить знак «минус» у скорости. 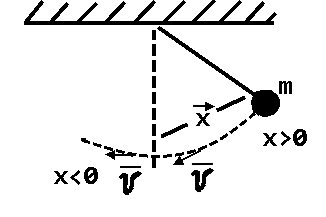 Рис.7.1.4 Потенциальная энергия определяется по формуле 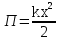 , где , где 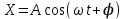 выше было получено: выше было получено: 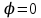 , , 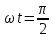 , ,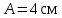 , подставим значения и получим, что потенциальная энергия равна нулю. , подставим значения и получим, что потенциальная энергия равна нулю.Это было ясно уже тогда, когда мы получили результат, что в момент времени 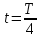 скорость приняла максимальное значение, следовательно, кинетическая энергия тоже максимальна, а потенциальная энергия равна 0. скорость приняла максимальное значение, следовательно, кинетическая энергия тоже максимальна, а потенциальная энергия равна 0.Пример 2 решения задачи 7 Дифференциальное уравнение для колебания имеет вид: 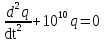 Определить частоту колебаний в Герцах Записать уравнения измерения заряда на пластинах конденсатора Записать уравнения изменения тока в контуре со временем, если в начальных момент 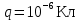 Определить индуктивность катушки, если в начальных момент максимальное напряжение на пластинах конденсатора равно 50В. Начертить графики q(t) и i(t) Решение задачи. Из вида дифференциального уравнения определяем 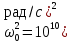 Решением дифференциального уравнения будет уравнение в виде 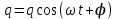 (можно записать 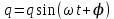 см. примечание в решении задачи 1). см. примечание в решении задачи 1).Так как в момент времени 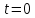 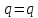 получим получим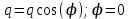 Уравнение изменения заряда на пластинах конденсатора примет вид 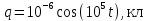 Сила тока 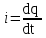 , тогда уравнение изменения силы тока со временем будет записано в виде: , тогда уравнение изменения силы тока со временем будет записано в виде: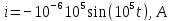 или или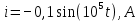 Собственная циклическая частота колебаний 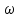 определяется параметрами контура определяется параметрами контура 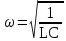 , отсюда , отсюда 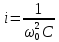 из условия задачи в момент времени из условия задачи в момент времени 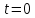 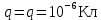 , а , а 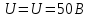 , определим емкость конденсатора , определим емкость конденсатора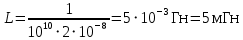 Графики зависимостей q(t) и i(t) даны на Рис.7.1.5. 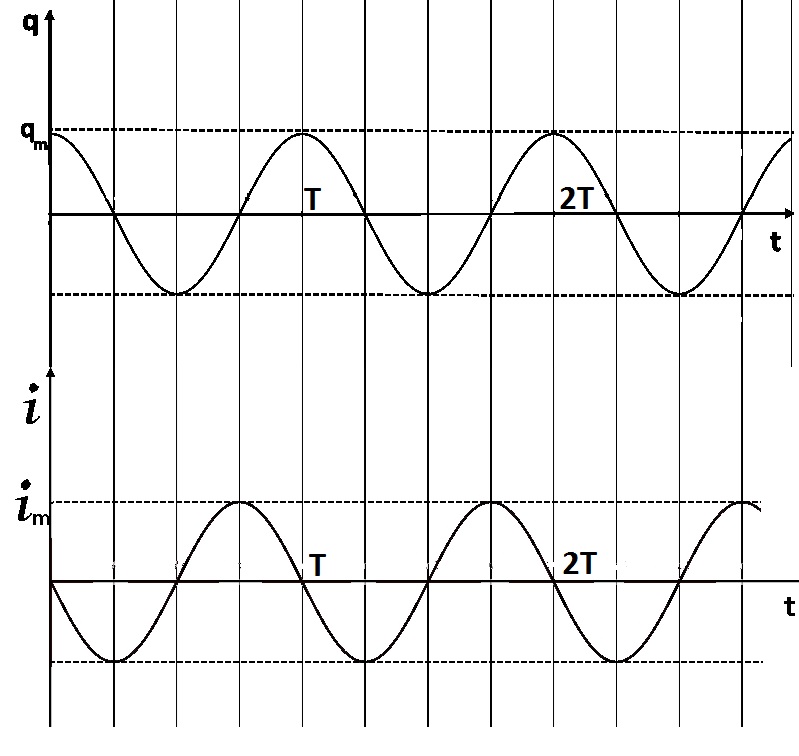 Рис.7.1.5. ЗАТУХАЮЩИЕ КОЛЕБАНИЯХ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ В любой реальной системе всегда имеются силы сопротивления, энергия системы уменьшается, т.к. частично расходуется на работу против сил трения, амплитуда колебаний со временем убывает. Затухающие колебания рассматриваем на примере колебаний в электрическом контуре. Любой реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постоянно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания в контуре затухают. Дифференциальное уравнение колебания заряда Для колебаний заряда в электрическом контуре, содержащем R, L, C, дифференциальное уравнение имеет вид: 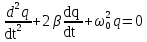 Уравнение колебания заряда Заряд на пластинах конденсатора меняется по закону 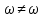 Это уравнение является решением дифференциального уравнения
Подставив значения 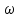 и и 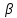 в формулу частоты колебаний ( в формулу частоты колебаний (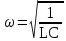 ), получим: ), получим: 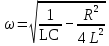 Логарифмический декремент затухания Для характеристики затухания вводится физическая величина – логарифмический декремент затухания 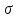 , равный натуральному логарифму отношения двух амплитуд, следующих друг за другом через период, формула определения такая: , равный натуральному логарифму отношения двух амплитуд, следующих друг за другом через период, формула определения такая: 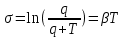 (см рис 7.2.1) (см рис 7.2.1)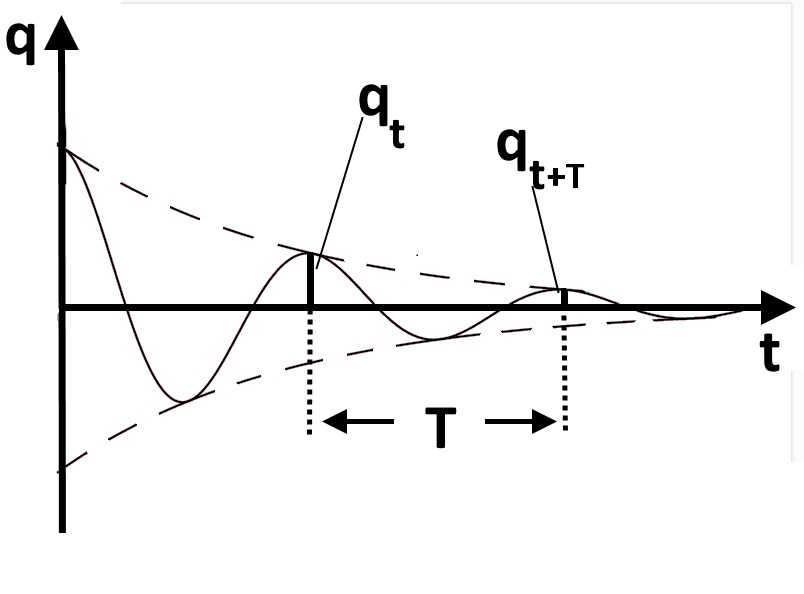 Рис.7.2.1 Время релаксации 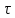 - это время, в течении которого амплитудное значение уменьшается в е раз. - это время, в течении которого амплитудное значение уменьшается в е раз.Добротность контура 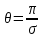 Изменение со временем разности потенциалов на пластинах конденсатора можно записать, если учесть, что 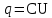 , тогда , тогда 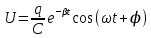 . .Обозначив 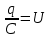 , значение разности потенциалов запишется в виде: , значение разности потенциалов запишется в виде: 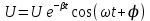 , где , где 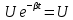 - амплитудное значение разности потенциалов. - амплитудное значение разности потенциалов.Сила тока в катушке определяется как тогда 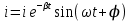 , где , где 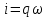 - значение тока в момент времени t=0 - значение тока в момент времени t=0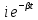 - амплитудное значение тока - амплитудное значение токаЭнергия контура будет складываться из энергии магнитного поля и энергии электрического поля 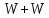 , где , где 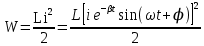 , , 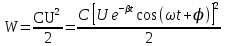 Полная энергия в любой момент времени будет равна максимальной энергии электрического поля или максимальной энергии магнитного поля: 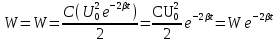 , где , где 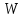 - полная энергия контура в момент времени t=0. - полная энергия контура в момент времени t=0. Приведенные ниже примеры решения задач должны вам помочь в выполнении контрольных работ. Пример 3 решения задачи № 7 Емкость электрического контура С=100пФ в начальный момент времени заряжена до максимальной величины заряда 10нКл, сопротивление 100 Ом, индуктивность 10мГн, логарифмический декремент затухания равен 0,1. Написать уравнения колебаний для: Заряда Разности потенциалов на пластинках конденсатора Записать дифференциальное уравнение для заряда Решение задачи Уравнение колебания заряда в общем виде записывается так: 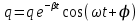 . По условию задачи в момент времени t=0 . По условию задачи в момент времени t=0 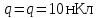 , , 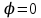 (см. свободные гармонические колебания задача 1). (см. свободные гармонические колебания задача 1).Тогда можно найти 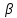 и и 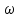 : : 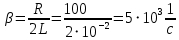 Логарифмический декремент 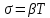 Найдем период колебаний 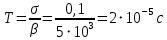 , т.к. , т.к. 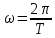 , то , то 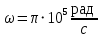 . .Уравнение колебания заряда будет иметь вид: 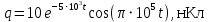 Уравнение колебания разности потенциалов в общем виде запишется так: 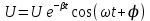 , ,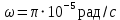 , , 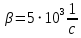 , , 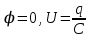 . . С – емкость конденсатора = 100 пФ 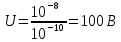 Уравнение колебания для U будет иметь вид: 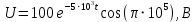 Пример 4 решения задачи № 7 Дифференциальное уравнение для заряда запишется так: 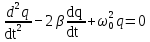 , ,Найти время, в течение которого энергия контура уменьшается в 10 раз. Решение задачи Полная энергия контура в любой момент времени определяется по формуле: 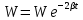 , в начальный момент времени t=0 энергия будет равна , в начальный момент времени t=0 энергия будет равна 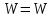 , тогда , тогда 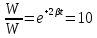 (по условию задачи). Прологарифмируем: (по условию задачи). Прологарифмируем: 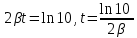 . .Из дифференциального уравнения 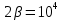 получим получим 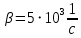 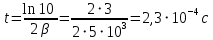 СЛОЖЕНИЕ КОЛЕБАНИЙ Возможны случаи, когда тело участвует одновременно в нескольких колебаниях, происходящих вдоль одного и того же или вдоль различных направлений. Сложение колебаний одинаково направления. Сложение колебаний с одинаковыми частотами. Допустим, что тело одновременно участвует в двух гармонических колебаниях: 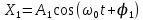 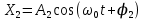  -смещение в первом из колебаний при отсутствии второго. -смещение в первом из колебаний при отсутствии второго. - смещение при втором колебании в отсутствии первого. При одновременно происходящих колебательных процессах в каждое мгновение результирующее смещение X будет равно - смещение при втором колебании в отсутствии первого. При одновременно происходящих колебательных процессах в каждое мгновение результирующее смещение X будет равно 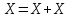 . Сложение колебаний одного направления и одинаковых частот производят по методу векторных диаграмм. Каждое колебание изображается в виде вектора, имеющего длину, равную амплитуде колебания, вращающегося вокруг начала координат с угловой скоростью, равной круговой частоте колебаний, а начальное положение вектора определяется его начальной фазой колебаний. При сложении двух колебаний с одинаковыми частотами получим результирующее колебание, которое будет являться диагональю параллелограмма. Векторы вращаются с одной и той же угловой скоростью, поэтому и результирующий вектор будет вращаться с той же угловой скоростью. Следовательно, результирующее колебание будет тоже гармоническим, смещение меняется по закону . Сложение колебаний одного направления и одинаковых частот производят по методу векторных диаграмм. Каждое колебание изображается в виде вектора, имеющего длину, равную амплитуде колебания, вращающегося вокруг начала координат с угловой скоростью, равной круговой частоте колебаний, а начальное положение вектора определяется его начальной фазой колебаний. При сложении двух колебаний с одинаковыми частотами получим результирующее колебание, которое будет являться диагональю параллелограмма. Векторы вращаются с одной и той же угловой скоростью, поэтому и результирующий вектор будет вращаться с той же угловой скоростью. Следовательно, результирующее колебание будет тоже гармоническим, смещение меняется по закону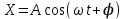 где 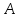 - амплитуда результирующего колебания, - амплитуда результирующего колебания,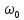 - циклическая частота колебаний, - циклическая частота колебаний,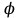 - начальная фаза результирующего колебания. - начальная фаза результирующего колебания. Рис.7.3.1 Амплитуду и фазу результирующего колебания легко найти из рассмотрения соответствующих треугольников 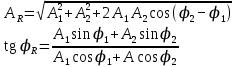 Биения В случае, когда складываемые колебания происходят по законам 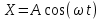 и и 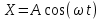 с небольшой разностью частот с небольшой разностью частот 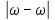 (или (или 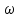 ) возникают биения. Результирующее колебание описывается уравнением ) возникают биения. Результирующее колебание описывается уравнением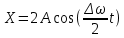 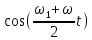 в котором выражение 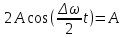 является амплитудой биений. Частота колебаний равна среднему арифметическому частот складываемых колебаний. является амплитудой биений. Частота колебаний равна среднему арифметическому частот складываемых колебаний.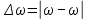 - разность частот складываемых колебаний, следовательно, при биениях амплитуда меняется по гармоническому закону с частотой биений - разность частот складываемых колебаний, следовательно, при биениях амплитуда меняется по гармоническому закону с частотой биений 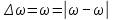 . .Период биений равен 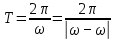 (Рис.7.3.2) (Рис.7.3.2)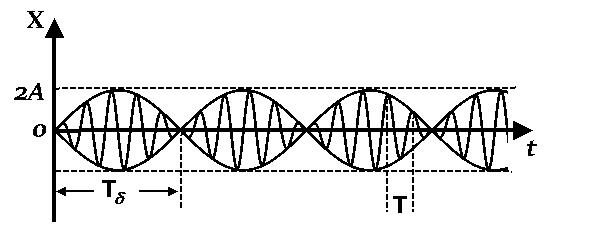 Рис.7.3.2 |