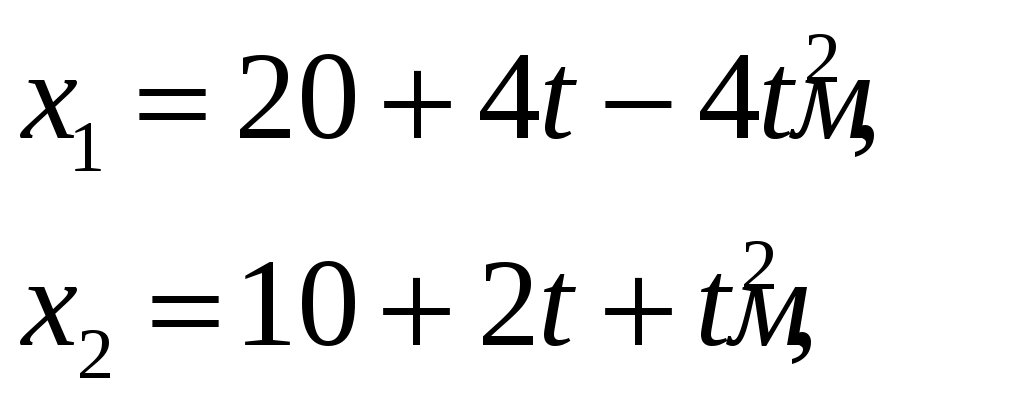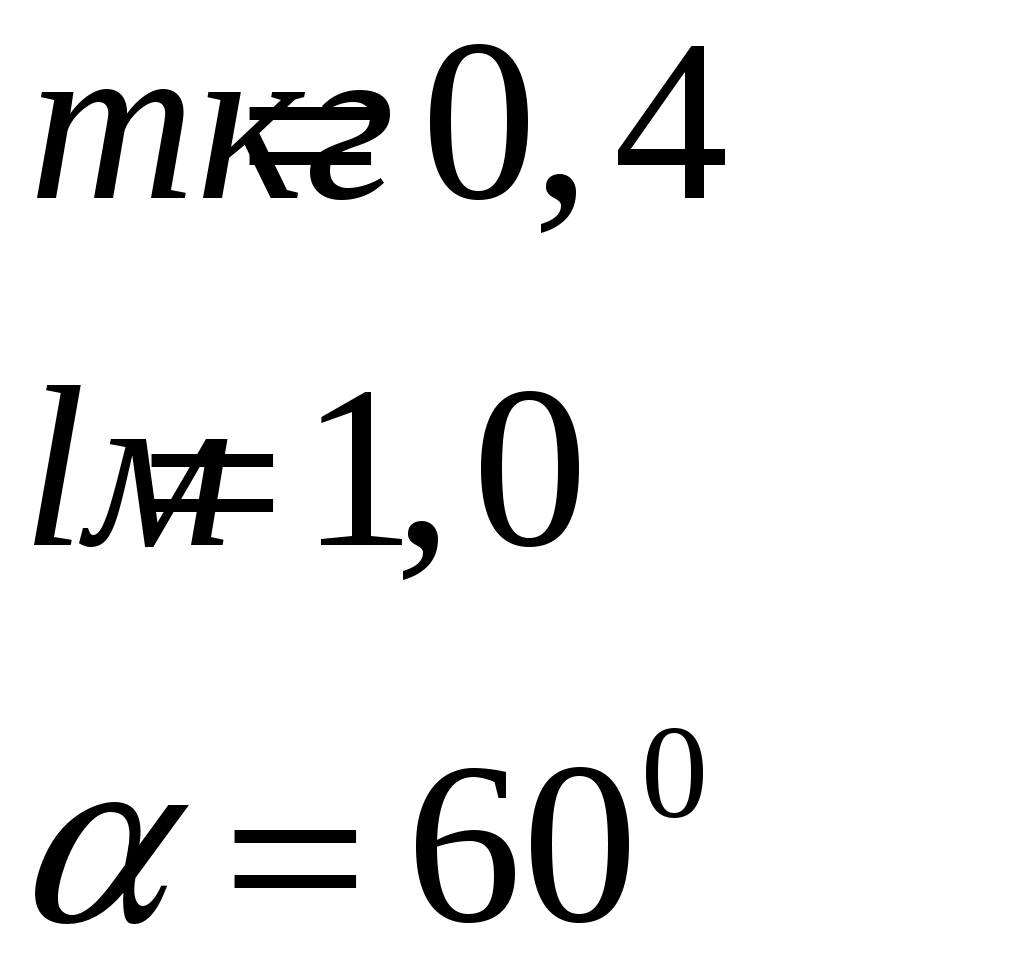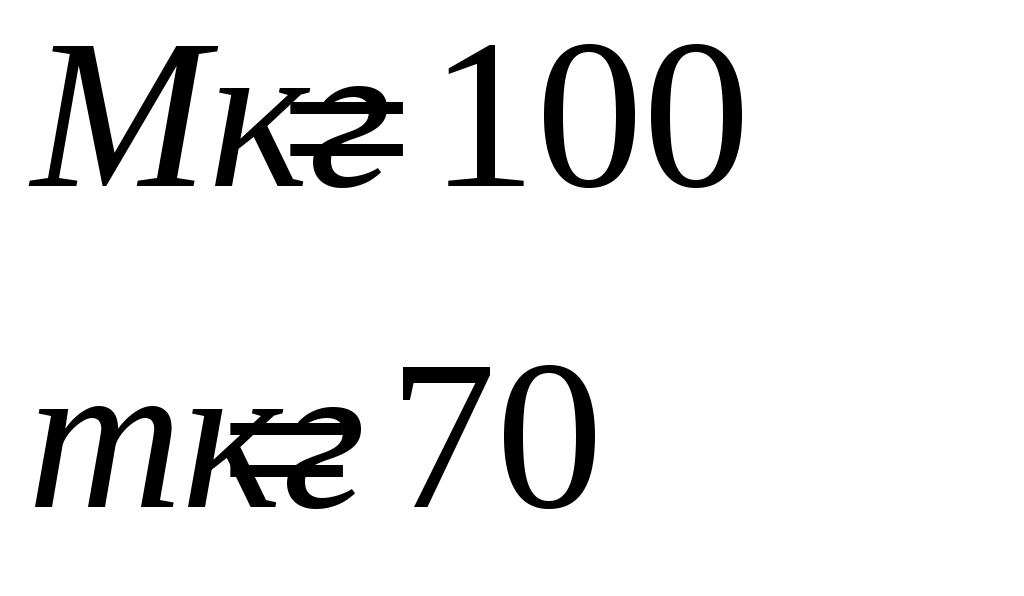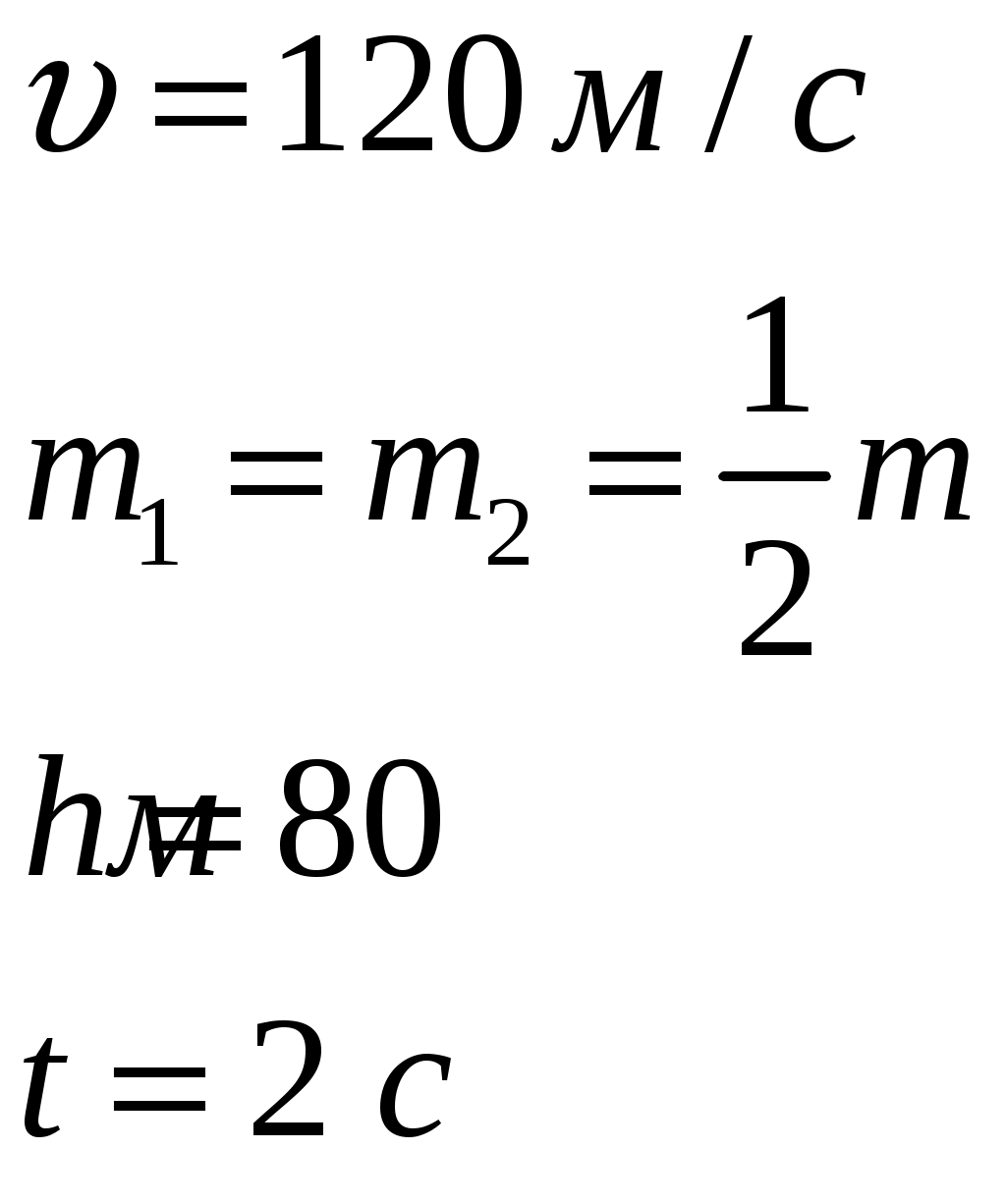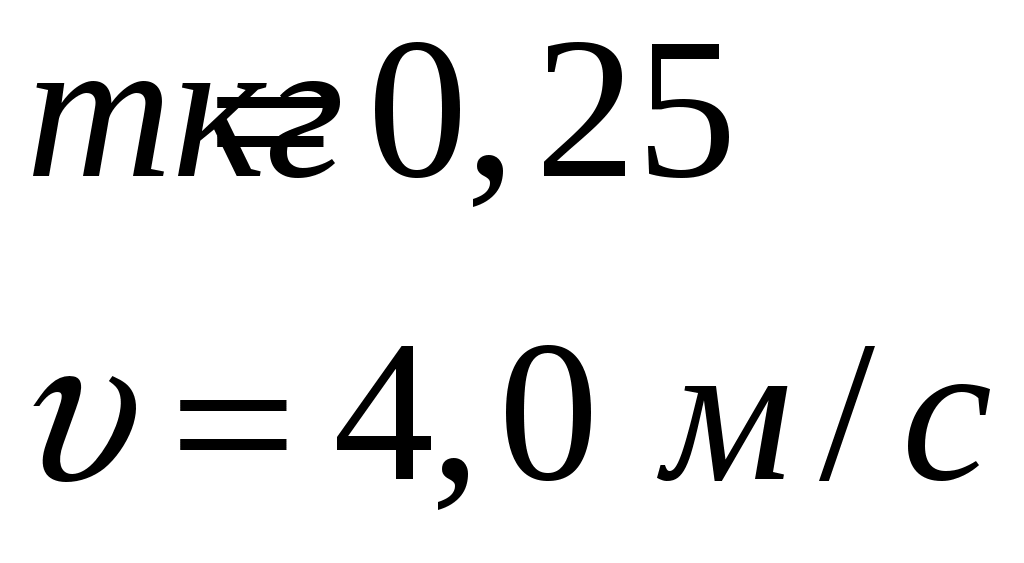Физика. Решение Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату по времени (1) (2)

• Название: Решение Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату по времени (1) (2)
• Анкор: Физика
• Дата: 10.05.2022
• Размер: 361 Kb.
• Имя файла: 1299_f_41_krfizika-1-semestr-mtusi.doc
• Тип: Решение; #520717

Физика

103. Движение двух материальных точек описываются уравнениями (в единицах СИ) и . В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения движения точек в этот момент времени.

Дано:

Найти:

Решение:

Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату по времени:

(1)

(2)

По условию задачи нужно определить момент времени, когда скорости точек одинаковы, т.е.: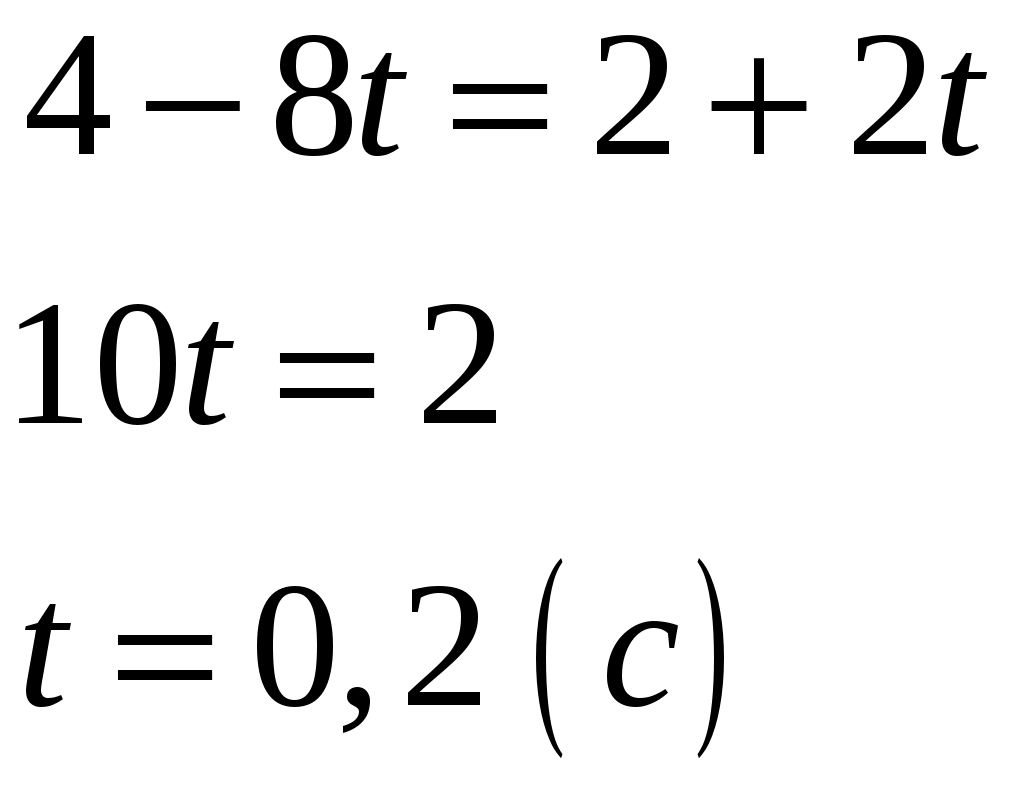





Зависимость ускорения от времени найдем, используя определение ускорения, как первой производной от скорости 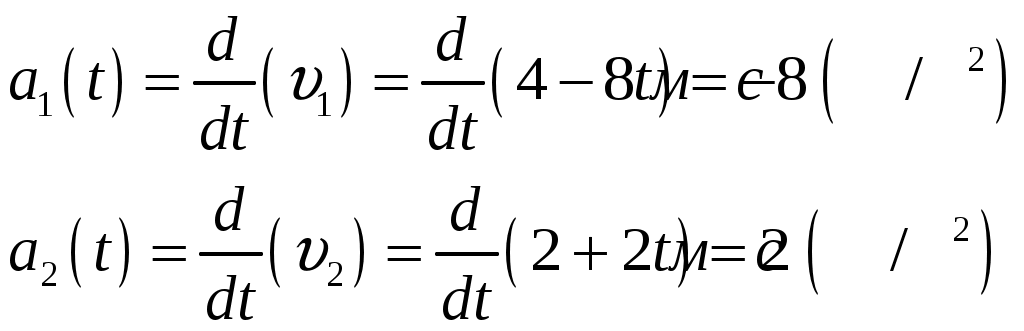по времени:



Ускорения от времени не зависят, поэтому: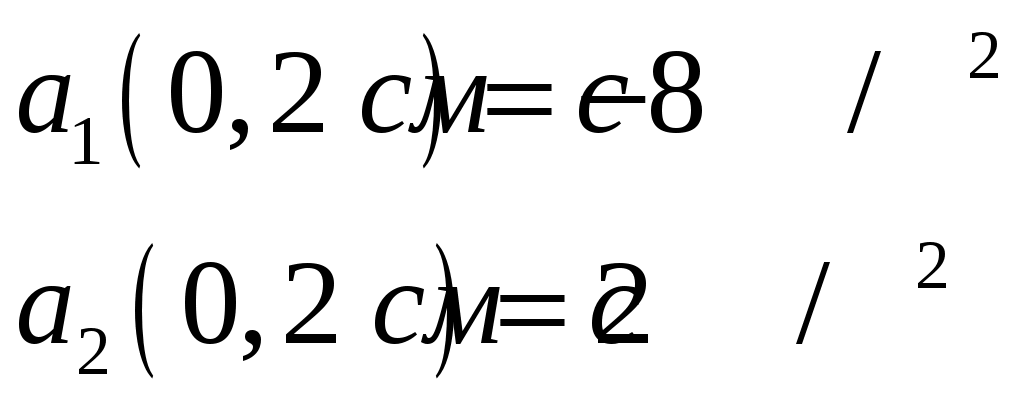



Ответ: скорости материальных точек равны при

.

113*. Шарик массой 0,4 кг, подвешенный на нити длиной 1,0 м, движется по окружности в горизонтальной плоскости так, что нить описывает конус и составляет с вертикалью угол 60°. Определить период обращения шарика и силу натяжения нити. Масса нити пренебрежимо мала.

Дано:

Найти:

Решение: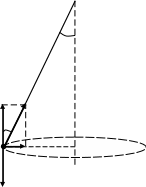






α
l

F_натcosα
α

R

F_натsinα




При движении на шарик действуют силы: сила тяжести сила натяжения нити .

Разложим силу натяжения нити на горизонтальную составляющую и вертикальную составляющую .

Запишем второй закон Ньютона в векторной форме:

(1)

где масса шарика, ускорение шарика; ускорение свободного падения.

Проведем оси координат, как показано на рисунке.

Запишем уравнение (1) в проекции на ось :

(2)

Из (1) сила натяжения нити: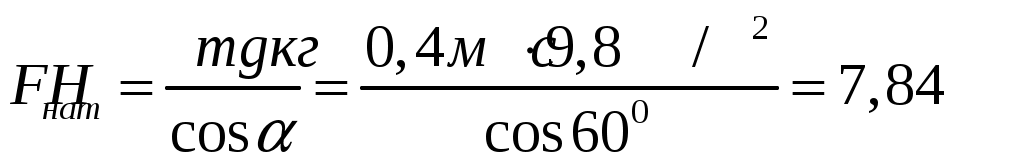

(3)

Запишем уравнение (1) в проекции на ось :

(4)

(5)

где центростремительное ускорение, угловая скорость вращения.

Радиус круга вращения из геометрии чертежа:

(6)

Из (5) находим угловую скорость, подставляя (6) и (3):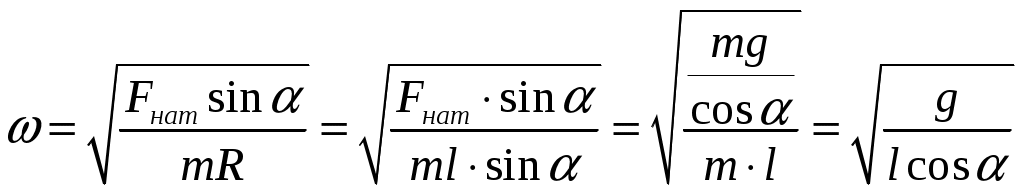

(7)

Период вращения: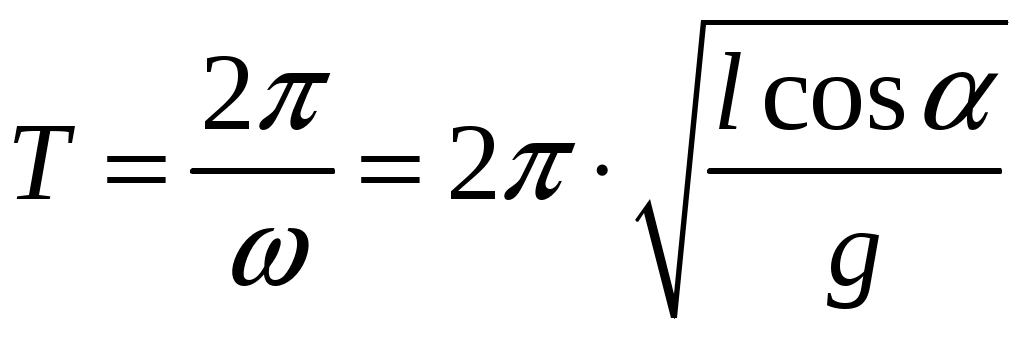

(8)

Проверим размерность формулы (8):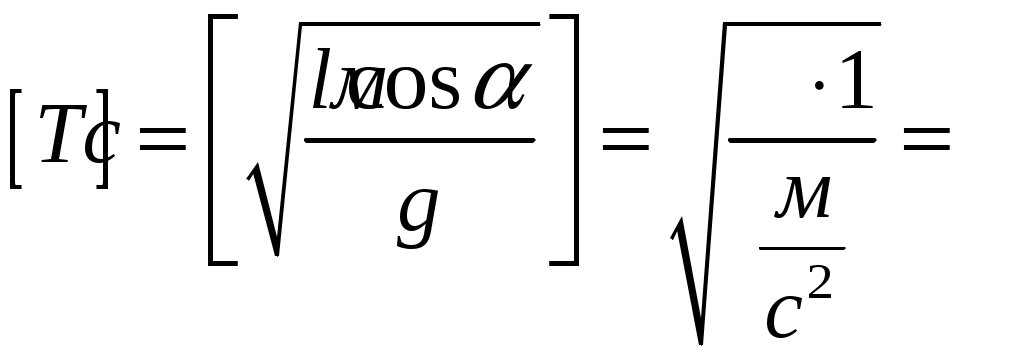



Произведем вычисления: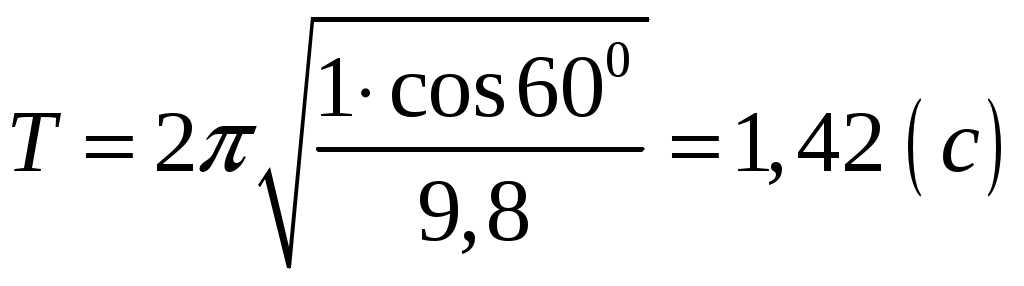

Ответ:

123.* Платформа в виде горизонтально расположенного диска может вращаться вокруг вертикальной оси, проходящей через центр платформы. На платформе находится человек, которого в условии задачи можно рассматривать как материальную точку. Расходом энергии на преодоление сил трения пренебречь. Человек массой 70 кг стоит на неподвижной платформе массой 100 кг. Человек обходит платформу вдоль ее края и останавливается в той точке платформы, от которой начал обход. На какой угол (в градусах) повернулась платформа?

Дано:

Найти:

Решение: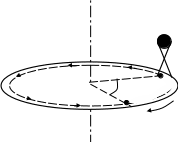












Момент инерции платформы находим как момент инерции однородного диска:

(1)

где радиус платформы; масса платформы.

Момент инерции человека относительно оси вращения платформы (момент инерции человека рассчитываем, как для материальной точки):

(2)

где масса человека.

Человек составляет вместе с платформой замкнутую механическую систему, поэтому момент импульса этой системы должен иметь постоянное значение. Следовательно, для данного случая закон сохранения момента импульса:

(3)

где угловая скорость платформы; угловая скорость человека.

Подставим (1) и (2) в (3):

(4)

(5)

Поскольку человек вернулся в ту же точку, то угол поворота составляет 180° или

(6)

где время движения.

Из (6) находим:

(7)

Подставим (7) в (5):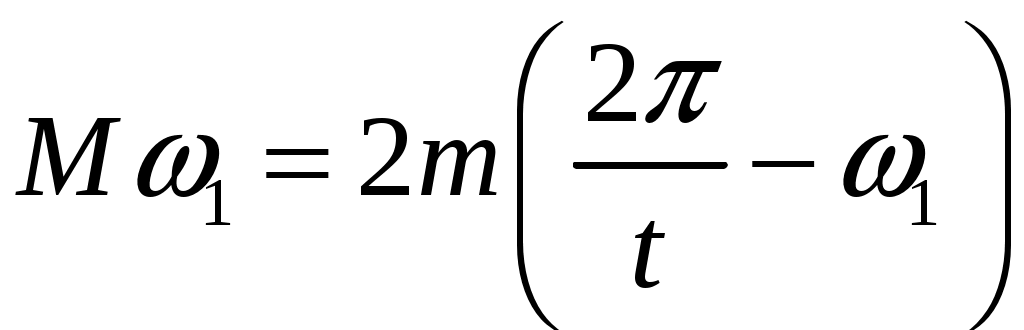

(8)

(9)

Из (8) находим: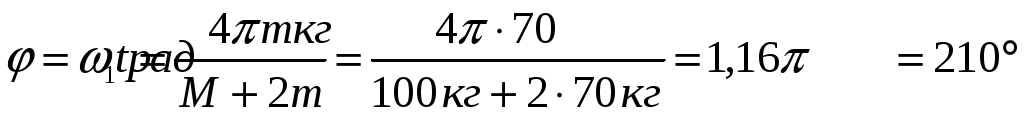



Ответ:

133.* Снаряд, летящий горизонтально со скоростью 120 м/с, разрывается на равные части на высоте 80 м. Одна часть падает через 2 секунды на землю точно под местом взрыва. Определить величину и направление скорости второй части снаряда сразу после взрыва.

Дано:

Найти:

Решение:

до разрыва после разрыва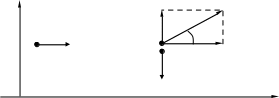




У
α






Х

Уравнение движения части 1 массой :

(1)

где высота, на которой находилась часть 1 вначале; ускорение свободного падения; время движения.

В момент удара части 1 о землю

(2)

Из (2) скорость части 1 сразу после разрыва: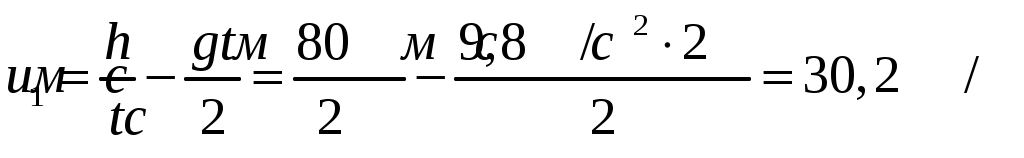



Запишем закон сохранения импульса для системы «снаряд-осколки» в векторной форме:

(3)

где импульс снаряда до разрыва; – импульс части 1 сразу после разрыва; – импульс части 2 сразу после разрыва; – скорость снаряда до разрыва.

Проведем оси координат и как показано на рисунке.

Запишем закон сохранения импульса для системы «снаряд-осколки» в проекции на ось

(4)

Запишем закон сохранения импульса для системы «снаряд-осколки» в проекции на ось :

(5)

Из (5): (6)

Запишем (4) и (6) с учетом того, что :

(7)

(8)

Разделим (8) на (7):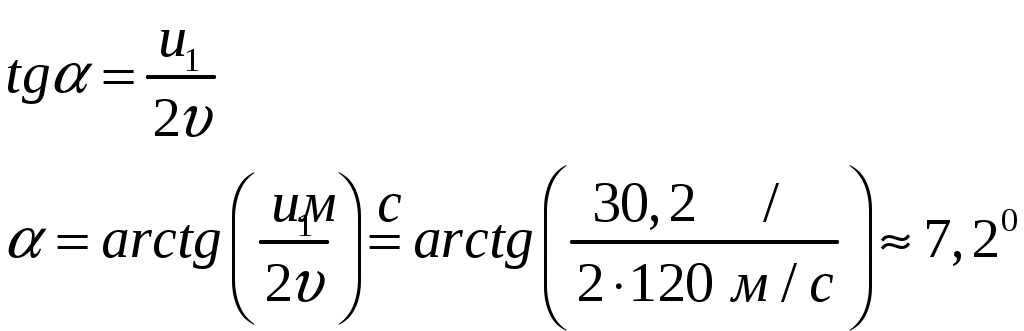





Скорость части 2 сразу после разрыва: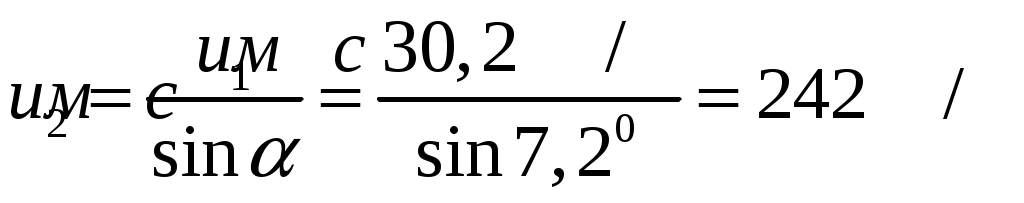



Ответ: скорость части 2 равна 242 м/с и направлена под углом 7,2° под углом к горизонту.

123. Шар массой 0,25 кг катится по горизонтальной поверхности без проскальзывания со скоростью 4,0 м/с. Определить его полную кинетическую энергию.

Дано:

Найти:

Решение:

Момент инерции шара:

(1)

где масса шара; радиус шара.

Кинетическая энергия поступательного движения шара:

(2)

Кинетическая энергия вращательного движения шара: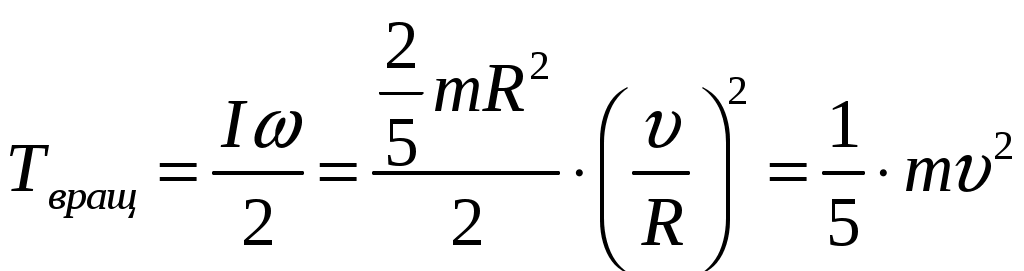

(3)

где – угловая скорость движения шара.

Полная кинетическая энергия шара складывается из кинетической энергии поступательного движения шара и кинетической энергии вращательного движения шара: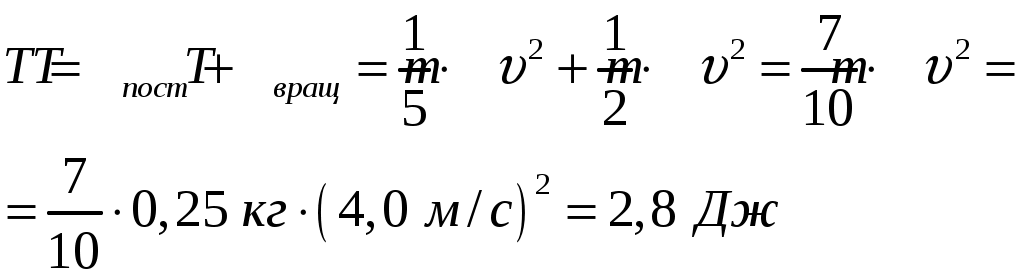



Ответ:

153. Найти скорость протона, если его полная энергия в два раза больше энергии покоя.

Дано:

Найти:

Решение:

В релятивистской механике кинетическая энергия частицы определяется как разность между полной энергией и энергией покоя этой частицы:

(1)

где масса покоя частицы; скорость света в вакууме.

Масса движущейся частицы зависит от скорости движения и связана соотношением: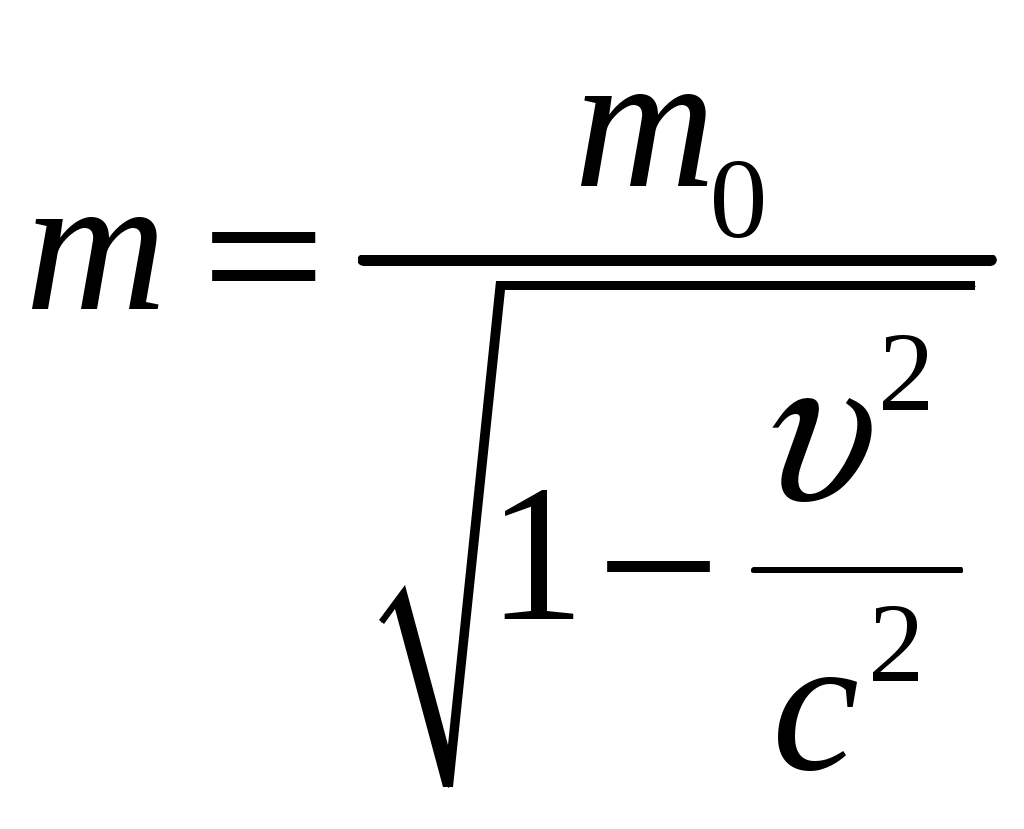

(2)

где скорость частицы

Подставим (2) в (1):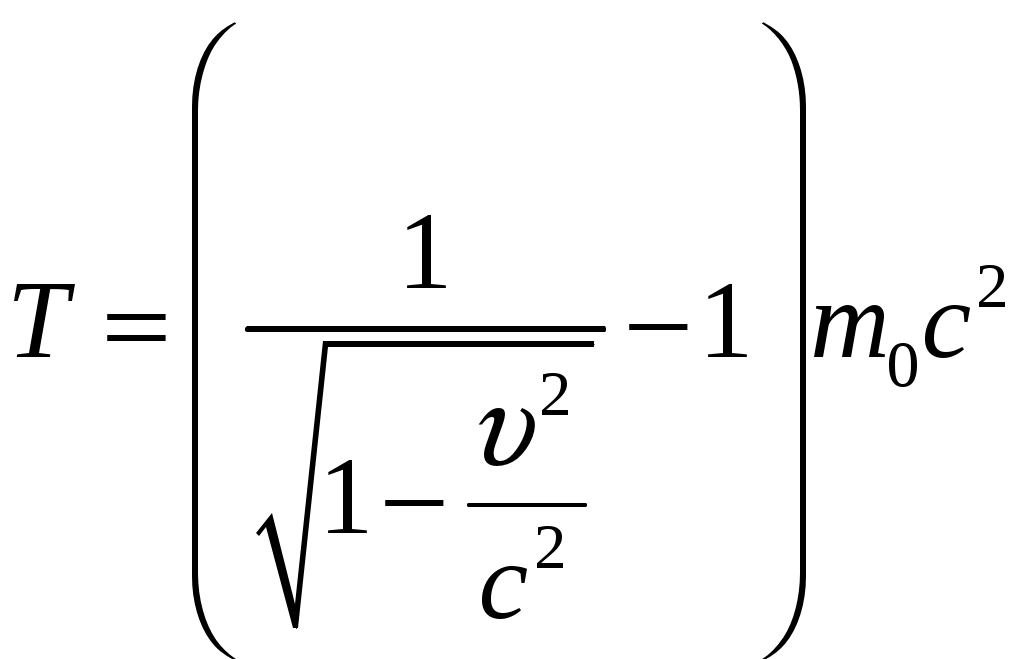

(3)

Полная энергия частицы: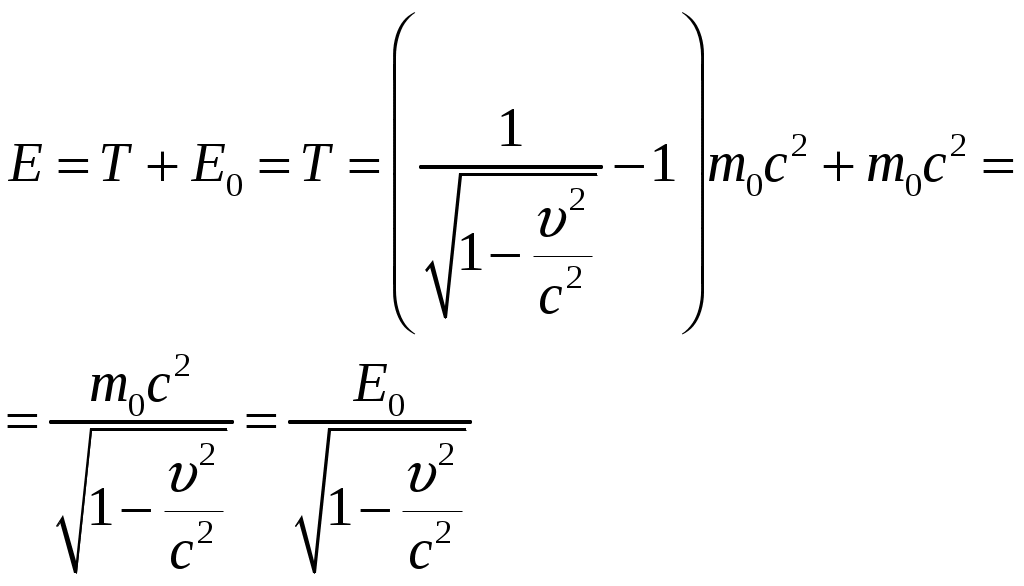

(4)

По условию задачи 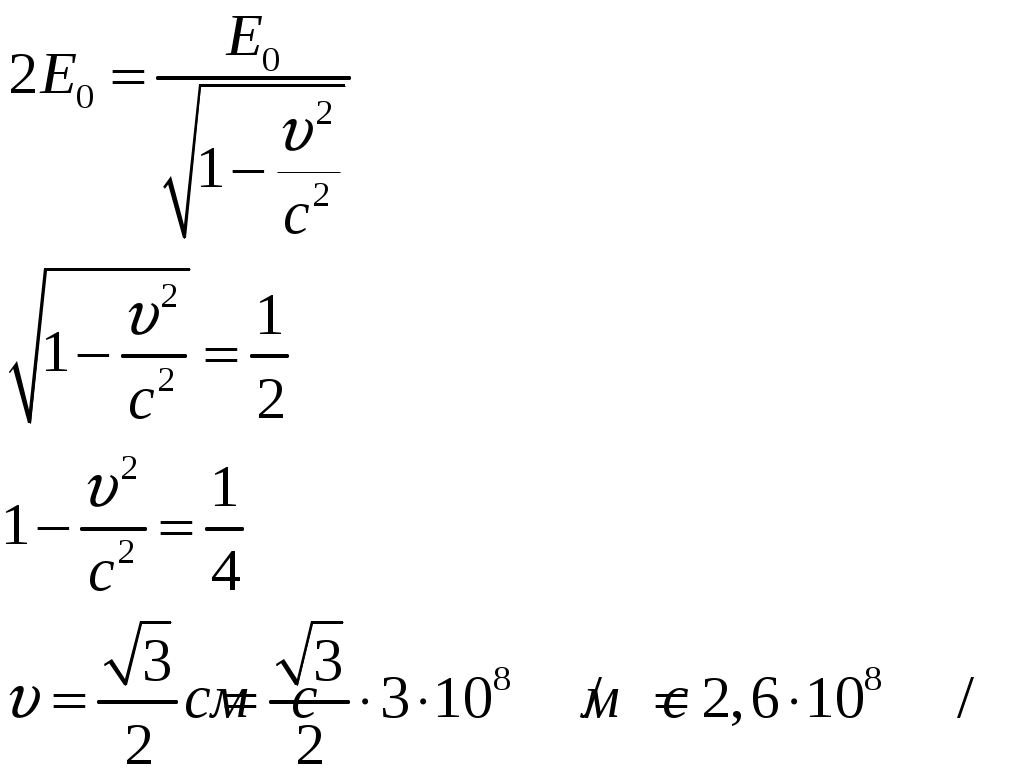, или



Ответ:

Список использованной литературы

1. 
   Детлаф А.А. Курс физики: учебник / А.А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 2002. – 718 с.
   
2. 
   Дмитриева В.Ф. Основы физики / В.Ф. Дмитриева, В.Л. Прокофьев. – М.: Высшая школа, 2003. – 527 с.
   
3. 
   Ивлиев А.Д. Физика / А.Д. Ивлев. – СПб.: Лань, 2008. – 672 с.
   
4. 
   Общая физика / коллектив авторов; под ред. А.А. Воробьёва. – М.: КНОРУС, 2016. – 800 с.
   
5. 
   Трофимова Т.И. Курс физики / Т.И. Трофимова. – М.: Издательский центр «Академия», 2006. – 560 с.