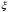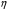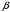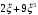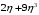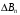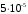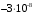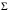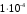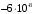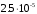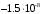Стр. механика. Епифанов. Решение задачи двухшаговым методом последовательного возмущения параметров В. В. Петрова 12 Вывод 14
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
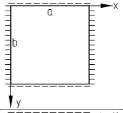
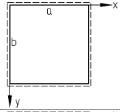
ОглавлениеЗадание №2. 1 Постановка задачи: 1 1. Построение для заданной прямоугольной пластинки статическим методом В.З. Власова аппроксимирующих функций для прогиба и функции усилий . 3 Построение эпюр 9 Опасное сечение пластинки 11 Определение максимальной грузоподъёмности пластинки 12 Решение задачи двухшаговым методом последовательного возмущения параметров В.В. Петрова 12 Вывод 14 Задание №2.Постановка задачи: В соответствии с индивидуальным заданием для прямоугольной пластинки с параметром удлиненности β необходимо: 1. Построить для заданной прямоугольной пластинки статическим методом В.З. Власова аппроксимирующие функции для прогиба 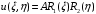 и функции усилий и функции усилий 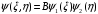 . .2. Для системы уравнений Т. Кармана составить систему вариационных уравнений метода Бубнова-Галеркина и определить величины определенных интегралов. 3. Записать систему уравнений, связывающую параметры А и В и определить эти параметры. Построить эпюры прогибов 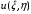 , эпюры усилий , эпюры усилий 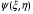 и эпюры изгибающих моментов и эпюры изгибающих моментов 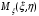 и и 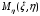 . .4. Определить опасное сечение пластинки и построить по высоте сечения эпюры 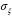 , ,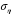 и подсчитать величину интенсивности напряжений и подсчитать величину интенсивности напряжений 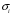 . .5. Рассчитать максимальное значение нагрузки на пластинку 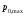 из условия из условия 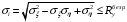 , где , где 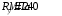 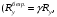 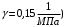 . .6. Решить задачу с использованием двухшагового метода последовательного возмущения параметров В.В. Петрова и сопоставить результат с полученным в пункте 3. 7. Провести анализ полученных результатов и сделать выводы Исходные данные: Таблица 1. Исходные данные.
1. Построение для заданной прямоугольной пластинки статическим методом В.З. Власова аппроксимирующих функций для прогиба 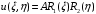 и функции усилий и функции усилий 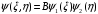 . . Построение аппроксимирующий функции для прогиба 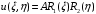 . .Рассмотрим вырезанную из пластинки вдоль оси  элементарную полоску как обыкновенную балку. элементарную полоску как обыкновенную балку.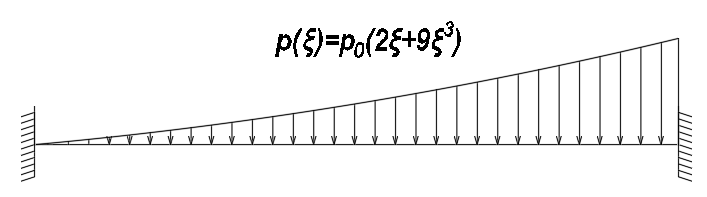 Рис.1- вырезанная балка по оси ξ Граничные условия для функции прогиба: 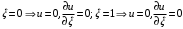 Запишем уравнение для функции прогиба в направлении оси ξ: 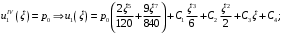 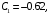 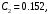 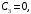 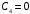 Записываем уравнение изгиба гибкой пластинки, преобразуем его к виду 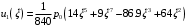 , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию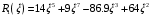 Рассмотрим вырезанную из пластинки вдоль оси 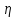 элементарную полоску как обыкновенную балку. элементарную полоску как обыкновенную балку.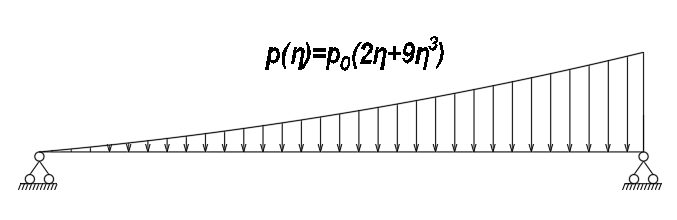 Рис.2- вырезанная балка по оси η Граничные условия для функции прогиба: 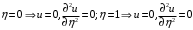 Запишем уравнение для функции прогиба в направлении оси η: 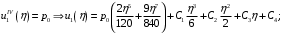 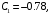 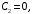 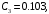 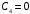 Записываем уравнение изгиба гибкой пластинки, преобразуем его к виду 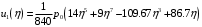 , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию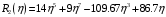 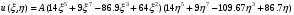 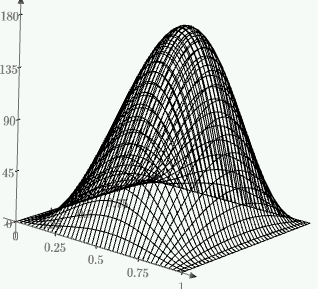 Рис.3 – функция аппроксимирующая прогиб Построение аппроксимирующий функции для функции усилий 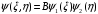 . .Рассмотрим вырезанную из пластинки вдоль оси 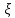 элементарную полоску как обыкновенную балку. элементарную полоску как обыкновенную балку.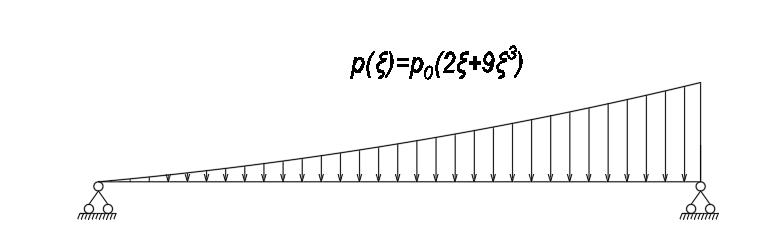 Рис.4- вырезанная балка по оси ξ Граничные условия для функции усилий: 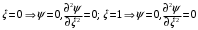 Запишем уравнение для функции усилий в направлении оси ξ: 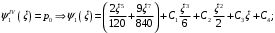 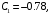 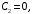 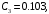 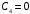 Записываем уравнение изгиба гибкой пластинки, преобразуем его к виду 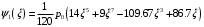 , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию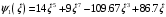 Рассмотрим вырезанную из пластинки вдоль оси 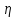 элементарную полоску как обыкновенную балку. элементарную полоску как обыкновенную балку. Рис.5- вырезанная балка по оси η Граничные условия для функции усилий: 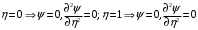 Запишем уравнение для функции усилий в направлении оси η: 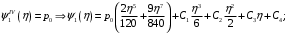 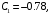 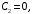 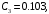 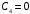 Записываем уравнение изгиба гибкой пластинки, преобразуем его к виду 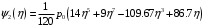 , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию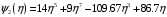 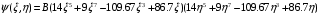 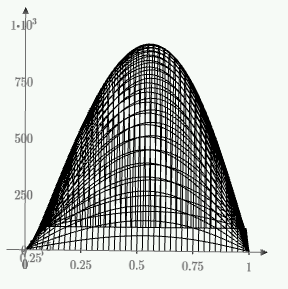 Рис.6 – функция аппроксимирующая функцию усилий Запишем систему уравнений Т. Кармана дифференциальное уравнение равновесия элемента пластинки с учетом продольной силы Nξ, а также граничных условий по оси ξ и аналитического выражения для поперечной нагрузки p(ξ). 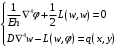 Используем следующие подстановки 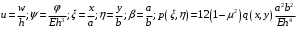 Принимаю 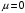 . .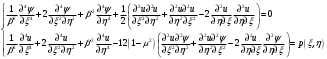 Применяем вариационное уравнению метода Бубнова-Галеркина к системе уравнений ,имеем 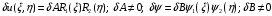 : :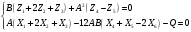 Вычислим определенные интегралы: 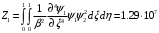 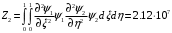 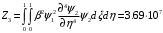 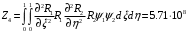 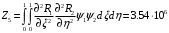 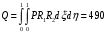 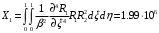 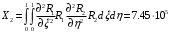 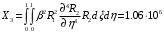 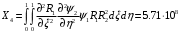 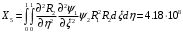 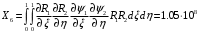 Преобразовываем и раскрываем систему 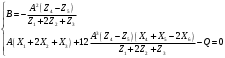 Найдем А, численная подстановка для решения кубического уравнения: 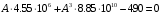 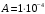 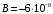 Построение эпюр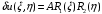 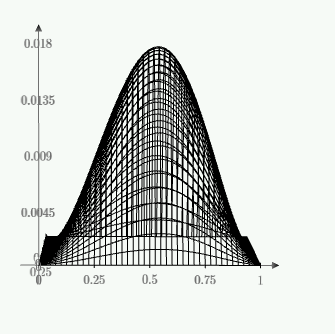 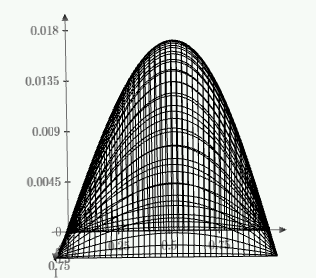 Рисунок 1 - эпюра прогиба  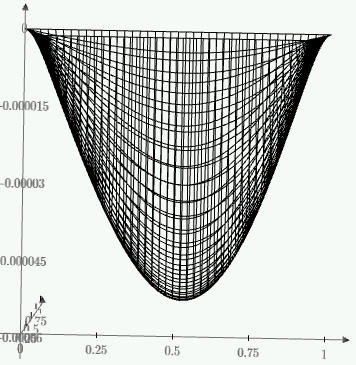 Рисунок 2 - эпюра усилий 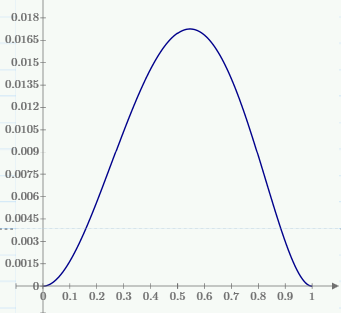 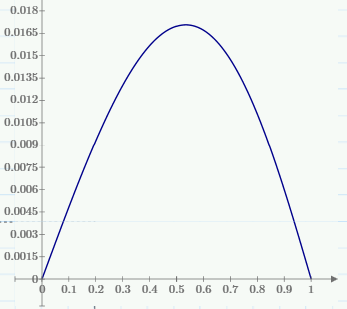 Рисунок 8 – эпюра прогиба по оси 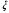 Рисунок 9 – эпюра прогиба по оси Рисунок 9 – эпюра прогиба по оси 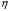 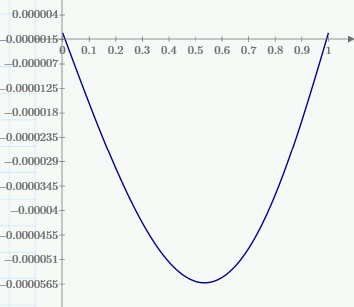 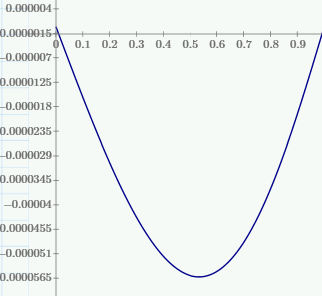 Рисунок 10 – эпюра усилий по оси 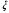 Рисунок 11 – усилий по оси Рисунок 11 – усилий по оси 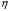 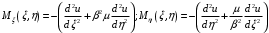 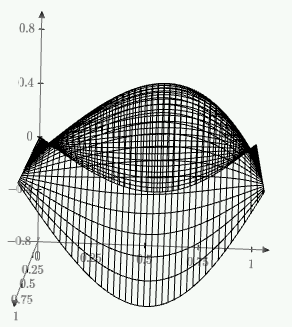 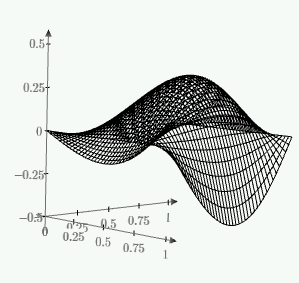 Рисунок 12 – эпюра момента по оси 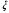 Рисунок 13 – эпюра момента по оси Рисунок 13 – эпюра момента по оси 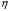 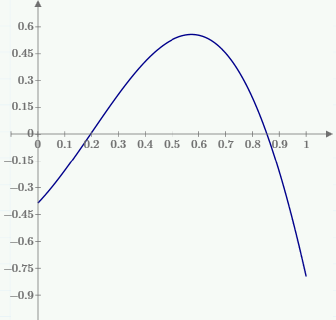 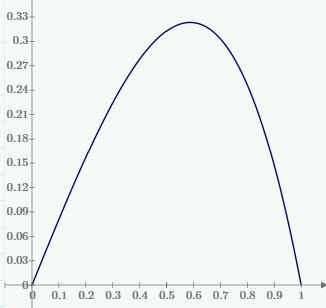 Рисунок 14 – эпюра момента по оси 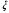 Рисунок 15 – эпюра момента по оси Рисунок 15 – эпюра момента по оси 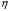 Опасное сечение пластинкиОпасное сечение пластинки проходит через точку (1;0.5;-0,5). Строим по высоте сечения эпюры нормальных напряжений вдоль осей ξ и η. 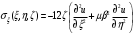  Рисунок 16 – эпюра напряжений по оси  Напряжение получаемое в результате несмещаемости опор: 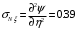 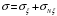  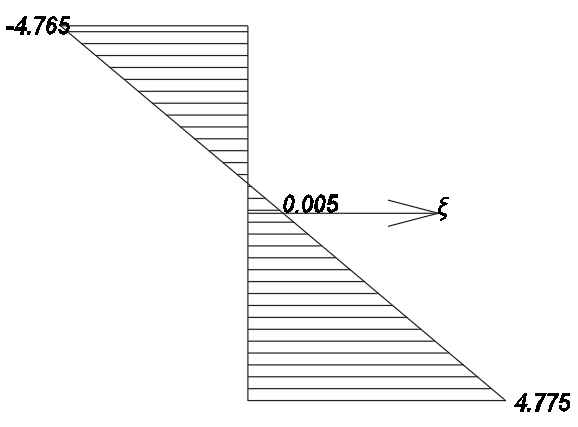 Рисунок 17 – эпюра напряжений по оси Рисунок 17 – эпюра напряжений по оси 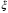 Рисунок 18 – эпюра напряжений Рисунок 18 – эпюра напряжений Определение максимальной грузоподъёмности пластинкиСогласно условию 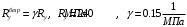 и условию прочности пластинки и условию прочности пластинки 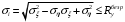 Наибольшее напряжение возникает в точке (1;0,5;0,5). Определяем значение для этой точки 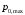 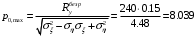 Решение задачи двухшаговым методом последовательного возмущения параметров В.В. ПетроваПреобразуя систему уравнений, а именно придаем нагрузке некоторое малое приращение 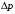 , вследствие чего прогиб получает малое приращение , вследствие чего прогиб получает малое приращение 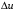 , а функция усилий получит малое приращение , а функция усилий получит малое приращение 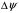 . .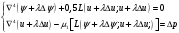 Уравнение возмущенно малым переменным параметром 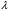 . Продифференцируем его по параметру . Продифференцируем его по параметру 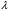 . Полагая что . Полагая что 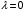 . Получаем: . Получаем: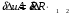 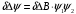 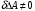 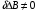 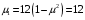 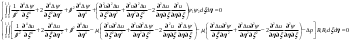 Преобразуем систему и получаем следующее выражение для определения приращения обобщенных координат ΔА иΔВ: 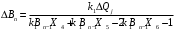 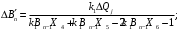 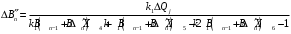 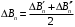 где 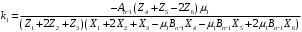 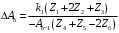 Разделяем нагрузку на 2 части j=2: 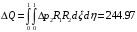 Таблица 1. Результаты расчета
Разделяем нагрузку на 4 части j=4: 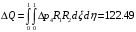 Таблица 2. Результаты расчета
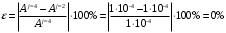 МБГ 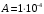 Метод Петрова Метод Петрова 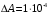 МБГ 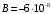 Метод Петрова Метод Петрова 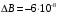 Как видно из сравнения, результаты одинаковые. ВыводДля пластинки с заданными условиями закрепления и нагрузкой построены аппроксимирующие функции прогиба и усилий статическим методом В.З. Власова. Рассчитана прямоугольная пластинка в геометрически нелинейной постановке задачи методами Бубнова-Галеркина и двухшаговым методом последовательного возмущения параметров В.В. Петрова. Результаты получились одинаковые. Результаты, приведены в виде эпюр прогиба, момента, напряжений. Полученные результаты показывают, что максимальный изгибающий момент и максимальное нормальные напряжения возникают в жестко закрепленном крае пластинки (1,0.5,-0.5) Определена максимальная грузоподъемность пластинки: 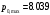 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||