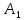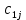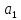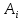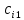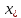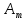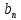Венгерский метод. Содержание введение 4 математическая постановка задачи 5 определение опорного плана 8
 Скачать 105.72 Kb. Скачать 105.72 Kb.
|
|
СОДЕРЖАНИЕ ВВЕДЕНИЕ 4 1.МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ 5 2.ОПРЕДЕЛЕНИЕ ОПОРНОГО ПЛАНА 8 2.1. Предварительные сведения 8 2.2. Метод северно-западного угла 9 2.3. Метод минимального элемента 12 3.ВЕНГЕРСКИЙ МЕТОД 16 3.1. Теоретическая справка 16 3.2. Постановка и решение задачи 18 3.3. Программная реализация задачи 24 ЗАКЛЮЧЕНИЕ 25 СПИСОК ЛИТЕРАТУРЫ 26 ПРИЛОЖЕНИЕ 1 27 ВВЕДЕНИЕЦелью настоящей курсовой работы является закрепление знаний, получаемых в процессе изучения дисциплины «Математическое моделирование», приобретение необходимых практических навыков комплексного применения теоретико-методологических принципов исследования операций и математического программирования к постановке, решению и анализу задач организационного управления. Задача данной курсовой работы состоит в следующем: изучить требуемый раздел дисциплины; построить математическую модель оптимизационной задачи, соответственно содержательной постановке; подобрать и разработать алгоритм решения поставленной задачи; написать программу, соответствующую разработанному алгоритму, отладить ее, используя в качестве тестовых данных рассчитанный вручную вариант; Тема курсовой работы – решение транспортных задач венгерским методом – является актуальной на сегодняшний день. Венгерский метод наиболее эффективен при решении транспортных задач с целочисленными объемами производства и потребления. Достоинством венгерского метода является возможность оценивать близость результата каждой из итераций к оптимальному плану перевозок. Это позволяет контролировать процесс вычислений и прекратить его при достижении определенных точностных показателей. Данное свойство существенно для задач большой размерности. Так как венгерский метод решения Т-задачи является сравнительно простым, то его можно широко применять на предприятиях, где требуется вести подсчет минимальных затрат на перевозку груза, например, со склада на предприятие. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИТранспортная задача – задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах со статичными данными и линеарном подходе. Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, специальный метод решения транспортной задачи позволяет существенно упростить ее решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок. Слово «транспортная» не означает, что такие задачи могут использоваться только для оптимизации перевозок, такое название они получили просто потому, что задачи нахождения оптимальных по критерию минимизации суммарных транспортных затрат схем прикрепления потребителей к поставщикам исторически были первыми в совокупности различных экономических проблем, решаемых с помощью моделей такого вида. Наиболее популярной является постановка математической транспортной задачи в виде:  (1.1) (1.1)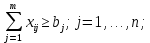 (1.2) (1.2) (1.3) (1.3) 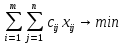 (1.4) (1.4)где 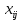 – искомые объемы перевозок продукции из пункта – искомые объемы перевозок продукции из пункта  в пункт в пункт  ; ; 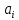 – наличие продукции в пункте – наличие продукции в пункте  (называемом обычно пунктом производства); (называемом обычно пунктом производства);  – спрос на продукцию в – спрос на продукцию в  -м пункте потребления; -м пункте потребления; 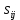 – удельные (т.е. в расчете на единицу продукции) затраты на доставку продукции из пункта – удельные (т.е. в расчете на единицу продукции) затраты на доставку продукции из пункта  в пункт в пункт  . .Постановку задачи можно найти в [1]. Если в ограничениях (1.1) правые и левые части умножить на -1, то задача (1.1) - (1.4) примет вид, соответствующий каноническому представлению математической транспортной задачи. Информация об ограничениях приводится в [2]. Поставленная задача называется закрытой транспортной задачей, если  (1.5) (1.5)в этом случае ограничения (1.1) и (1.2) выполняются как равенства на всех допустимых планах. Задача (1.1) - (1.4) называется открытой транспортной задачей, если 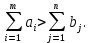 (1.6) (1.6)В этом случае многие алгоритмы решения транспортной задачи требуют ее предварительного сведения к закрытой задаче путем введения дополнительных переменных. Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие (1.5). В случае превышения запаса над потребностью (1.6) вводится фиктивный 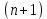 -ый пункт назначения с потребностью -ый пункт назначения с потребностью (1.7) (1.7)Соответствующие тарифы считаются равными нулю: 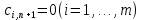 . После этих преобразований получим закрытую модель транспортной задачи. . После этих преобразований получим закрытую модель транспортной задачи.Аналогично, при  вводится фиктивный вводится фиктивный  пункт отправления с грузом пункт отправления с грузом (1.8) (1.8)а тарифы полагаются равными нулю:  . .После этих преобразований мы получим закрытую модель транспортной задачи. Обычно данные транспортной задачи записывают в виде табл. 1.1. Таблица 1.1. Представление данных транспортной задачи
Число переменных 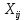 равно равно 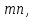 где где 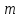 число пунктов отправления, а число пунктов отправления, а 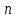 число пунктов назначения. Так как мы рассматриваем закрытую модель транспортной задачи, то число линейно независимых уравнений равно число пунктов назначения. Так как мы рассматриваем закрытую модель транспортной задачи, то число линейно независимых уравнений равно  Следовательно опорный план транспортной задачи может иметь не более Следовательно опорный план транспортной задачи может иметь не более 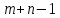 от нуля неизвестных. от нуля неизвестных.Если в опорном плане количество отличных от нуля компонентов равно в точности 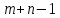 , то опорный план называется невырожденным, а если меньше – то вырожденным. , то опорный план называется невырожденным, а если меньше – то вырожденным.Для решения транспортной задачи сначала определяется начальный опорный план, а затем определяется оптимальный план путем улучшения текущего опорного плана. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||