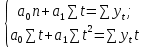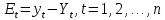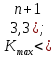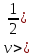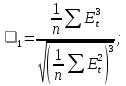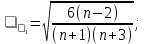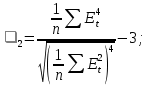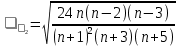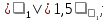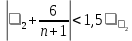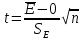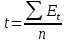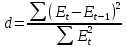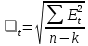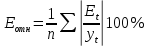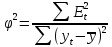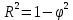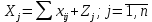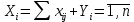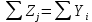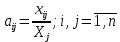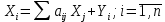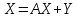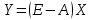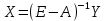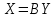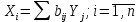Расчетно-графическая работа соц-эконом прогноз. Содержание Задания Теоретическая часть Расчетная часть Приложение а приложение б приложение в приложение г список используемой литературы Задания Задание 1
 Скачать 0.69 Mb.
|
|
Содержание Задания……………………………………………………….................3 1. Теоретическая часть…………………………………………………6 2. Расчетная часть……………………………………………………...20 3. Приложение А…………………………………………….................40 4. Приложение Б…………………………………………….................41 5. Приложение В…………………………………………….................42 6. Приложение Г…………………………………………….................44 Список используемой литературы……………………………………45 Задания Задание 1 Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год. Таблица 1
Требуется: 1) составить дискретный вариационный ряд; 2) вычислить относительные частоты (частности) и накопленные частности; 3) построить полигон; 4) найти все средние показатели; 5) найти медиану Ме и моду Мо; 6) найти дисперсию σ2 и среднее квадратическое отклонение σ. Задание 2 Из годовых отчётов производственных фирм получены следующие данные о среднегодовой стоимости основных производственных фондов (млн.руб.). Таблица 2
Необходимо произвести группировку фирм по среднегодовой стоимости производственных фондов. С целью изучения зависимости необходимо: 1) На основе равноинтервальной структурной группировки построить вариационный частотный и кумулятивный ряды распределения, оформить в таблице, изобразить графически. 2) Проанализировать вариационный ряд распределения, вычислив: среднее арифметическое, среднее гармоническое и среднее геометрическое значение признака; линейное отклонение; медиану и моду; среднее квадратичное отклонение; дисперсию; коэффициент вариации, линейный коэффициент вариации и коэффициент осцилляции. 3) Сделать выводы. Задание 3 Имеются статистические данные о затратах, связанных с рекламой по телевидению, с рекламой в метро, приведенные в таблице. Таблица 3
Создать две трендовые модели на основе кривых роста. Проверить адекватность и точность модели. Сделать прогноз на t = 4 и t = 14. Задание 4 Представлен межотраслевой баланс отчетного периода: конечная продукция отраслей (Yi) и межотраслевые потоки (Xij). Располагая данными об экономической системе, состоящей из 4 экономических объектов: Таблица 4
1. Завершить составление баланса 2. Рассчитать матрицу коэффициентов прямых затрат, полных затрат, косвенных затрат. 3. Проверить выполнение условия, гарантирующего существование решения. 4. Увеличить ассортимент конечного продукта 1-на 15%, 2-на 10%, 4-на 5%. 5. Рассчитать новую производственную программу каждого экономического объекта. 1. Теоретическая часть Вариационный ряд – ранжированный (упорядоченный) в порядке возрастания или убывания ряд статистических частот (частностей). В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды. Дискретный вариационный ряд – это ряд распределения, в котором группы составлены по признаку, изменяющемуся прерывно, т.е. через определенное число единиц и характеризуют распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Интервальный вариационный ряд – это ряд распределения, в котором группировочный признак, составляющий основание группировки, может принимать в интервале любые значения, отличающиеся друг от друга на сколь угодную малую величину. Для того, чтобы сформировать ряд и сгруппировать данные используют формулу Стерджесса:
где n – число групп; N – число единиц совокупности. Если вариация признака происходит в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами:
где xmax,xmin– максимальное и минимальное значение. Величина интервала округляется до ближайшего целого числа, или же кратного 10, 50, 100. Частотами называются численности отдельных вариант или каждой группы вариационного ряда. Частоты показывают, как часто встречаются те или иные значения признака в изучаемой совокупности. Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
где fотн – относительная частота; f – частота; n – число случаев. Накопленные частоты определяются путем последовательного прибавления к частотам (или частностям) первой группы этих показателей последующих групп ряда распределения. Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении оси абсцисс (x) и оси ординат (y) точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот. Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности. Сущность средней состоит в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. 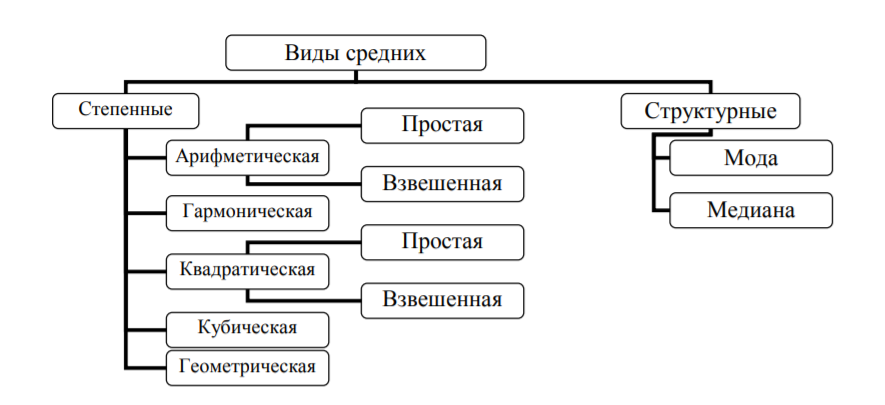 Рис. 1 Простые средние:
Взвешенные средние:
где 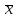 – средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений; xi – варианты (значение) осредняемого признака или серединное значение интервала, в котором измеряется вариант; n – число вариант; f – частота (повторяемость индивидуальных значений признака).Медиана (Ме) – величина, которая находится в середине вариационного ряда. Она делит ряд на две равные части. В ранжированных рядах не сгруппированных данных нахождение медианы сводится к отысканию порядкового номера и значения варианта у этого номера. Численное значение медианы определяют по формуле:
где xMe – нижняя граница медианного интервала (накопленная частота которого превышает половину общей суммы частот); hMe – величина медианного интервала; SMe-1 – накопленная частота интервала, предшествующего медианному; fMe – частота медианного интервала. Модой (Мо) называется вариант, которому соответствует наибольшая частота. Для вычисления моды в интервальном ряду сначала находится модульный интервал, имеющий наибольшую частоту, а затем вычисляется по формуле
Где xMo– нижняя границ модального интервала; hMo- величина модального интервала; fMo - частота модального интервала; fMo-1- частота интервала, предшествующего модальному; fMo+1 - частота интервала, следующая за модальным. К абсолютным показателям вариации относят размах вариации, среднее линейное отклонение, дисперсию, средне квадратическое отклонение. Размах вариации – показатель, определяющий насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака:
Среднее линейное отклонение – величина, определяющаяся как средняя арифметическая из абсолютных значений отклонений от средней. Формула среднего линейного отклонения (простая):
Формула среднего линейного отклонения (взвешенная):
Дисперсия – средняя величина квадратов отклонений индивидуальных значений признака от их средней величины. Формула дисперсии (простая):
Формула дисперсии (взвешенная):
Среднее квадратическое отклонение – корень квадратный из дисперсии. Средняя квадратическая простая:
Средняя квадратическая взвешенная:
Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации, выраженные в относительных величинах. Коэффициент осцилляции:
Линейный коэффициент вариации:
Коэффициент вариации:
Прогнозирование – это предсказание будущего на основании накопленного опыта и текущих предположений относительно него. Использование метода экстраполяции на основе кривых роста для прогнозирования базируется на двух предположениях: - временной ряд экономического показателя действительно имеет тренд, т.е. преобладающую тенденцию; - общие условия, определявшие развитие показателя в прошлом, останутся без существенных изменений в течение периода упреждения. Наиболее часто в экономике используются полиномиальные, экспоненциальные и S-образные кривые роста. Простейшие полиномиальные кривые роста имеют вид:
Параметр a1называют линейным приростом, a2- ускорением роста, параметр a3– изменением ускорения роста. На практике при предварительном выборе отбирают обычно две-три кривые роста для дальнейшего исследования и построения трендовой модели данного временного ряда. Параметры полиномиальных кривых оцениваются, как правило, методом наименьших квадратов, суть которого заключается в том, чтобы сумма квадратов отклонений фактических уровней ряда от соответствующих выровненных по кривой роста значений была наименьшей. Этот метод приводит к системе так называемых нормальных уравнений для определения неизвестных параметров отобранных кривых. Для полинома первой степени система нормальных уравнений имеет вид:
где знак суммирования распространяется на все моменты наблюдения исходного временного ряда. Системы для полинома второй и третьей системы имеют аналогичный вид. Оценка адекватности модели: Проверка случайности колебаний уровней остаточной последовательности. Для исследования случайности отклонений от тренда мы располагаем набором разностей:
Характер этих отклонений изучается с помощью ряда непараметрических критериев. Одним из таких критериев является критерий серий, основанный на медиане выборки. Ряд из величин Et располагают в порядке возрастания их значений и находят медиану Em полученного вариационного ряда. Возвращаясь к исходной последовательности Et и сравнивая значения этой последовательности с Em, будем ставить знак «плюс», если значение Etпревосходит медиану, и знак «минус», если оно меньше медианы; в случае равенства сравниваемых величин соответствующее значение Etопускается. Последовательность подряд идущих плюсов или минусов называется серией. Обозначим протяженность самой длинной серии через Kmax, а общее число серий – через v. Выборка признается случайной, если выполняются следующие неравенства для 5%-го уровня значимости:
где квадратные скобки означают целую часть числа. Если хотя бы одно из этих неравенств нарушается, то гипотеза о случайном характере отклонений уровней временного ряда от тренда отвергается и, следовательно, трендовая модель признается неадекватной. Проверка соответствия распределения случайной компоненты нормальному закону распределения Проверка соответствия распределения случайной компоненты нормальному закону распределения может быть произведена лишь приближенно с помощью исследования показателей асимметрии (i) и эксцесса (2). Мы предполагаем, что отклонения от тренда представляют собой выборку из генеральной совокупности, поэтому можно определить только выборочные характеристики асимметрии и эксцесса и их ошибки:
В этих формулах 1 — выборочная характеристика асимметрии; 2 — выборочная характеристика эксцесса; 1 и 2— соответствующие среднеквадратические ошибки. Если одновременно выполняются следующие неравенства:
то гипотеза о нормальном характере распределения случайной компоненты принимается. Проверка равенства математического ожидания случайной компоненты нулю Eсли она распределена по нормальному закону, осуществляется на основе t-критерия Стьюдента. Расчетное значение этого критерия задается формулой
где 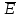 – среднее арифметическое значение уровней остаточной последовательности Et; SE – стандартное (среднеквадратическое) отклонение для этой последовательности.Если расчетное значение tменьше табличного значения t статистики Стьюдента с заданным уровнем значимости и числом степеней свободы n-1, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается; в противном случае эта гипотеза отвергается и модель считается неадекватной. Можно воспользоваться также формулой:
для вычисления математического ожидания. Проверка независимости значений уровней случайной компоненты Проверка отсутствия существенной автокорреляции в остаточной последовательности, может осуществляться по ряду критериев, наиболее распространенным из которых является d-критерий Дарбина—Уотсона. Расчетное значение этого критерия определяется по формуле:
Заметим, что расчетное значение критерия Дарбина-Уотсона в интервале от 2 до 4 свидетельствует об отрицательной связи; в этом случае его надо преобразовать по формуле d' = 4 – d и в дальнейшем использовать значение d'. Расчетное значение критерия d (или d') сравнивается с верхним d1 и нижним d2критическими значениями статистики Дарбина-Уотсона. Если расчетное значение критерия d больше верхнего табличного значения d1, то гипотеза о независимости уровней остаточной последовательности, т.е. об отсутствии в ней автокорреляции, принимается. Если значение d меньше нижнего табличного значения d2, то эта гипотеза отвергается и модель неадекватна. Если значение d находится между значениями d1 и d2, включая сами эти значения, то считается, что нет достаточных оснований сделать тот или иной вывод и необходимы дальнейшие исследования, например, по большему числу наблюдений. Вывод об адекватности трендовой модели делается, если все указанные выше четыре проверки свойств остаточной последовательности дают положительный результат. Оценка точности модели: 1. Среднеквадратическое отклонение:
где k – число определяемых параметров. 2. Средняя относительная ошибка аппроксимации:
3. Коэффициент сходимости:
где n– количество уровней 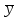ряда;  – среднеарифметическое значение уровней ряда.4. Коэффициент детерминации:
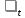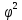Условия точности моделей:  и Eотн должны быть минимальными;  и R2должны стремиться соответственно к 0 и 1.На основании указанных показателей можно сделать выбор из нескольких адекватных трендовых моделей экономической динамики наиболее точной, хотя может встретиться случай, когда по некоторому показателю более точна одна модель, а по-другому – другая. Принципиальная схема межотраслевого баланса. Выделяются четыре части, имеющие различное социально-экономическое содержание. Они называются квадрантами баланса. I квадрант – таблица межотраслевых материальных затрат. Показатели, помещенные на пересечении строк и столбцов, представляют собой величины межотраслевых потоков продукции и в общем виде обозначаются xij. Таким образом, I квадрант представляет собой квадратную матрицу порядка n, сумма всех элементов которой равняется годовому фонду возмещения затрат средств производства. Во II квадранте представлена конечная продукция всех отраслей Yi, при этом под конечной понимается продукция, выходящая из сферы производства в область конечного использования (на потребление и накопление). II квадрант характеризует отраслевую материальную структуру национального дохода, в развернутом виде – распределение национального дохода на фонд накопления и фонд потребления. Структура потребления и накопления по отраслям производства и потребителя. III квадрант также характеризует национальный доход, но со стороны его стоимостного состава. В состав условно чистой продукции Zj входят амортизационные отчисления Cj, оплата труда vj и чистый доход отраслей mj. IV квадрант баланса отражает конечное распределение и использование национального дохода. В результате перераспределения первоначально созданного национального дохода образуются конечные доходы населения, предприятия и государства. Данные IV квадранта важны для отражения в межотраслевой модели баланса доходов и расходов населения, источников финансирования капиталовложений, текущих затрат непроизводственной сферы и для анализа общей структуры конечных доходов по группам потребителей. Итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли:
Валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:
Балансовый характер таблицы выражается в том, что ∑Xi=∑Xj Значит,
Основу информационного обеспечения МОБ составляет технологическая матрица A=(aij), содержащая коэффициенты прямых материальных затрат на производство единицы продукции. Эта матрица является основой экономико-математической модели МОБ. Величина называется коэффициентом прямых материальных затрат и рассчитывается по формуле:
Уравнение (32) можно записать:
или в матричном виде:
Система уравнений (35) или в матричной форме (36) называется экономико-математической моделью межотраслевого баланса, моделью Леонтьева. С помощью ее можно выполнить три варианта расчета: 1. Задав в модели величины валовой продукции каждой отрасли (Xi), можно определить объемы конечной продукции каждой отрасли (Yi):
2. Задав величины конечной продукции всех отраслей (Yi), можно определить величины валовой продукции каждой отрасли (Xi):
3. Для ряда отраслей задав величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. Обозначим эту обратную матрицу через В = (Е - А)-1, тогда систему уравнений в матричной форме (38) можно записать в виде
Элементы матрицы В будем обозначать через bij, тогда из матричного уравнения (39) для любой i-й отрасли можно получить следующее соотношение:
Для того чтобы матрица коэффициентов прямых материальных затрат А была продуктивной, необходимо и достаточно чтобы выполнялось одно из перечисленных ниже условий: 1) матрица (Е -А) неотрицательно обратима, т.е. существует обратная матрица (Е - A)-1>0; 2) матричный ряд Е + А + А2 + А3 + ... = сходится, причем его сумма равна обратной матрице (Е - А)-1; 3) наибольшее по модулю собственное значение матрицы А, то есть решение характеристического уравнения: 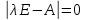 строго меньше единицы; 4) все главные миноры матрицы (Е - А), т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы, порядка от 1 до п, положительны. |
– 
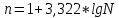
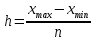
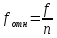
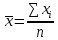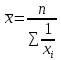– средняя гармоническая
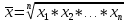- средняя геометрическая
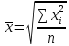– средняя квадратическая 
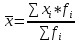– средняя арифметическая 
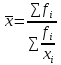– средняя гармоническая
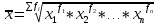– средняя геометрическая
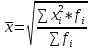– средняя квадратическая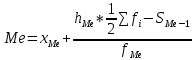
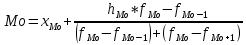
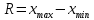
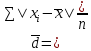
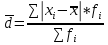
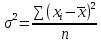
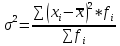
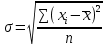
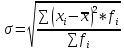
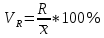
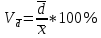
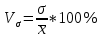
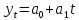(полином первой степени)
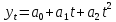(полином второй степени)
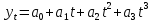(полином третьей степени)
