доклад Новиков А.Л. Теоретическая механика
 Скачать 121.9 Kb. Скачать 121.9 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВО «УДМУРТСКИЙ ГОСУДАРСТВКЕННЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ НЕФТИ И ГАЗА им. М.С. ГУЦЕРИЕВА кафедра «разработка и эксплуатация нефтяных и газовых месторождений» направление 21.03.01 – НЕфтегазовое дело «БУРЕНИЕ НЕФТЯНЫХ И ГАЗОВЫХ СКВАЖИН» РЕФЕРАТ по дисциплине «Теоретическая механика» Выполнил: студент 2 курса группы ЗУсC-21.05.06.01-22 Новиков А.Л. Проверил: к.н. доцент Борисова Е. М. ИЖЕВСК 2021 Условия равновесия системы сил в теоретической механике Содержание: Условия равновесия системы сил в векторной форме 2. Условия равновесия пространственной системы сил в аналитической форме 3. Условия равновесия пространственной системы параллельных сил 4. Условия равновесия плоской системы сил Условия равновесия системы силУсловия равновесия системы сил в векторной форме Из теоремы о приведении системы сил к силе и паре сил можно вывести условия равновесия системы сил, действующих на твердое тело. Очевидно, что если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из силы и пары сил. Чтобы такая система сил была эквивалентна _ нулю, необходимо и достаточно равенства нулю как силы Условия (11) являются векторными условиями равновесия для любой системы сил. Условия равновесия пространственной системы сил в аналитической формеЕсли при равновесии системы сил, приложенных к твердому телу, главный вектор 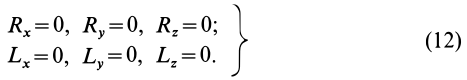 Учитывая формулы (5) и (7), эти шесть условий через силы системы выражают в форме 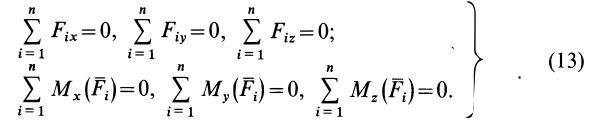 Таким образом, для равновесия пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю. Из общих условий равновесия для произвольной пространственной системы сил получаются условия равновесия для частных систем сил, приложенных к твердому телу. Условия равновесия пространственной системы параллельных силНаправим ось 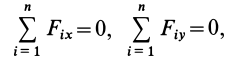 окажутся справедливыми для всех систем параллельных сил, т. е. превратятся в тождества. Момент относительно оси 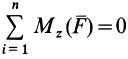 тоже выполняется для всех систем параллельных сил. Отбрасывая тоже выполняется для всех систем параллельных сил. Отбрасываяусловия равновесия, которые выполняются тождественно при выбранном направлении оси 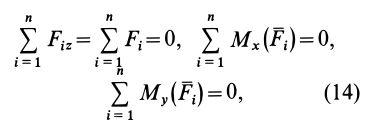  Рис. 37 т. е. для равновесия пространственной системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю. Условия равновесия плоской системы силРасположим оси 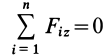 выполняется для всех плоских систем сил, т. е. является тождеством. Каждая из сил расположена в одной плоскости с осями координат выполняется для всех плоских систем сил, т. е. является тождеством. Каждая из сил расположена в одной плоскости с осями координат 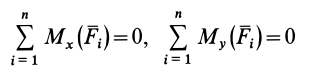 становятся тождествами. Моменты сил относительно оси 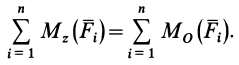 Из (13) для плоской системы сил после отбрасывания тождеств имеем следующие три условия равновесия: 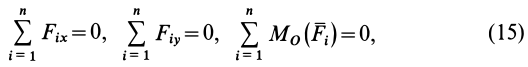 т. е. для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равна нулю.  Рис. 38 Для плоской системы параллельных сил (рис. 39) одну из осей координат, например 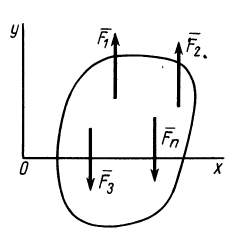 Рис. 39 Итак, для плоской системы параллельных сил из (15) имеем следующие условия равновесия:  т. е. для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма сил была равна нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости сил, также была равна нулю. Из условий равновесия плоской системы сил (15) можно получить и условия равновесия плоской системы сходящихся сил, для чего за моментную точку надо взять точку пересечения линий действия сходящихся сил. Тогда последнее из условий станет тождеством и в качестве условий равновесия для плоской системы сходящихся сил останутся только два первых условия из (15). |
