тесты геометрия 10 класс. !!!!!Тесты Геометрия 10. Тесты по геометрии для 10 класса 2013 г
 Скачать 341.47 Kb.
|
|
Подготовила: учитель математики Категория: высшая Тихончук Людмила Юрьевна Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №3» Станица Старощербиновская Щербиновского района Краснодарского края Тесты по геометрии для 10 класса 2013 г. Геометрия , как предмет, всегда представлялся ученикам сложным и непонятным. А курс стереометрии предъявляет к ученикам более высокие требования. С самого начала формулируются аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве и далее изучение свойств взаимного расположения прямых и плоскостей происходит на основе этих аксиом. Тем самым задается высокий уровень строгости и логических рассуждений, который должен выдержаться на протяжении всего курса. В работе представленные тесты помогут в изучении и закреплении этого материала. Ключи к тестам: 1.ТЕСТ ПО ТЕМЕ: « АКСИОМЫ СТЕРЕОМЕТРИИ И НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ АКСИОМ»
2.тест по теме: «Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости»
3.тест по теме: «Перпендикулярные прямые в пространстве. Перпендикулярность прямой и плоскости»
4.тест по теме: «Двугранный угол. Перпендикулярность плоскостей»
5.ТЕСТ ПО ТЕМЕ: «Перпендикуляр и наклонные. Теорема о трёх перпендикулярах».
6.ТЕСТ ПО ТЕМЕ : « ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ»
тест по теме: «Аксиомы стереометрии и некоторые следствия из них» Вариант 1 Уровень А 1. Какое утверждение неверное? 1) Через любые три точки проходит плоскость, и притом только одна. 2) Через две пересекающиеся прямые проходит плоскость, и притом только одна. 3) Через две параллельные прямые проходит плоскость, и притом только одна. 2. Параллелограмм ABCD лежит в плоскости  , если…1)  2)  3)  3. ABCDA1B1C1D1 – куб. Тогда плоскости (ABC) и (DD1C1)… 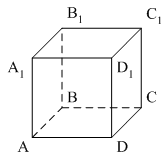 1) пересекаются; 2) не пересекаются; 3) совпадают. 4. Прямая MN не пересекает плоскость… 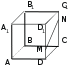 1) (ABC); 2) (AA1B1); 3) (BB1C1). 5. SABCD – четырёхугольная пирамида. Прямая SD не пересекает прямую… 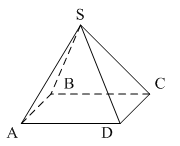 1) BC; 2) AD; 3) S. 6. Две различные плоскости не могут иметь… 1) общую точку; 2) общую прямую; 3) три общих точки, не лежащие на одной прямой. 7. Какое утверждение неверное? 1)  2)  3)  8. Через прямые m и k можно провести более одной плоскости. Тогда прямые m и k… 1) пересекаются; 2) параллельные; 3) совпадают. 9. Точка А принадлежит прямой а. Тогда через них можно провести… 1) хотя бы одну плоскость; 2) только одну плоскость; 3) не более одной плоскости. Уровень B 1. Точки A, B и С лежат на одной прямой, точка D не лежит на ней. Через каждые три точки проведена плоскость. Тогда число различных плоскостей равно… 2. Плоскости  и  пересекаются по прямой m. Точка А лежит в плоскости , точка В – в плоскости . Тогда прямая АВ лежит в плоскости , если…3. Проведены пять плоскостей. Каждые две из них пересекаются. Тогда наибольшее число прямых попарного пересечения плоскостей равно… 4. ABCD – параллелограмм. F 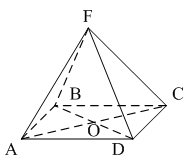 (ABC). Плоскости (AFC) и (BFD) пересекаются по прямой… тест по теме: «Аксиомы стереометрии и некоторые следствия из них» Вариант 2 Уровень A 1. Верно, что… 1) любые три точки лежат в одной плоскости; 2) любые четыре точки не лежат в одной плоскости; 3) через любые три точки, не лежащие на одной прямой, проходит плоскость, и при том только одна. 2. AB и CD – диаметры окружности с центром O. Все точки окружности лежат в плоскости , если…1)  2)  3)  3. Верно ли, что прямая лежит в плоскости данного треугольника, если она… 1) пересекает две стороны треугольника; 2) проходит через одну из вершин треугольника; 3) содержит одну из сторон треугольника. 4. ABCDA1B1C1D1 – куб. Тогда плоскости (AB1C1) и (СDD1)… 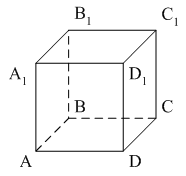 1) пересекаются; 2) не пересекаются; 3) совпадают. 5. Прямая MN не пересекает плоскость… 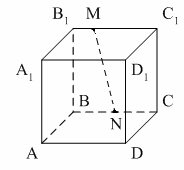 1) (АА1В1); 2) (ABC); 3) (AA1D1). 6. DABC – треугольная пирамида. Прямая BD непересекает прямую…  1) AC; 2) AD; 3) BC. 7. Сколько общих точек, не лежащих на одной прямой, не могут иметь две различные плоскости? 1) 1; 2) 2; 3) 3. 8. Даны две параллельные прямые a и b и точка M, не лежащая ни на одной из них. Точка M лежит в одной плоскости с прямыми a и b, если через точку M можно провести прямую, пересекающую… 1) хотя бы одну из данных прямых; 2) только одну из данных прямых; 3) две данные прямые. 9. Через три точки A, B и C можно провести единственную плоскость. Тогда точки… 1) не лежат на одной прямой; 2) лежат на одной прямой; 3) совпадают. |
