Поурочная по темам. поурочка. Урок , Порядок действий в вычислениях, 15. 10. 2021
 Скачать 459.68 Kb. Скачать 459.68 Kb.
|
5 класс, урок № , Порядок действий в вычислениях, 15.10.2021Цель урока: познакомить учащихся с порядком действий в вычислениях; учить применять это свойство при устных вычислениях.. Задачи: - научить учащихся работать с порядком действий при вычислениях - развить у них умение применять данные действия на практике - воспитать понимание свойств Ход урока I. Организационный момент 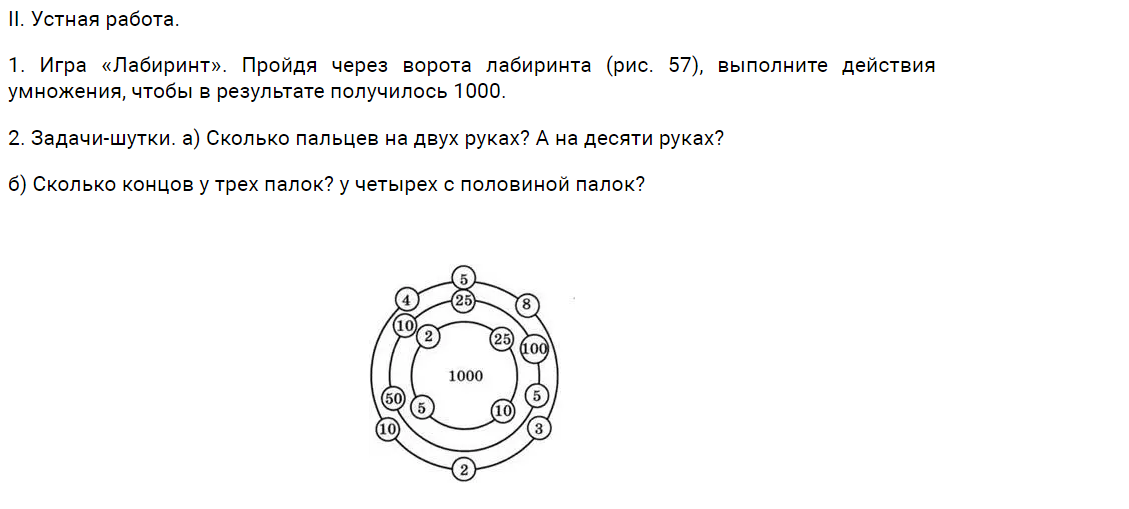  III. Актуализация знаний. Объяснение проводить согласно п. 3.3 учебника. 1. Числовые выражения. Значение числового выражения. 2. Порядок действий в выражениях без скобок, содержащих действия одной ступени. 3. Порядок действий в выражениях без скобок, содержащих действия разных ступеней. 4. Порядок действий в выражениях, содержащих скобки. Рассмотреть примеры, приведенные в пункте учебника. IV. Формирование умений и навыков. 1. У, № 268 (а, б, д, е). Контролировать промежуточные результаты при вычислении значений выражений. 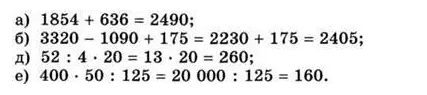 V. Итоги урока. 1. Расставьте в выражении скобки всеми возможными способами и найдите значение каждого выражения: 2 · 2 – 2 : 2. 2. Сформулируйте правила выполнения действий. VI. Домашнее задание. У, № 268 (в, г, ж, з), 280, 281. 7 класс, урок № , Медиана как статистическая характеристика, 15.10.2021Цель урока: познакомить учащихся с медианой .Зачади: - научить формуле медианы - развить у них понимание - воспитать ориентировку в статистической характеристике для нахождения медианы Ход урока I. Организационный момент II. Повторение и закрепление пройденного материала 1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач). 2. Контроль усвоения материала (письменный опрос). Вариант 1 1. Что такое среднее арифметическое ряда чисел? 2. Может ли ряд чисел иметь две моды? 3. Найдите среднее арифметическое, размах и моду ряда чисел: 16, 14, 11, 15, 14, 17. Вариант 2 1. Что такое мода ряда чисел? 2. Может ли среднее арифметическое ряда чисел не совпадать с одним из этих чисел? 3. Найдите среднее арифметическое, размах и моду ряда чисел: 12, 15, 11, 16, 11, 19. III. Работа по теме уроков Рассмотрим еще одну статистическую характеристику ряда чисел — медиану. Обсуждение начнем с такого примера. Пример 1 В ведомости приведены зарплаты (в тысячах рублей) 11 сотрудников фирмы: 14, 12, 16, 18, 14, 216, 15, 17, 20, 24, 19. Найдем среднее арифметическое этого ряда чисел: 385/11 = 35. Разумеется, эта величина плохо характеризует средний доход сотрудников фирмы (так как все сотрудники, кроме директора, получают значительно меньше). Мода такого ряда чисел, равная 14, также плохо характеризует доходы сотрудников фирмы. Поэтому приходится вводить новый статистический показатель данного ряда чисел — медиану. Упорядочим этот ряд чисел (например, в порядке возрастания чисел): 12, 14, 14, 15, 16, 17, 18, 19, 20, 24, 216. В середине ряда (на шестом месте) находится число 17, которое разумнее характеризует среднюю зарплату сотрудников фирмы. Такое число называют медианой ряда чисел. При этом, по сути дела, не учитываются резко отличающиеся от остальных числа. Теперь обсудим понятие медианы ряда чисел в случае их четного количества. Пример 2 Рассмотрим ряд, состоящий из 10 чисел: 14, 12, 16, 18, 14, 15, 17, 20, 24, 19. Как и в предыдущем примере, упорядочим этот ряд: 12, 14, 14, 15, 16, 17, 18, 19, 20, 24. На ближайших к середине ряда местах стоят: на пятом месте — число 16, на шестом месте — число 17. Тогда разумно считать, что полусумма этих чисел является медианой данного ряда чисел. Итак, для нахождения медианы ряда чисел надо упорядочить данный ряд чисел. 1. В ряду с нечетным числом членов медианой считается число, записанное посередине (стоящее в середине ряда). 2. В ряду с четным числом членов медианой считается число, равное полусумме чисел, записанных посередине. Заметим, что медиана разбивает ряд чисел на две одинаковые по численности группы: числа, не большие медианы, и числа, не меньшие медианы. В заключение отметим сложность статистической обработки данных в реальной жизни. Например, в качестве средней характеристики зарплаты в Москве можно принять любую из величин: среднее арифметическое, моду, медиану. Но, как видно из примера I, эти характеристики могут существенно различаться: среднее арифметическое равно 35, мода равна 14, и медиана равна 17. Какая из характеристик точнее отражает средний уровень зарплаты в Москве, остается вопросом. IV. Задания на уроках № 186 (а, в), 188 (б, в), 189, 191. V. Контрольные вопросы — Дайте определение медианы ряда чисел. — Может ли медиана ряда чисел не совпадать ни с одним из чисел ряда? — Какое число считают медианой упорядоченного ряда, содержащего нечетное количество чисел? четное количество чисел? VI. Подведение итогов уроков Домашнее задание № 186 (б, г), 188 (а, г), 190, 192, 193. 9 класс, урок № , Графики функций у = ах2 + n и у = а(х - m)2, 15.10.2021Цель урока: познакомить учащихся с графиком квадратичной функции .Зачади: - научить учащихся формуле квадратичной функции - развить у них понимание различий этих функций - воспитать ориентировку в квадратичной функции и ее переносе Ход урока Организационный момент I. Повторение и закрепление пройденного материала 1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач). 2. Контроль усвоения материала (письменный опрос). Вариант 1 1. Приведите основные свойства и график функции у = ах2 при а> 0. 2. Постройте график функции. 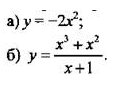 3. При каком значении а прямая у = х + а касается параболы y = 0,5x2? Вариант 2 1. Приведите основные свойства и график функции у = ах2 при а < 0. 2. Постройте график функции. 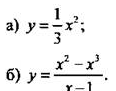 III. Изучение нового материала На предыдущем уроке были рассмотрены два важнейших преобразования графика функции у = f(x). 1. График функции у = -f(x) получается из графика функции у = f(x) с помощью симметрии относительно оси абсцисс. 2. График функции у = af(x) получается из графика функции у = f(x) растяжением вдоль оси ординат в а раз при а > 1 и сжатием в 1/a раз при 0 < а< 1. Эти преобразования пригодны для любых функций (как изученных, так и еще не рассмотренных). Поэтому необходимо знать такие преобразования и уметь ими пользоваться. Рассмотрим еще два важнейших преобразования графика функции у = f(х) - построение графиков функции у = f(х) + n и y = f(x - m). 3. График функции у = f(x) + n получается из графика функции у = f(x) с помощью параллельного переноса вдоль оси ординат на |n| единиц: вверх при n > 0 и вниз при n < 0. 1. Строим график функции у = х2. 2. Получаем из него график функции у = -х2 (преобразование 1 - симметрия относительно оси абсцисс). 3. Строим график функции у = -1/2х2 (преобразование 2 - сжатие предыдущего графика в два раза вдоль оси ординат). 4. Получаем из него график функции у = -1/2х2 + 1 (преобразование 3 - сдвиг на одну единицу вверх). 5. Строим график функции у = -1/2(х - 2)2 + 1 (преобразование 4- сдвиг предыдущего графика на две единицы вправо). После выполнения этих построений получаем окончательный график (на рисунке приведены: начальный этап построения - график функции у = х2 и конечный этап - график у = -1/2(х - 2)2 + 1). IV. Контрольные вопросы 1. Алгоритм построения графика функции у = -f(x)? 2. Как построить график функции у = af(x) при а > 0? 3. Построение графика функции у = f(x) + n. 4. Алгоритм построения графика функции у = f(x - m). V. Задание на уроке № 106 (а, в); 107 (а); 109 (а, в, д); 110 (б, в); 114; 116 (а, в); 117 (а); 118 (а, б). VI. Задание на дом № 106 (б, г); 107 (б); 109 (б, г, е); 110 (а, г); 115; 116 (б, г); 117 (б); 118 (в, г). VII. Подведение итогов урока 6 класс, урок № , Сравнение, сложение и вычитание дробей с разными знаменателями, 15.10.2021Цель урока: познакомить учащихся с работой с дробями .Зачади: - научить работе со знаминателями - развить у них понимание - воспитать ориентировку в нахождении НОК Ход урока I. Организационный момент     |
