Лекции по векторной алгебре. Векторная алгебра основные понятия и определения определение 1
 Скачать 1.31 Mb.
|
|
Гайлит Евгения Валерьевна Кандидат физико-математических наук, доцент Глава 2. векторная алгебра 2.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ Определение 1. Скалярной величиной или скаляром называется любое вещественное число. Определение 2. Величина, для задания которой необходимо указать ее численное значение и направление, называется векторной или вектором. Геометрическая модель вектора – прямолинейный направленный отрезок определенной длины. Направление фиксируется тем, что одна из конечных точек считается началом, а другая – концом. Векторы обозначаются  или  , где точки  и  являются соответственно началом и концом вектора.Определение 3. Численное значение вектора, т.е. расстояние между его началом и концом, называется длиной, или модулем, вектора и обозначается  или  .Определение 4. Нулевым вектором называется вектор, модуль которого равен нулю, а направление не определено (произвольно). Итак, если  – нулевой вектор, то  . Определение 5. Два вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых (обозначение  ). Определение 6. Три вектора называются компланарными, если они лежат на одной плоскости или на параллельных плоскостях. Определение 7. Два вектора равны (обозначение  ), если выполнены три условия: 1) = ; 2) ; 3)  и  одинаково направлены.Замечание 1. Условия 2 и 3 можно заменить одним: векторы  и сонаправлены (обозначение  ).Замечание 2. Из определения равенства векторов следует, что параллельное перемещение не меняет вектора. Этим свойством можно воспользоваться, например, чтобы привести векторы к общему началу. 2.2. Сложение векторов Пусть даны два вектора и .Рис.2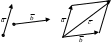.1  Определение. Суммой двух векторов и называется третий вектор  , который совпадает с диагональю параллелограмма, построенного на векторах и и имеющий с ними общее начало. Обозначение суммы векторов:  (рис.2.1).Это правило сложения двух векторов называется правилом параллелограмма. 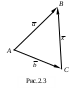 З 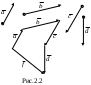 амечание 1. Из механики известно, что действие двух сил  и  на точку  тела равносильно действию одной силы  , их равнодействующей, определяемой по правилу параллелограмма. Таким образом,  .Замечание 2. Из определения следует, что имеет место переместительное свойство:   .Замечание 3. Если началом вектора  является конец вектора  , то сумму двух векторов и можно представить, как третий вектор  , начало которого совпадает с началом вектора , а конец – с концом вектора . Этот способ определения вектора называется правилом треугольника.Замечание 4. При сложении векторов имеет место сочетательное свойство  .Замечание 5. Сочетательное свойство позволяет найти сумму любого конечного числа векторов: для этого надо построить векторы так, чтобы конец предыдущего вектора был началом следующего. Вектор, замыкающий ломаную, построенную на этих векторах, началом которого является начало первого вектора, а концом – конец последнего, называется суммой заданных векторов. Например, вектор  (рис.2.2) есть сумма заданных векторов  и  : .Это правило называют правилом многоугольника. Замечание 6. Операция вычитания векторов есть действие, обратное сложению векторов: если  , то  . Для определения вектора  векторы  и  приводим к общему началу  так, чтобы  . На векторах  и  строим треугольник  . По правилу треугольника находим вектор (рис.2.3).2.3. Умножение вектора на скаляр Пусть  – вектор,  – скаляр.Определение 1. Произведением вектора на скаляр называется новый вектор  , который удовлетворяет трем условиям:1)  ;2)  ;3) вектор  однонаправлен с вектором при > 0 и противоположно направлен при < 0.Замечание 1. Условия 2 и 3 можно заменить следующим: вектор сонаправлен вектору , если > 0 и направлен противоположно, если  .Замечание 2. Из определения следует, что если  , то либо  , либо  .Умножение вектора на скаляр обладает следующими свойствами: 1)  ;2)  ;3)   ;4)  .Определение2. Ортом вектора называется вектор  единичной длины и соноправленный вектору , т.е.  и  .Замечание 3. Если – орт вектора  , то  .Определение3. Операции сложения векторов и умножение вектора на скаляр называются линейными. Определение4. Вектор  , где  – векторы;  – скаляры, называется линейной комбинацией векторов , скаляры  – коэффициентами линейной комбинации.2.4. Теоремы о разложении вектора по направлению данных векторов Теорема 1 (линейный случай). Если даны вектор и вектор  ему коллинеарный, то справедливо равенство  , где  скаляр.Доказательство. Если вектор  сонаправлен вектору , то  . Если  направлен противоположно вектору , то  . По определению произведения вектора на скаляр имеем .Теорема 2 (плоский случай). Если два вектора и не коллинеарные, то любой третий вектор , компланарный с ними, можно представить единственным образом как линейную комбинацию векторов и , т.е.  .Доказательство. Приведем три вектора 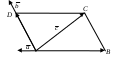, и к общему началу и построим параллелограмм, диагональю которого является вектор , а с тороны  и  лежат на одних прямых с векторами и (рис.2.4). По правилу параллелограммаРис.2.4 А  .  Заметим, что  и  . Отсюда ;  .  Подставляя  в  , получим .  Из построения следует, что разложение  единственно. |