ВОЛС. Оптическое волокно Сандугаш. Волоконнооптические
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
ВОЛОКОННО-ОПТИЧЕСКИЕ КОМПОНЕНТЫ СОВРЕМЕННЫХ СИСТЕМ ПЕРЕДАЧИ Как было отмечено выше, волоконно-оптические компоненты, включают пассивные компоненты, к которым относятся собственно оптические волокна, оптические соединители, изоляторы, ответвители и преобразователи длины волны, и активные компоненты, к которым относятся волоконно-оптические усилители (рис. 1.2). Общая структура разделов, посвященных данным компонентам, предусматривает рассмотрение основных теоретических положений, принципов функционирования и технических решений, которые используются в настоящее время при их создании, не углубляясь в область всего спектра возможных реализаций, что является важным в первую очередь для разработчиков этих устройств, и требует более тщательного анализа. В заключение рассмотрения каждого компонента будут приведены основные характеристики промышленных образцов, что на наш взгляд является необходимым для оценки возможности использования данных компонентов на стадии проектирования систем передачи и при анализе результатов измерений их параметров. 1.1. ОПТИЧЕСКОЕ ВОЛОКНО В физике хорошо известна двойственная (волновая и корпускулярная) природа света, на базе изучения свойств которой разработаны соответствующие теории, которые нельзя противопоставлять, так как лишь в своей совокупности они позволяют объяснить известные оптические явления. При этом волновая теория рассматривает свет как разновидность электромагнитных колебаний очень коротких (микрометровых) длин волн и использует при описании оптических процессов уравнения Максвелла. В то же время по корпускулярной теории свет представляется в виде быстро движущихся частиц, которые излучаются отдельными порциями (квантами), образуя луч света. Такая теория часто называется лучевой, и базируется она на известных законах геометрической оптики, позволяя наглядно и просто описывать распространение света в той или иной оптической среде, например в оптическом волноводе. Последний представляет собой круглый стержень из оптически прозрачного диэлектрика, который из-за малых размеров поперечного сечения обычно называют оптическим волокном (ОВ). ОВ широко используется в телекоммуникациях для передачи оптического излучения от источника к приемнику и является основным элементом оптического кабеля (ОК). Поскольку лучевая теория наглядно и достаточно просто описывает распространение света в оптическом волокне, в дальнейшем будем пользоваться аппаратом геометрической оптики. В тех же случаях, когда его применение недостаточно или невозможно, будем применять методы волновой теории. В физике хорошо известна двойственная (волновая и корпускулярная) природа света, на базе изучения свойств которой разработаны соответствующие теории, которые нельзя противопоставлять, так как лишь в своей совокупности они позволяют объяснить известные оптические явления. При этом волновая теория рассматривает свет как разновидность электромагнитных колебаний очень коротких (микрометровых) длин волн и использует при описании оптических процессов уравнения Максвелла.  Прохождение светового излучения через границу раздела сред В геометрической оптике световые волны изображаются лучами, которые претерпевают изменения на границах раздела сред с разными оптическими свойствами, характеризующимися показателем преломления 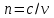 , который в общем случае показывает, во сколько раз скорость с распространения света в вакууме больше скорости V распространения света в рассматриваемой среде. Как известно, среда, у которой показатель преломления больше, называется оптически более плотной, в противном случае — менее плотной, поэтому при падении луча света (световой волны) на границу раздела таких сред в общем случае появляются отраженная и преломленная волны (рис. 1.За), причем в соответствии с законом Снеллиуса углы , который в общем случае показывает, во сколько раз скорость с распространения света в вакууме больше скорости V распространения света в рассматриваемой среде. Как известно, среда, у которой показатель преломления больше, называется оптически более плотной, в противном случае — менее плотной, поэтому при падении луча света (световой волны) на границу раздела таких сред в общем случае появляются отраженная и преломленная волны (рис. 1.За), причем в соответствии с законом Снеллиуса углы 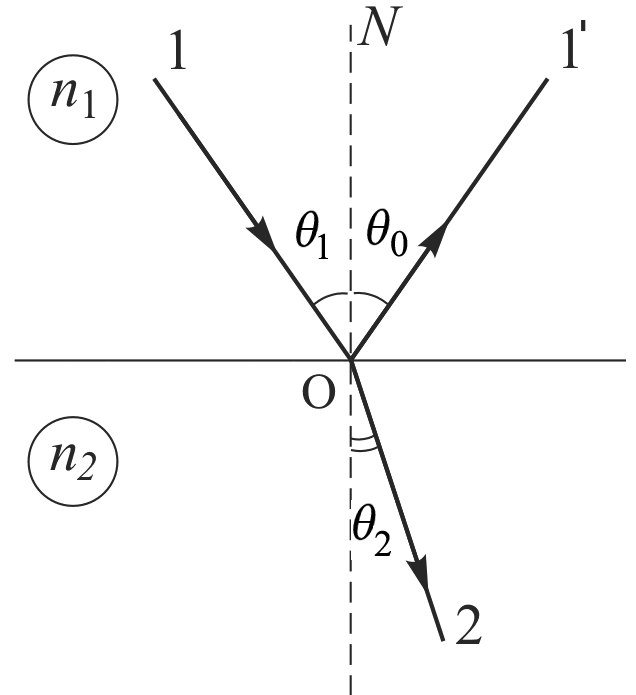 Рис. 1.3а. Отражение и преломление светового луча на границе двух сред Рис. 1.3а. Отражение и преломление светового луча на границе двух сред  Рис. 1,3 Полное внутреннее отражение светового луча на границе двух сред 1.1.2. Распространение световых лучей в оптических волокнах В общем случае оптическое волокно (рис. 1.4) состоит из сердцевины, по которой происходит распространение световых волн, и оболочки, предназначенной, с одной стороны, для создания лучших условий отражения на границе раздела “сердцевина — оболочка", а с другой — для снижения излучения энергии в окружающее пространство. С целью повышения прочности и тем самым надежности волокна на поверх оболочки, как правило, накладывается первичное защитное упрочняющее покрытие такая конструкция ОВ является типовой и используется во многих ОВ в качестве базовой. Рис. 1,3 Полное внутреннее отражение светового луча на границе двух сред 1.1.2. Распространение световых лучей в оптических волокнах В общем случае оптическое волокно (рис. 1.4) состоит из сердцевины, по которой происходит распространение световых волн, и оболочки, предназначенной, с одной стороны, для создания лучших условий отражения на границе раздела “сердцевина — оболочка", а с другой — для снижения излучения энергии в окружающее пространство. С целью повышения прочности и тем самым надежности волокна на поверх оболочки, как правило, накладывается первичное защитное упрочняющее покрытие такая конструкция ОВ является типовой и используется во многих ОВ в качестве базовой.  1.1.2.1. Основы лучевой теории распространения света в ОВ Как было отмечено выше, лучи света распространяются в ОВ при выполнении условий 1.1.2.1. Основы лучевой теории распространения света в ОВ Как было отмечено выше, лучи света распространяются в ОВ при выполнении условий  в связи с чем для характеристики волокна используется соотношение, которое принято характеризовать относительной разностью показателей преломления ∆ в связи с чем для характеристики волокна используется соотношение, которое принято характеризовать относительной разностью показателей преломления ∆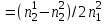 и которое для большинства ОВ равно ∆=10 и которое для большинства ОВ равно ∆=10 . При этом если показатель преломления оболочки имеет постоянное значение, то показатель преломления сердцевины может быть либо постоянным, либо изменяться вдоль радиуса по определенному закону. Характер изменения показателя преломления ОВ вдоль радиуса называется профилем показателя преломления. Так, для произвольного степенного изменения профиля показателя преломления закон изменения n(r) по радиусу определяется выражением . При этом если показатель преломления оболочки имеет постоянное значение, то показатель преломления сердцевины может быть либо постоянным, либо изменяться вдоль радиуса по определенному закону. Характер изменения показателя преломления ОВ вдоль радиуса называется профилем показателя преломления. Так, для произвольного степенного изменения профиля показателя преломления закон изменения n(r) по радиусу определяется выражением 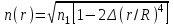 (1.2) где r - текущий радиус; R - радиус сердцевины; (1.2) где r - текущий радиус; R - радиус сердцевины;  показатель преломления в центре сердцевины, равный примерно 1,5; q ={1, показатель преломления в центре сердцевины, равный примерно 1,5; q ={1, } - показатель степени, определяющий изменение n(r); ∆=0.00З - 0.01. Очевидно, что при q= } - показатель степени, определяющий изменение n(r); ∆=0.00З - 0.01. Очевидно, что при q= профиль показателя преломления определяется как профиль показателя преломления определяется как 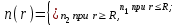 (1.3) и соответствует ступенчатому волокну, а при q = 2 - волокну с наиболее распространенным параболическим профилем показателя преломления, для которого (1.3) и соответствует ступенчатому волокну, а при q = 2 - волокну с наиболее распространенным параболическим профилем показателя преломления, для которого 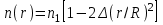 (1.4) Выбор соотношения между п, и п, определяется различными факторами в зависимости от назначения и области применения ОВ. Кроме того, ступенчатые ОВ могут иметь и несколько отражающих оболочек, например, так называемое волокно W - типа, с сердцевиной из материала с показателем преломления (1.4) Выбор соотношения между п, и п, определяется различными факторами в зависимости от назначения и области применения ОВ. Кроме того, ступенчатые ОВ могут иметь и несколько отражающих оболочек, например, так называемое волокно W - типа, с сердцевиной из материала с показателем преломления  окруженной двумя оболочками, первая из которых имеет показатель преломления окруженной двумя оболочками, первая из которых имеет показатель преломления  , а вторая , а вторая  , причем , причем  › › › ›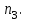 Процесс распространения световых лучей в оптически более плотной среде, окруженной менее плотной, в рамках геометрической оптики, показан на рис. 1.5. При попадании светового излучения на торец ОВ в нем могут распространяться три типа световых лучей на торец волокна, угле ввода Процесс распространения световых лучей в оптически более плотной среде, окруженной менее плотной, в рамках геометрической оптики, показан на рис. 1.5. При попадании светового излучения на торец ОВ в нем могут распространяться три типа световых лучей на торец волокна, угле ввода  оптического излучения в ОВ и их дальнейшем попадании на границу раздела на ней может иметь место полное внутреннее отражение. Те лучи, которые падают на границу раздела под углом оптического излучения в ОВ и их дальнейшем попадании на границу раздела на ней может иметь место полное внутреннее отражение. Те лучи, которые падают на границу раздела под углом 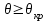 (лучи 1, 2 и 3 )‚ отражаются от нее и вновь возвращаются в сердцевину волокна, распространяясь в ней и не претерпевая преломления. Так как траектории таких лучей полностью расположены внутри среды распространения — сердцевины волокна, они распространяются на большие расстояния и называются направляемыми, являясь основным типом лучей в сердцевине ОВ (лучи 1, 2 и 3 )‚ отражаются от нее и вновь возвращаются в сердцевину волокна, распространяясь в ней и не претерпевая преломления. Так как траектории таких лучей полностью расположены внутри среды распространения — сердцевины волокна, они распространяются на большие расстояния и называются направляемыми, являясь основным типом лучей в сердцевине ОВ 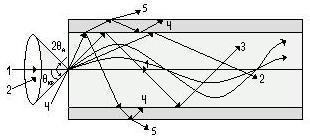 Лучи, падающие на границу раздела под углами Лучи, падающие на границу раздела под углами 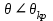 (лучи 4), носят название вытекающих лучей (лучей оболочки). Достигая границы “сердцевина — оболочка”, эти лучи отражаются и преломляются, теряя каждый раз в оболочке волокна, часть энергии, в связи, с чем исчезают вовсе на некотором расстоянии от торца волокна. Те же лучи, которые излучаются из оболочки в окружающее пространство (лучи 5), носят название излучаемых лучей. Они, естественно, не распространяются вдоль ОВ, а, как правило, возникают в местах нерегулярностей волокна. Очевидно, что излучаемые и вытекающие волны— это паразитные волны, приводящие к рассеиванию энергии и искажению информационного сигнала. 1.1.2.2. Характеристики направляемых лучей Для характеристики направляемого луча с точки зрения геометрической оптики необходимо определить траекторию его распространения, которая для ступенчатого волокна может быть либо меридианной, пересекающей ось волокна между точками отражений, либо косой, не пересекающей ось. В зависимости от данных траекторий следует различать меридианные и косые световые лучи. Таким образом, меридианные лучи характеризуются углом падения, образованным лучом и нормалью к оси волокна. Между соседними точками отражений данные лучи распространяются по прямой линии, а направление луча после отражения определяется законом Снеллиуса. В результате траектория меридианного луча лежит в плоскости, проходящей через ось волокна, и имеет зигзагообразный вид. Косые лучи распространяются по спиралеобразной траектории, проекция которой на поперечное сечение волокна имеет вид правильного незамкнутого треугольника. Поэтому для определения косого луча кроме угла падения необходимо знать второй угол, который характеризует скос луча и определяется как угол в плоскости сечения сердцевины между касательной к границе раздела и проекцией траектории луча. Для характеристики меридианных лучей, направляемых под углом (лучи 4), носят название вытекающих лучей (лучей оболочки). Достигая границы “сердцевина — оболочка”, эти лучи отражаются и преломляются, теряя каждый раз в оболочке волокна, часть энергии, в связи, с чем исчезают вовсе на некотором расстоянии от торца волокна. Те же лучи, которые излучаются из оболочки в окружающее пространство (лучи 5), носят название излучаемых лучей. Они, естественно, не распространяются вдоль ОВ, а, как правило, возникают в местах нерегулярностей волокна. Очевидно, что излучаемые и вытекающие волны— это паразитные волны, приводящие к рассеиванию энергии и искажению информационного сигнала. 1.1.2.2. Характеристики направляемых лучей Для характеристики направляемого луча с точки зрения геометрической оптики необходимо определить траекторию его распространения, которая для ступенчатого волокна может быть либо меридианной, пересекающей ось волокна между точками отражений, либо косой, не пересекающей ось. В зависимости от данных траекторий следует различать меридианные и косые световые лучи. Таким образом, меридианные лучи характеризуются углом падения, образованным лучом и нормалью к оси волокна. Между соседними точками отражений данные лучи распространяются по прямой линии, а направление луча после отражения определяется законом Снеллиуса. В результате траектория меридианного луча лежит в плоскости, проходящей через ось волокна, и имеет зигзагообразный вид. Косые лучи распространяются по спиралеобразной траектории, проекция которой на поперечное сечение волокна имеет вид правильного незамкнутого треугольника. Поэтому для определения косого луча кроме угла падения необходимо знать второй угол, который характеризует скос луча и определяется как угол в плоскости сечения сердцевины между касательной к границе раздела и проекцией траектории луча. Для характеристики меридианных лучей, направляемых под углом 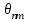 к оси ОВ, обычно вводятся следующие параметры [2]: длина пути к оси ОВ, обычно вводятся следующие параметры [2]: длина пути  определяемая расстоянием между двумя последовательными отражениями: определяемая расстоянием между двумя последовательными отражениями:  (1.5) оптическая длина пути (1.5) оптическая длина пути  определяемая для однородной среды выражением определяемая для однородной среды выражением 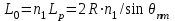 (1.6) полупериод траектории луча Ьд, представляющий собой расстояние между точками двух последовательных отражений вдоль оси волокна, равный (1.6) полупериод траектории луча Ьд, представляющий собой расстояние между точками двух последовательных отражений вдоль оси волокна, равный  (1.7) И число отражений N на единицу длины среды распространения, равное (1.7) И число отражений N на единицу длины среды распространения, равное 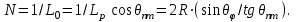 (1.8) При описании траектории распространяемого в волокне косого луча, представляющего собой луч со спиральной траекторией, лучевые параметры для косых траекторий принимают вид: длина пути (1.8) При описании траектории распространяемого в волокне косого луча, представляющего собой луч со спиральной траекторией, лучевые параметры для косых траекторий принимают вид: длина пути 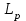 , определяемая расстоянием между двумя последовательными отражениями , определяемая расстоянием между двумя последовательными отражениями  (1.9) Оптическая длина пути, (1.9) Оптическая длина пути,  определяемая ДЛЯ однородной среды выра- жением определяемая ДЛЯ однородной среды выра- жением  (1.10) число отражений N на единицу длины среды распространения, равное (1.10) число отражений N на единицу длины среды распространения, равное 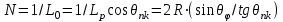 (1.11) Последнее, как следует из выражения, связано с полупериодом траектории (1.11) Последнее, как следует из выражения, связано с полупериодом траектории  луча — расстоянием между точками двух последовательных отражений среды по оси ОВ. Здесь луча — расстоянием между точками двух последовательных отражений среды по оси ОВ. Здесь 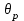 , - угол, характеризующий скос луча, который определяется как угол в плоскости сечения сердцевины между касательной к границе раздела и проекцией траектории луча. Учитывая, что скорость распространения света у для среды с показа- телем преломления , - угол, характеризующий скос луча, который определяется как угол в плоскости сечения сердцевины между касательной к границе раздела и проекцией траектории луча. Учитывая, что скорость распространения света у для среды с показа- телем преломления  определяется как определяется как 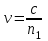 (1.12) где с - скорость света в вакууме, время t прохождения луча на расстоя- ние (1.12) где с - скорость света в вакууме, время t прохождения луча на расстоя- ние  в обоих случаях равно в обоих случаях равно  (1.13) Отсюда следует важный вывод, что условие (1.13) Отсюда следует важный вывод, что условие 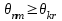 , для меридианных оптических лучей и д,“ гдт для косых лучей будет отличаться, т. е. , для меридианных оптических лучей и д,“ гдт для косых лучей будет отличаться, т. е. , так как закон Снеллиуса справедлив для отражения от плоской поверхности, в то время как поверхность волокна искривлена. Кроме того, время прохождения луча не зависит от угла скоса, а определяется только значением угла падения 0„ световой волны на границу волокна. 1.1.2.3. Апертура оптического волокна Как следует из выше изложенного, существует бесконечное множество лучей, которые, будучи введенными в ОВ под углом , так как закон Снеллиуса справедлив для отражения от плоской поверхности, в то время как поверхность волокна искривлена. Кроме того, время прохождения луча не зависит от угла скоса, а определяется только значением угла падения 0„ световой волны на границу волокна. 1.1.2.3. Апертура оптического волокна Как следует из выше изложенного, существует бесконечное множество лучей, которые, будучи введенными в ОВ под углом 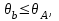 , в дальнейшем, при распространении по волокну, имеют , в дальнейшем, при распространении по волокну, имеют  . Следовательно, для обеспечения условия полного внутреннего отражения при распространении световых лучей необходимо обеспечить ввод излучения в торец ОВ подуглом, меньшим или равным . Следовательно, для обеспечения условия полного внутреннего отражения при распространении световых лучей необходимо обеспечить ввод излучения в торец ОВ подуглом, меньшим или равным 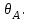 . Угол . Угол  между оптической осью и одной из образующих светового конуса — лучей, падающих в торец ОВ (рис. 1.5), для которых в дальнейшем выполняется условие полного внутреннего отражения, носит название апертура ОВ. Физически апертура характеризует эффективность ввода оптического излучения в ОВ, а для ее числовой оценки используется понятие номинальной числовой апертуры (NUMERICAL APERTURE), значение которой для ступенчатого оптического волокна определяется выражением [З] между оптической осью и одной из образующих светового конуса — лучей, падающих в торец ОВ (рис. 1.5), для которых в дальнейшем выполняется условие полного внутреннего отражения, носит название апертура ОВ. Физически апертура характеризует эффективность ввода оптического излучения в ОВ, а для ее числовой оценки используется понятие номинальной числовой апертуры (NUMERICAL APERTURE), значение которой для ступенчатого оптического волокна определяется выражением [З] 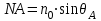 (1.14) где (1.14) где  - показатель преломления окружающей среды, равный для воздуха - показатель преломления окружающей среды, равный для воздуха  =1. В соответствии с законом Снеллиуса можно записать =1. В соответствии с законом Снеллиуса можно записать  (1.15) и, учитывая, что (1.15) и, учитывая, что  (1‚16) выражение для номинальной числовой апертуры примет вид (1‚16) выражение для номинальной числовой апертуры примет вид  (1-17) Из последнего выражения видно, что с увеличением разности показа- телей преломления сердцевины и оболочки значение NA возрастает и, следовательно, улучшается эффективность ввода излучения в ОВ. На- пример, при (1-17) Из последнего выражения видно, что с увеличением разности показа- телей преломления сердцевины и оболочки значение NA возрастает и, следовательно, улучшается эффективность ввода излучения в ОВ. На- пример, при  и и  =1.13 все меридианные лучи, падающие из возду- ха на торец ОВ, входят в сердцевину ( =1.13 все меридианные лучи, падающие из возду- ха на торец ОВ, входят в сердцевину ( ) Последнее выражение учитывает только меридианные лучи, в то время как в ОВ в основном имеют место косые лучи с гораздо более сложно траекторией распространения, расчет ввода которых гораздо сложнее. Поэтому получить простое выражение для числовой апертуры косых лучей не удается. Однако здесь необходимо отметить, что апертура, полученная по данному выражению для меридианных лучей ступенчатого ОВ, меньше действительной апертуры, учитывающей все введенные лучи. Для градиентных ОВ вводится понятие локальной числовой апертуры, равной ) Последнее выражение учитывает только меридианные лучи, в то время как в ОВ в основном имеют место косые лучи с гораздо более сложно траекторией распространения, расчет ввода которых гораздо сложнее. Поэтому получить простое выражение для числовой апертуры косых лучей не удается. Однако здесь необходимо отметить, что апертура, полученная по данному выражению для меридианных лучей ступенчатого ОВ, меньше действительной апертуры, учитывающей все введенные лучи. Для градиентных ОВ вводится понятие локальной числовой апертуры, равной  (1.18) которая показывает, что максимальный угол ввода оптического излучения в этом случае определяется тем, в какой точке сердцевины волокна находится вершина конуса, иными словами, захват волокном вводимого луча света зависит от того, в какой точке сердцевины он вводится в градиентное волокно. Очевидно, что при r = 0, т. е. при вводе излучения по оси волокна, локальная числовая апертура равна номинальной числовой апертуре. Для наиболее распространенного градиентного ОВ с параболическим профилем показателя преломления числовая апертура определяется выражением (1.18) которая показывает, что максимальный угол ввода оптического излучения в этом случае определяется тем, в какой точке сердцевины волокна находится вершина конуса, иными словами, захват волокном вводимого луча света зависит от того, в какой точке сердцевины он вводится в градиентное волокно. Очевидно, что при r = 0, т. е. при вводе излучения по оси волокна, локальная числовая апертура равна номинальной числовой апертуре. Для наиболее распространенного градиентного ОВ с параболическим профилем показателя преломления числовая апертура определяется выражением  (1.19) Естественно, что определение числовой апертуры косых лучей градиентного волокна представляет еще более сложную задачу, нежели в случае ступенчатого. В заключение следует отметить, что равенство числовых апертур источника и приемника излучения является одним из необходимых усло- вий достижения малых потерь при их соединении. (1.19) Естественно, что определение числовой апертуры косых лучей градиентного волокна представляет еще более сложную задачу, нежели в случае ступенчатого. В заключение следует отметить, что равенство числовых апертур источника и приемника излучения является одним из необходимых усло- вий достижения малых потерь при их соединении. |
