Ответы на экзаменационные вопросы. Вопросы по курсу "Теплопередача"
 Скачать 329.5 Kb.
|
|
Вопросы по курсу "Теплопередача" 1. Механизмы переноса теплоты. Основные виды теплообмена Теплопроводность. Температурное поле. Гипотеза Фурье. Теплоотдача и теплопередача. Коэффициенты теплоотдачи и теплопередачи, их физический смысл. ОТВЕТ Сложный процесс переноса теплоты разбивают на ряд более простых: теплопроводность, конвекция и теплообмен излучением. Такой прием упрощает его изучение. Кроме того, как будет показано ниже, каждый простой процесс переноса теплоты подчиняется своим законам. Различают молекулярный и конвективный механизмы переноса теплоты. Молекулярный перенос теплоты осуществляется посредством теплового движения микрочастиц в среде с неоднородным распределением температуры. Конвективный перенос теплоты осуществляется в среде с неоднородным распределением скорости и температуры макроскопическими элементами среды при их перемещении. Теплопроводностью называют молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры, [уравнение (1. 3)]. Конвективным теплообменом называют процесс, обусловленный совместным действием конвективного и молекулярного переносов теплоты. В инженерной практике большое значение имеет частный случай этого способа переноса теплоты, а именно теплоотдача. Теплоотдачей называют конвективный теплообмен между движущейся средой и поверхностью ее раздела с другой средой: твердым телом, жидкостью или газом. Теплообмен излучением — это процесс, который происходит следующим образом: внутренняя энергия вещества превращается в энергию излучения (энергия фотонов или электромагнитных волн, излучаемых телом или средой), далее происходит распространение излучения в пространстве (процесс переноса излучения), далее энергия излучения поглощается веществом, которое оказалось на пути фотонов или электромагнитных волн. В природных объектах и инженерных сооружениях теплота переносится всеми тремя способами одновременно — такой процесс называется теплопередачей. Во многих случаях удается выделить способ, на который приходится большая часть перенесенной теплоты, и поэтому упростить метод определения ее количества. В тех случаях, когда это сделать не удается, задача усложняется. Теплопередача связана с весьма сложными процессами и при ее изучении надо знать законы и методы анализа, применяемые в физике, термодинамике, гидрогазодинамике и химии. Теплопроводность это важнейшая техническая характеристика теплоизоляционного материала. Количественно теплопроводность определяется коэффициентом теплопроводности (λ), выражающим количество тепла, проходящее через образец материала толщиной 1 м и площадью 1 м2 при разности температур на противолежащих поверхностях 1°К за 1 час. На величину теплопроводности теплоизоляционных материалов оказывают влияние плотность материала, вид, размеры и расположение пор (пустот) и т.д. Сильное влияние оказывает также температура материала и, особенно, его влажность. Теплопроводность вакуума - 0, то есть вакуум не проводит тепло. Это абсолютный теплоизолятор. Теплопроводность воздуха зависит от его температуры и давления. В большинстве житейских случаев она колеблется возле отметки 0.02 Вт/(м*K). Теплопроводность снега зависит от его состояния. Если он только что выпал, то его теплопроводность примерно равна 0.10-0.15 Вт/(м*K), а если уже слежался, то 0.25-0.4 Вт/(м*K). Температурным полем называется совокупность значений t˚ во всех точках рассматриваемого пространства (ТВ тела) в каждый фиксированный момент времени. t=f(x,y,z,τ) (1) в данном случае температура – это скалярная величина, определяющая степень нагретости тела в каждой точке. Различают стационарное и нестационарное температурные поля. Ф-ла (1) относится к неустановившемуся тепловому режиму и называется нестационарным тепловым полем. Если тепловой режим явл установившемся, то температура в каждой точке тела с течением времени не меняется, изменяясь лишь от точек к точкам с разными координатами, такое температурно поле наз стационарным и t˚ явл функцией координат по пространству t=f(x,y,z) ;∂T⁄∂τ=0 Согласно гипотезе Фурье количество теплоты dQτ, Дж, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту ∂t⁄∂n: Коэффициент теплопередачи является количественной расчетной величиной и зависит от коэффициентов теплоотдачи, термического сопротивления стенки и загрязнений. Для плоской стенки 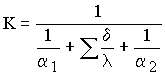 , (9.28)где  – коэффициент теплоотдачи от горячего теплоносителя, Вт/(м град);  – толщина теплопередающей стенки аппарата, м;  - коэффициент теплопроводности материала стенки, Вт/(м град);  - коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м град);  – термическое сопротивление загрязнения стенки, м2 град/Вт.Коэффициент теплоотдачи  показывает, какое количество теплоты передаётся от горячего теплоносителя к холодному через 1 м2 поверхности при средней разности температур в 1 градус за 1 с:  Коэффициент теплоотдачи зависит от: - скорости жидкости  , её плотности  и вязкости  , т.е. переменных определяющих режим течения жидкости,- тепловых свойств жидкости (удельной теплоёмкости ср, теплопроводности  ), а также коэффициента объёмного расширения  ,- геометрических параметров – формы и определяющих размеров стенки (для труб – их диаметр d и длина L), а также шероховатости  стенки. Вследствие сложной зависимости коэффициента теплоотдачи от большого числа факторов невозможно получить расчётное уравнение для , пригодное для всех случаев теплоотдачи, поэтому для расчётов используют обобщённые (критериальные) уравнения для типовых случаев теплоотдачи.2. Уравнение энергии. Уравнение Фурье-Кирхгофа (с выводом). ОТВЕТ: Для определения коэффициента теплоотдачи 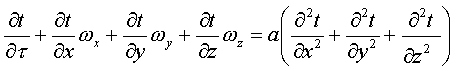необходимо знать температурный градиент жидкости у стенки, т.е. распределение температур в жидкости. Исходной зависимостью для обобщения опытных данных по теплоотдаче является общий закон распределения температур в жидкости, выражаемый дифференциальным уравнением конвективного теплообмена, которое носит название уравнение Фурье-Кирхгофа: где  ,  где - теплопроводность,с – теплоёмкость, - плотность.Дифференциальное уравнение конвективного теплообмена или уравнение Фурье-Кирхгофа:  Коэффициент температуропроводности характеризует тепловую инерционность тела, т.е. сравнивает скорость распространения теплоты (температуры) в различных средах (при прочих равных условиях быстрее нагреется и охладится то тело, которое обладает большим коэффициентом температуропроводности).Для твёрдых тел  Следовательно,  При установившемся процессе теплообмена  Для практического использования уравнения Фурье-Кирхгофа его представляют в виде функции от критерия подобия. 3. Динамическое уравнение движения (уравнение Навье-Стокса). Уравнение сплошности. (неразрывности движения). Их физический смысл. ОТВЕТ: Уравнения Навье — Стокса (англ. Navier-Stokes) — система дифференциальных уравнений в частных производных, описывающая движение и теплопередачу вязкой жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Анри Навье и британского математика Джорджа Стокса. Система состоит из трех уравнений: уравнения теплопроводности, уравнения неразрывности, уравнения движения. В векторном виде для несжимаемой жидкости они записываются следующим образом:    где:  - оператор Гамильтона, Δ - оператор Лапласа,  - вектор скорости, t - время, ν - коэффициент кинематической вязкости, ρ - плотность, P - давление,  - вектор плотности массовых сил, T - температура, cp - теплоемкость при постоянном давлении...4. Основное уравнение теории теплопроводности (уравнение Фурье) и его физический смысл. Краевые условия. Задачи о температурном поле твердого тела, условия первого, второго и третьего рода. ОТВЕТ: Количество теплоты, передаваемой от горячего теплоносителя, прямо пропорционально площади теплопередающей поверхности F, действующей средней разности температур Δt, продолжительности процесса τ и коэффициенту теплоотдачи : Коэффициент теплоотдачи показывает, какое количество теплоты передаётся от горячего теплоносителя к холодному через 1 м2 поверхности при средней разности температур в 1 градус за 1 с:Коэффициент теплоотдачи зависит от: - скорости жидкости , её плотности и вязкости , т.е. переменных определяющих режим течения жидкости,- тепловых свойств жидкости (удельной теплоёмкости ср, теплопроводности ), а также коэффициента объёмного расширения ,- геометрических параметров – формы и определяющих размеров стенки (для труб – их диаметр d и длина L), а также шероховатости стенки.Вследствие сложной зависимости коэффициента теплоотдачи от большого числа факторов невозможно получить расчётное уравнение для , пригодное для всех случаев теплоотдачи, поэтому для расчётов используют обобщённые (критериальные) уравнения для типовых случаев теплоотдачи.Краевые условия (условия однозначности) включают в себя:
Геометрическими условиями задаются форма и линейные размеры тела, в котором протекает процесс. Физическими условиями задаются физические параметры тела (c, λ, ρ и др) и может быть задан закон распределения внутренних источников теплоты. Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано следующим образом (при τ=0) : t=f(x,y,z) при равномерном распределении температуры в теле начальное условие упрощается (при τ=0) : t=to=const Граничные условия могут быть заданы несколькими способами. Граничные условия I рода. Задается распределение температуры на поверхности тела для каждого момента времени. tс=f(x,y,z,τ) tс – температура на поверхности тела. В частном случае, когда температура на поверхности тела является постоянной на протяжении всего времени протекания процесса теплообмена, уравнение упрощается и принимает вид tс=const Граничные условия II рода. Задаются значения теплового потока для каждой точки поверхности тела и любого момента времени. qп=f(x,y,z,τ) qп- плотность теплового потока. В простейшем случае: qп=qo=const Граничные условия III рода. Задаются температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. Согласно закону Ньютона-Рихмана количество теплоты, отдаваемое единицей поверхности тела в единицу времени, пропорционально разности температур поверхности тела tc и окружающей среды tж (tc>tж) q=α(tс-tж) где α – коэффициент пропорциональности, называемый коэффииентом теплоотдачи, Вт/(м²*К), характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоты, отдаваемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу. q=-λ(∂t⁄∂n)c отсюда окончательно граничное условие III рода : (∂t⁄∂n)c=- (α/λ)(tс-tж) 5. Решение задачи определения температурного поля плоской однослойной стенки стационарном режиме в граничных условиях первого рода. Многослойная плоская стенка. Тепловой поток через однослойную и многослойную плоскую стенку. ОТВЕТ: Теплопередача через многослойную плоскую пластину Теплопередача-теплообмен между двумя теплоносителями через твердое тело Q’ –тепловой поток, который подводится от теплоносителя к твердому телу 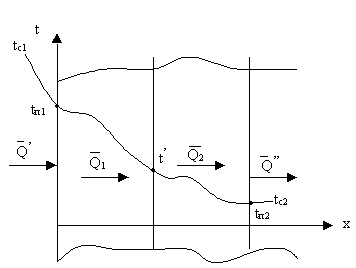 В стационарном случае при отсутствии источников теплоты Для тепловых потоков справедливо:  [Дж]Q’=Q1=Q2=…=Qn=Q’’ [Вт] Для плотности тепловых потоков q’= q1=…=qn=q’’ [Вт/м2] в сплошных телах площадь теплообмена переменна, поэтому плотности потоков будут различаться q’= б1*( tc1- tп1) q1=-л*gradt= б*( tп1-t’)/д … q’’= б*( tп1- tс2) получили систему n+2 уравнений (n-количество слоев) с n+2 неизвестными => система имеет единственное решение t  c1- tп1=q/б1tп1-t’= (д1/л1)*q + => tc1- tс2=q(1/ б1+ д1/л1+…+1/б2) 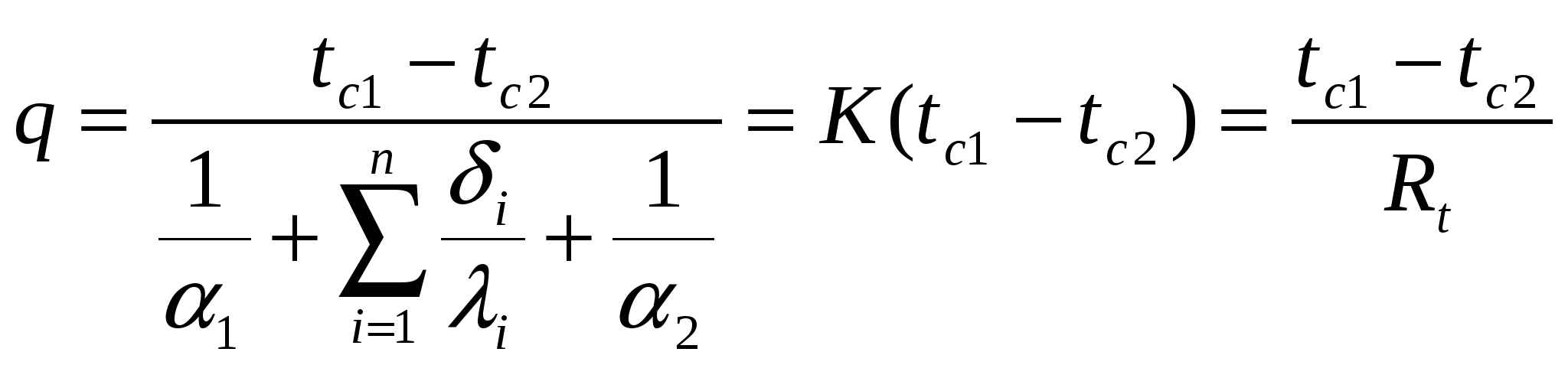 tп1- tс2=q/б2 неизвестные температуры находятся последовательной подстановкой q в уравнения системы. |