Прикладная математика. Задача 1 (Линейная производственная задача) Задача 2 Двойственная задача

• Название: Задача 1 (Линейная производственная задача) Задача 2 Двойственная задача
• Дата: 09.06.2022
• Размер: 439 Kb.
• Имя файла: Прикладная математика.doc
• Тип: Задача; #580537
• страница: 1 из 3

Содержание.

1. 
   Задание на курсовой проект……………………………………………………...2
   
2. 
   Задача №1 (Линейная производственная задача).………………………….4
   
3. 
   Задача №2
   
   1. 
      Двойственная задача………………………………………………………7
      
   2. 
      Задача о "расшивке узких мест производства"………………………..8
      
4. 
   Сводная таблица результатов по задачам №1 и №2………………..……..11
   
5. 
   Задача №3 (Транспортная задача)………………………………...…………..12
   
6. 
   Задача №4 (Динамическое программирование)…………………………….15
   
7. 
   Задача №5 (Динамическая задача управления производством и запасами)…………………………………………………………………………...18
   

Задание на курсовОЙ ПрОЕКТ.

1. 
   Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А затрат различных ресурсов на единицу каждой продукции, вектор объемов ресурсов В и вектор удельной прибыли С при возможном выпуске четырех видов продукции с использованием трех видов ресурсов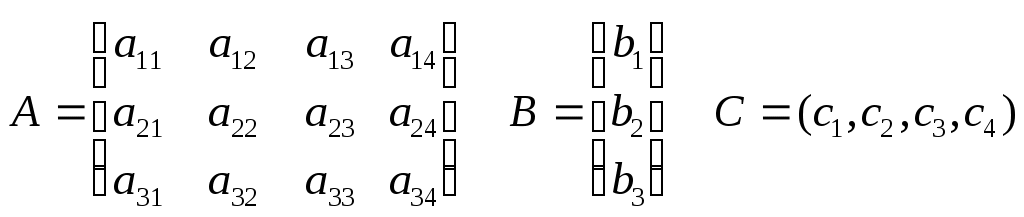
   

компактно записаны в виде

c₁ c₂ c₃ c₄

а₁₁ а₁₂ а₁₃ а₁₄ b₁

a₂₁ a₂₂ a₂₃ a₂₄ b₂

a₃₁ a₃₂ a₃₃ a₃₄ b₃
Преобразовать данную задачу к виду основной задачи линейного программирования, решить ее методом направленного перебора базисных допустимых решений, обосновывая каждый шаг процесса, найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов различных видов и указать узкие места производства.

В последней симплексной таблице указать обращенный базис Q^-1, соответствующий оптимальному набору базисных неизвестных. Проверить выполнение соотношения

H = Q^-1B
Если по оптимальной производственной программе какие-то два вида продукции не должны выпускаться, то в таблице исходных данных вычеркнуть соответствующие два столбца, составить математическую модель задачи оптимизации производственной программы с двумя оставшимися переменными, сохранив прежнюю нумерацию переменных и решить графически.

2. 
   Сформулировать задачу, двойственную линейной производственной задаче, как задачу определения расчетных оценок ресурсов, и найти ее решение, пользуясь второй основной теоремой двойственности (о дополняющей не жесткости). Указать оценку единицы каждого ресурса, минимальную суммарную оценку всех ресурсов, оценки технологий.
   

Применить найденные двойственные оценки ресурсов к решению следующей задачи.

Сформулировать задачу о "расшивке узких мест производства" и составить математическую модель. Определить область устойчивости двойственных оценок, где сохраняется структура программы производства. Решить задачу о расшивке узких мест производства при условии, что дополнительно можно получить от поставщиков не более одной трети первоначально выделенного объема ресурса любого вида (если задача окажется с двумя переменными, то только графически); найти план приобретения дополнительных объемов ресурсов, дополнительную возможную прибыль.

По пунктам 1, 2, 3 составить сводку результатов [10, c. 21].

3. 
   Составить математическую модель транспортной задачи по исходным данным из приложения 2, где вектор объемов производства А(a₁,..., a_m), потребления - В (b₁,..., b_n) и матрица транспортных издержек С=(с_ij), i = ; j = кратко записаны в виде
   

b₁ b₂ . . . b_n

a₁ c₁₁ c₁₂ . . . c_1n

a₂ c₂₁ c₂₂ . . . c_2n

. . . . . . . . . . . . . . . . . . . .

a_m c_m1 c_m2 . . . c_mn
Если полученная модель окажется открытой, то свести ее к замкнутой и найти оптимальное решение транспортной задачи методом потенциалов.

4. 
   Методом динамического программирования решить задачу распределения капитальных вложений между четырьмя предприятиями производственного объединения, располагающего суммой в 700 тыс. руб., по исходным данным, приведенным в приложении 3 (выделяемые суммы кратны 100 тыс.).
   
5. 
   Рассмотреть динамическую задачу управления производством и запасами. Решить конкретную задачу по исходным данным, приведенным в приложении 4.
   

Задача №1.
Линейная производственная задача.
На предприятии по изготовлению обуви выпускаются ботинки, тапочки, сапоги, туфли. Ресурсы, ткань, резина и кожа, выделены соответственно в количествах 150 дм², 130 дм², 124 дм². На производство ботинок идет 3 дм² ткани, 4 дм² резины, 4 дм² кожи. На производство тапочек идет 2 дм² ткани,

2 дм² резины, 3 дм² кожи. На производство сапог идет 6 дм² ткани, 3 дм² резины, 2 дм² кожи. На производство туфлей идет 5 дм² резины, 4 дм² кожи. Прибыли от реализации соответственно равны 30 млн. руб., 11 млн. руб., 45 млн. руб., 6 млн. руб.. Найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов и указать «узкие места» производства.
Решение.
Технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли имеют вид

3 2 6 0 150

А = 4 2 3 5 ; В = 130 ; С = (30, 11, 45, 6).

4 3 2 4 124
Математическая модель задачи:
Найти производственную программу

(х₁, х₂, х₃, х₄)

максимизирующую прибыль

F = 30x₁ + 11x₂ + 45x₃ + 6x₄ (1)

при ограничениях по ресурсам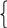

3x₁ + 2x₂ + 6x₃ ≤ 150

4x₁ + 2x₂ + 3x₃ + 5x₄ ≤ 130 (2)

4x₁ + 3x₂ + 2x₃ + 4x₄ ≤ 124

где по смыслу задачи

x₁, x₂, x₃, x₄ ≥ 0 (3)
Вводим дополнительные неотрицательные неизвестные х₅, х₆, х₇, заменяем неравенства (2) уравнениями: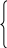




3x₁ + 2x₂ + 6x₃ + х₅ = 150

4x₁ + 2x₂ + 3x₃ + 5x₄ + х₆ = 130 (4)

4x₁ + 3x₂ + 2x₃ + 4x₄ + х₇ = 124

x₁, x₂, x₃, x₄, х₅, х₆, х₇ ≥ 0
Решаем полученную задачу симплексным методом.

Таблица 1.

Сб	Б	Н	30	11	45	6	0	0	0	α	β
			Х1	Х2	Х3	Х4	Х5	Х6	Х7
0	Х5	150	3	2	6	0	1	0	0	25	: 6
0	Х6	130	4	2	3	5	0	1	0	43 1/3	1/2
0	Х7	124	4	3	2	4	0	0	1	62	1/3
		0	-30	-11	-45	-6	0	0	0		-7 1/2
45	Х3	25	1/2	1/3	1	0	1/6	0	0	50	1/5
0	Х6	55	2 1/2	1	0	5	- 1/2	1	0	22	: 2 1/2
0	Х7	74	3	2 1/3	0	4	- 1/3	0	1	24 2/3	1 1/5
		1125	-7 1/2	4	0	-6	7 1/2	0	0		-3
45	Х3	14	0	2/15	1	-1	4/15	- 1/5	0
30	Х1	22	1	2/5	0	2	- 1/5	2/5	0
0	Х7	8	0	1 2/15	0	-2	4/15	-1 1/5	1
		1290	0	7	0	9	6	3	0

Δ_j = ‹ G_j ∙ C_б › - C_j

F_o = ‹ C_б ∙ H ›


I^’ = I : 6

II^’= II – I ∙ ½

III^’ = III – I ∙ ⅓

ΙV^’ = IV – I ∙ (- 7 ½)
I^’ = I – II ∙ 1/5

II^’= II : 2 ½

III^’ = III – II ∙ 1 1/5

ΙV^’ = IV – II ∙ (- 3)

Все Δ_j ≥ 0

Как видно из последней симплексной таблицы, оптимальная производственная программа имеет вид

Х₁ = 22, Х₂ = 0, Х₃ = 14, Х₄ = 0, (4)

а максимальная прибыль равна F_max = 1 290.

При этом первый и второй ресурсы будут исчерпаны полностью (Х₅ = 0, Х₆= 0), т. е. они образуют «узкие места» производства, а третий имеет остаток Х₇ = 8 единиц.

Обобщенный базис:




4/15 - 1/5 0

Q^-1 = - 1/5 2/5 0

4/15 - 1 1/5 1

Проверим соотношение

Н = Q^-1∙ В.




150

В = 130

124




4/15 ∙ 150 + (-1/5) ∙ 130 + 0 14

H = Q^-1_33 ∙ B_31 = (-1/5) ∙ 150 + 2/5 ∙ 130 + 0 = 22

1 2/15 ∙ 150 + (-1 1/5) ∙ 130 + 124 8
Соотношение Н = Q^-1∙ В выполняется, т. к. полученный результат совпадает с данными последней симплексной таблицы.
В оптимальной производственной программе х₂=0, х₄=0. Предположим, что вторую и четвертую продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию.

Математическая модель задачи будет выглядеть следующим образом: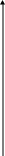

X₃

F = 30x₁ + 45x₃ → max

62

3x₁ + 6x₃ ≤ 150

4x₁ + 3x₃ ≤ 130

4x₁ + 2x₃ ≤ 124

x₁, x₃ ≥ 0

43 1/3 Grad F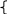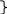



Grad F = 30, 45

50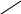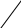

А (22, 14)








0 31 32,5 50 х₁
В точки А достигается максимальное значение функции F. Определим ее координаты и значение функции F.

3х₁ + 6х₃ = 150

4х₁ + 3х₃ = 130
х₁ = 50 – 2х₃
200 – 8х₃ + 3х₃ = 130

5х₃ = 70
х₃ = 14

х₁ = 22

F = 30 ∙ 22 + 45 ∙ 14 = 1290

F_max = 1290

Задача №2.
Двойственная задача.
Знакомый предприниматель П (Петров), занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у₁ рублей за каждую единицу первого ресурса, у₂ руб – второго, у₃ руб – третьего. Возникает вопрос: при каких ценах у₁, у₂, у₃ мы можем согласиться с предложением П.
Решение.
Определение расчетных оценок ресурсов:

найти вектор двойственных оценок

у(у₁, y₂, y₃)

минимизирующий общую оценку всех ресурсов

F = 150y₁ + 130y₂ + 124y₃ (1)

п ри условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции

3y₁ + 4y₂ + 4y₃ ≥ 30

2y₁ + 2y₂ + 3y₃ ≥ 11 (2)

6y₁ + 3y₂ + 2y₃ ≥ 45

5y₂ + 4y₃ ≥ 6

причем оценки ресурсов не могут быть отрицательными

y₁ 0, y₂ 0, y₃ 0. (3)

Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений (х₁, х₂, х₃, х₄) и (y₁, y₂, y₃) пары двойственных задач необходимо и достаточно выполнение условий




Х₁(3y₁ + 4y₂ + 4y₃ – 30) = 0 у₁(3x₁ + 2x₂ + 6x₃ - 150 ) = 0

Х₂(2y₁ + 2y₂ + 3y₃ – 11) = 0 ; у₂(4x₁ + 2x₂ + 3x₃ + 5x₄ – 130) = 0 .

Х₃(6y₁ + 3y₂ + 2y₃ – 45) = 0 у₃(4x₁ + 3x₂ + 2x₃ + 4x₄ – 124) = 0

Х₄( 5y₂ + 4y₃ – 6) = 0
Ранее было найдено, что в решении исходной задачи х₁>0, x₃>0. Поэтому




3y₁ + 4y₂ + 4y₃ – 30 = 0

6y₁ + 3y₂ + 2y₃ – 45 = 0
Если же учесть, что третий ресурс был избыточным и, согласно той же теореме двойственности, ее двойственная оценка равна нулю

У₃=0,

т о приходим к системе уравнений

3y₁ + 4y₂ – 30 = 0

6y₁ + 3y₂ – 45 = 0

у₂ = 15 - 2у₁

3у₁ + 4∙ (15 - 2у₁) = 30

3у₁ + 60 – 8у₁ = 30

5у₁ = 30

откуда следует

у₁=6, у₂=3.

Таким образом, получили двойственные оценки ресурсов
у₁=6; у₂=3; у₃=0, (4)
причем общая оценка всех ресурсов равна 1 290.

Решение (4) содержится в последней строке последней симплексной таблицы исходной задачи.

Экономический смысл двойственных оценок:

• 
  двойственная оценка первого ресурса у₁=6 показывает, что добавление одной единицы первого ресурса обеспечит прирост прибыли в 6 единиц;
  
• 
  двойственная оценка второго ресурса у₂=3 показывает, что добавление одной единицы второго ресурса обеспечит прирост прибыли в 3 единицы;
  
• 
  оценка второй технологии Δ₂ = 7 показывает, что если произвести одну единицу продукции второго вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 7 единиц;
  
• 
  оценка четвертой технологии Δ₄ = 9 показывает, что если произвести одну единицу продукции четвертого вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 9 единиц.
  

Задача о "расшивке узких мест производства".
При выполнении оптимальной производственной программы первый и второй ресурсы используются полностью, т.е. образуют узкие места производства. Будем их заказывать дополнительно. Пусть T(t₁,t₂,t₃)- вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие

H + Q^-1T 0.

Задача состоит в том, чтобы найти вектор

T (t₁, t₂, 0),

максимизирующий суммарный прирост прибыли

W = 6t₁ + 3t₂ (1)

при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)
14 4/15 -1/5 0 t₁ 0

22 + -1/5 2/5 0 ∙ t₂ ≥ 0 (2)

8 4/15 -1 1/5 1 0 0
предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида



t₁ 150

t₂ ≤ 1/3 ∙ 130 (3)

0 124

причем по смыслу задачи

t₁ 0, t₂ 0. (4)

Переписав неравенства (2) и (3) в виде


4/15t₁ - 1/5t₂ ≥ -14

-1/5t₁ + 2/5t₂ ≥ -22 (5)

4/15t₁ - 1 1/5t₂ ≥ -8

t₁≤ 50

t₂≤ 43 1/3

п риходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).

t₂

70












-52,5 -30 6 2/3




110 t₁



-55








Область устойчивости двойственных оценок.





Grad W = 6, 3

t₂


43 1/3

A (50, 17 7/9)






6 2/3



0 50 t₁



t₁ = 50 t₁ = 50

4/15 t₁ –1 1/5 t₂ = -8 t₂ = 17 7/9

W = 6 ∙ 50 + 3 ∙17 7/9 = 353 1/3

Отсюда следует, что программа расшивки имеет вид

t₁= 50 , t₂= 17 7/9 , t₃=0
и
прирост прибыли составит 353 1/3.
F^H_max = 1290 + 353 1/3 = 1643 1/3
X₃^н = 14 + 4/15 ∙ 50 – 1/5 ∙ 17 7/9 = 23 7/9

Х₁^н = 22 – 1/5 ∙ 50 + 2/5 ∙ 17 7/9 = 19 1/9

X₇^н = 8 + 4/15 ∙ 50 – 1 1/5 ∙ 17 7/9 = 0
F^H_max = 45 ∙ 23 7/9 + 30 ∙ 19 1/9 = 1643 1/3

Сводная таблица результатов по задачам №1 и №2.

Таблица 2.

сj	30	11	45	6	B	x4+i	yi	ti
	3	2	6	0	150	0	6	50
aij	4	2	3	5	130	0	3	17 7/9
	4	3	2	4	124	8	0	0
xj	22	0	14	0	1290			353 1/3
j	0	7	0	9

Задача №3.
Транспортная задача.

Однородный продукт, сосредоточенный в 3пунктах производства (хранения) в количествах 50, 70, 30 единиц, необходимо распределить между 4 пунктами потребления, которым необходимо соответственно 30, 11, 45, 36 единиц. Стоимости перевозок единицы продукта из пункта отправления в пункт назначения равны

3 2 6 7

С = 7 8 3 5

4 3 4 6

Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были минимальными.
Решение.
Д

ля решения транспортной задачи применяем метод потенциалов.

Исходные данные задачи имеют вид

3 2 6 7

А(а₁, а₂, а₃) = (50; 70; 30); В(b₁, b₂, b₃, b₄) = (30; 11; 45; 36); С = 7 8 3 5

4 3 4 6

Общий объем производства а_i = 50 + 70 + 30 = 150 больше, требуется всем потребителям b_i = 30 + 11 + 45 + 36 = 122, т.е. имеем открытую модель транспортной задачи. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления 150-122 = 28 единиц, причем тарифы на перевозку в этот пункт условимся считать равными нулю, помня, что переменные, добавляемые к левым частям неравенств для превращения их в уравнения, входят в функцию цели с нулевыми коэффициентами.

Первое базисное допустимое решение легко построить по правилу северо-западного угла.

Таблица 3.

Потребление Производство	b1 = 30	b2 = 11	b3 = 45	b4 = 36	b5 = 28
a1 = 50	30 3	11 2	9 6	7	0 *	u1 = 0
a2 = 70	7	8	36 3	34 5	0	u2 = - 3
a3 = 30	4	3	4	2 6	28 0	u3 = - 2
	v1 = 3	v2 = 2	v3 = 6	v4 = 8	v5 = 2

Один из потенциалов выбираем произвольно, так как одно уравнение линейно зависит от остальных. Положим, что u₁ = 0. Остальные потенциалы находим из условия, что для базисных клеток . В данном случае получаем
₁₁ = 0, u₁ + v₁ - c₁₁ = 0, 0+ v₁ -3 = 0, v₁ = 3

₁₂ = 0, u₁ + v₂ - c₁₂ = 0, 0+ v₂ -2 = 0, v₂ = 2

₁₃ = 0, u₁ + v₃ – c₁₃ = 0, 0 + v₃ -6 = 0, v₃ = 6

₂₃ = 0, u₂ + v₃ – c₂₃ = 0, u₂ + 6 – 3 = 0, u₂ = - 3

₂₄ = 0, u₂ + v₄ – c₂₄ = 0, - 3 + v₄ – 5 = 0, v₄ = 8

₃₄ = 0, u₃ + v₄ – c₃₄ = 0, u₃ + 8 – 6 = 0, u₃ = - 2

₃₅ = 0, u₃ + v₅ – c₃₅ = 0, - 2 + v₅ – 0 = 0, v₅ = 2.

Затем вычисляем оценки всех свободных клеток:

₂₁ = u₂ + v₁ - c₂₁ = - 3 + 3 - 7 = - 7

₃₁ = u₃ + v₁ - c₃₁ = - 2 + 3 - 4 = - 3

₂₂ = u₂ + v₂ - c₂₂ = - 3 + 2 – 8 = - 9

₃₂ = u₃ + v₂ – c₃₂ = - 2 + 2 – 3 = - 3

₃₃ = u₃ + v₃ – c₃₃ = - 2 + 6 – 4 = 0

₁₄ = u₁ + v₄ – c₁₄ = 0 + 8 – 7 = 1

₁₅ = u₁ + v₅ – c₁₅ = 0 + 2 – 0 = 2

₂₅ = u₂ + v₅ – c₂₅ = - 3 + 2 – 0 = -1.

Находим наибольшую положительную оценку

max ( ) = 2 = ₁₅

Для найденной свободной клетки 15 строим цикл пересчета - замкнутую ломаную линию, соседние звенья которой взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке, а все остальные - в занятых клетках. Это будет 15 – 13 – 23 – 24 – 34 - 35. Производим перераспределение поставок вдоль цикла пересчета

Таблица 4.

9				9 - α		+α				9
36	34			36 + α	34 - α			45	25
	2	28			2 + α	28 - α			11	19

= 9

Получаем второе базисное допустимое решение:

Таблица 5.

Потребление Производство	b1 = 30	b2 = 11	b3 = 45	b4 = 36	b5 = 28
a1 = 50	30 3	11 2	6	7	9 0	u1 = 0
a2 = 70	7	8	45 3	25 5	0	u2 = - 1
a3 = 30	4	3	4	11 6	19 0	u3 = 0
	v1 = 3	v2 = 2	v3 = 4	v4 = 6	v5 = 0

Находим новые потенциалы. Положим, что u₁ = 0. Остальные потенциалы находим из условия, что для базисных клеток . В данном случае получаем:
₁₁ = 0, u₁ + v₁ - c₁₁ = 0, 0 + v₁ - 3 = 0, v₁ = 3

₁₂ = 0, u₁ + v₂ - c₁₂ = 0, 0 + v₂ - 2 = 0, v₂ = 2

₁₅ = 0, u₁ + v₅ – c₁₅ = 0, 0 + v₅ – 0 = 0, v₅ = 0

₃₅ = 0, u₃ + v₅ – c₃₅ = 0, u₃ + 0 – 0 = 0, u₃ = 0

₃₄ = 0, u₃ + v₄ – c₃₄ = 0, 0 + v₄ – 6 = 0, v₄ = 6

₂₄ = 0, u₂ + v₄ – c₂₄ = 0, u₂ + 6 – 5 = 0, u₂ = - 1

₂₃ = 0, u₂ + v₃ – c₂₃ = 0, - 1 + v₃ – 3 = 0, v₃ = 4.


Вычисляем оценки всех свободных клеток:

₂₁ = u₂ + v₁ - c₂₁ = - 1 + 3 - 7 = - 5

₃₁ = u₃ + v₁ - c₃₁ = 0 + 3 - 4 = - 1

₂₂ = u₂ + v₂ - c₂₂ = - 1 + 2 – 8 = - 7

₃₂ = u₃ + v₂ – c₃₂ = 0 + 2 – 3 = - 1

₁₃ = u₁ + v₃ – c₁₃ = 0 + 4 – 6 = - 2

₃₃ = u₃ + v₃ – c₃₃ = 0 + 4 – 4 = 0

₁₄ = u₁ + v₄ – c₁₄ = 0 + 6 – 7 = - 1

₂₅ = u₂ + v₅ – c₂₅ = - 1 + 0 – 0 = -1.
Все оценки свободных клеток _ij ≤ 0, следовательно, мы получили оптимальное базисное допустимое решение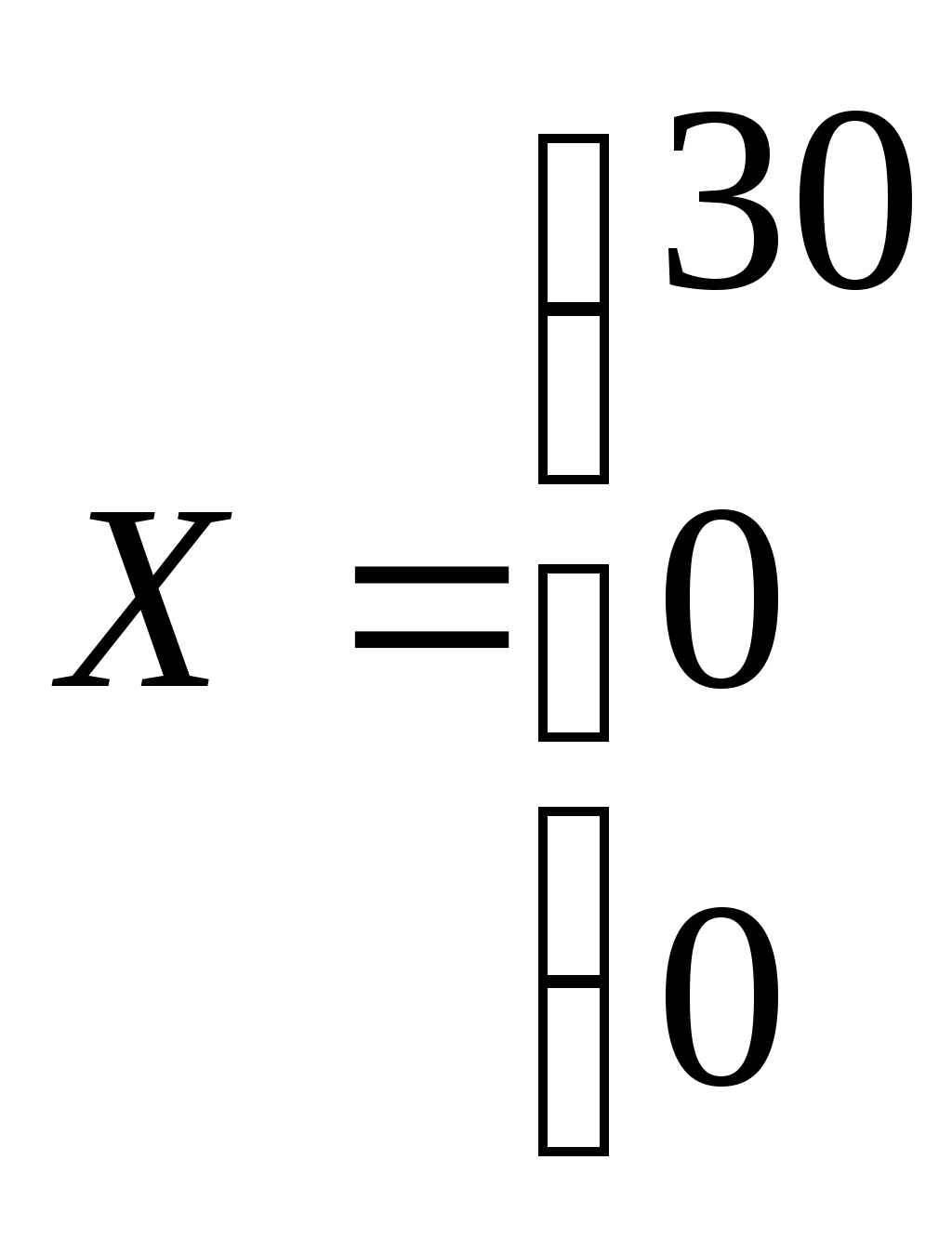



Определяем минимальные транспортные расходы по доставке продуктов.

F = 30 ∙ 3 + 11 ∙ 2 + 45 ∙ 3 + 25 ∙ 5 + 11 ∙ 6 = 438 ед.
В первом базисном решении эти расходы составляли 456 ед.

F₁ = 30 ∙ 3 + 11 ∙ 2 + 9 ∙ 6 + 36 ∙ 3 + 34 ∙ 5 + 2 ∙ 6 = 456


Задача № 4.
Динамическое программирование.
Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций f_j(x_j) приведены в таблице 6, где, например, число 76 означает, что если третье предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 76 тыс. руб.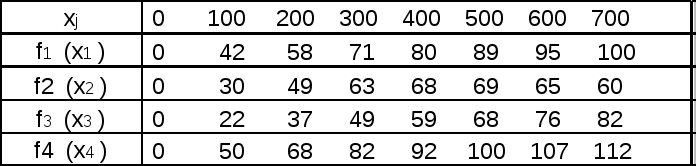

Таблица 6.



Решение.
Прежде всего заполняем табл. 7. Значения f₂(x₂) складываем со значениями F₁( - x₂) = f₁(- x₂) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение . Заполняем таблицу 8.

Продолжая процесс, табулируем функции F₃(), () и т.д. В табл. 11 заполняем только одну диагональ для значения = 700. Наибольшее число на этой диагонали:

Z_max = 197 тыс. руб.,

причем четвертому предприятию должно быть выделено

х^*₄ = ₄ (700) = 200 тыс. руб.

На долю остальных трех предприятий остается 500 тыс. руб. Из табл. 10 видно, что третьему предприятию должно быть выделено

x^*₃ = ₃ (700-x^*₄) = ₃ (500) = 100 тыс. руб.

Продолжая обратный процесс, находим

x*₂ = ₂ (700 - x*₄ - x*₃) = ₂ (400) = 200 тыс. руб.

На долю первого предприятия остается

x*₁ = 700 - x*₄ - x*₃ - x*₂ = 200 тыс. руб.

Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:

x*₁ =200; x*₂ =200; x*₃ = 100; x*₄ = 200.

Оно обеспечивает производственному объединению наибольший воможный прирост прибыли 197 тыс. руб.