морфология культуры. Задачи1 - теплопроводность (5-14). Задача 1 Определить величину теплового потока
 Скачать 42.67 Kb. Скачать 42.67 Kb.
|
|
Задача 1 Определить величину теплового потока Q, количество тепла QΣ, передаваемого через стенку печи толщиной δ, м, за время t, ч, если коэффициент теплопроводности материала равен λ, Вт/(м·К), а поверхность стенки F,м2, и температуры внешних поверхностей стенки равны Т П1и Т П2, °С. Исходные данные:
Решение: 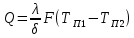 = =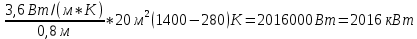 2016 кВт = 2016 кДж/с QΣ = Q*t = 2016к Дж/с * 0,5ч = 2016*4,0*3600=29030400кДж = 29,03 МДж. Ответ: Q = 2016 кВт, QΣ = 29,03 МДж. Задача 2 Через стенку печи размером 2х3, м, коэффициент теплопроводности которой равен 0,5Вт/(м·К), проходит тепловой поток 1500Вт. Какова должна быть толщина стенки, чтобы температура второй поверхности ТП2 была ниже заданной температуры 780°С, первой поверхности в 0,5раз? Исходные данные:
Решение:   3 Задача Определить температуру внутри стенки толщиной δ, м, на расстоянии х,м, от левой поверхности, имеющий температуру, ТП1,°'С, если коэффициент теплопроводности стенки при нормальных условиях равен λ0, Вт/(м·К), а температура правой поверхности равна ТП2,°С. Исходные данные:
Решение: Пусть Tв – температура внутри стенки. Иходя из уравнения с двумя неизвестными получаем: TП1=xA+b=1280; Tв=0,1A+b=0,1A+1280; TП2=0,13A+b=0,13A+1280 Из 3 уравнения следует: A= 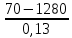 = -9307,7 = -9307,7Подставляя А во 2 уравнения получаем: Тв=0,1*(-9307,7)+1280=349,23град. Ответ: 349,23град. Задача 4. Определить плотность теплового потока через стенку толщиной δ, м, имеющую коэффициент теплопроводности λ, Вт/(м·К), и температуру на внешних поверхностях ТП1 и ТП2, °С. Как изменится величина плотности теплового потока, если без изменения суммарной толщины и температур внешних поверхностей однослойная стенка заменена на двуслойную с толщинами слоев δ1 и δ2, м, и коэффициентами теплопроводности λ1 и λ2? Считать, что коэффициенты теплопроводности не зависит от температуры (табл. 4). Исходные данные:
Решение:  = =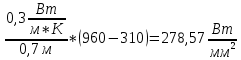 Для двухслойной пластины: 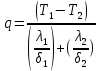 = = 278,57-26,6= 251,97 Вт/ 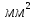 – на столько уменьшилась плотность теплового потока с двуслойной стенкой. – на столько уменьшилась плотность теплового потока с двуслойной стенкой.Ответ: q1= 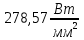 q2= q2=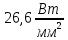 . .Задача 5 Определить разность температур на внешних поверхностях однослойной стенки толщиной δ, м, если коэффициент теплопроводности материала равен λ, Вт/(м·К), а плотность теплового потока равна q, Вт/м2 (табл. 5). Исходные данные:
Решение: Согласно уравнению q= 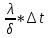 , => , => 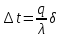 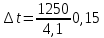 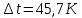 Ответ: 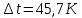 Задача 6 Трехслойная кладка печи, состоящая из слоев толщиной δ1, δ2, δ3, м, с коэффициентами теплопроводности соответственно λ1, λ2, λ3, Вт/(м·К), заменяется двуслойной с удалением среднего слоя. Определить необходимую толщину внешнего слоя при условии неизменности величины тепловых потерь через стенку (табл. 6). Исходные данные:
Решение: Для 3х слойной кладки печи: Q = 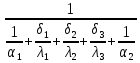 (Tж1-Tж2) (Tж1-Tж2)Для 2х слойной кладки печи: Q = 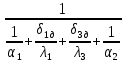 (Tж1-Tж2) (Tж1-Tж2)Соответственно, чтобы тепловой поток не изменился, 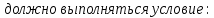  = =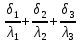 При условии, что слои будут равны, получаем: 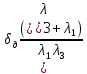 = =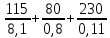 = 2205 = 2205δд = 2205*  = 2205*8,1*0,11/(8,1+0,11)=239,3мм = 2205*8,1*0,11/(8,1+0,11)=239,3ммОтвет: δд = 239,3 мм. Задача 7 Определить коэффициент теплопередачи k, температуры внешних поверхностей и плотность теплового потока q через однослойную стенку печи толщиной δ, м, имеющую коэффициент теплопроводности λ, Вт/(м·К), если температура газов в печи равна Тж1|, °С, а температура окружающего воздуха равна Тж2, °С; коэффициенты теплоотдачи равны соответственно α1и α2, Вт/(м2·К), (табл). Исходные данные:
1)Коэффициент теплопередачи Q=K*(T1-T2) 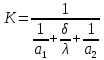 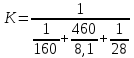 =0,0176 =0,0176Q=0,0176*(1200-35)=20,5 Вт/м*С⁰ 2)Температура внешних поверхностей 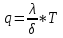 20,5=  *T *TT=11,64 3)Плотность теплового потока 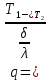 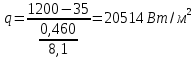 Задача 8 Определить разность температур внешних поверхностей однослойной стенки печи и градиент температуры в стенке толщиной δ, м, с коэффициентом теплопроводности λ, Вт/(м·К), разделяющей дымовые газы и окружающий воздух с температурами Тж1 и Тж2 , °С, если коэффициенты теплоотдачи равны соответственно α1 и α2, Вт/(м2·К) (табл. 8). Исходные данные:
Решение: Q = 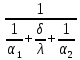 (Tж1-Tж2) = (Tж1-Tж2) =  (1280-20) = 1275,67 Вт/м2; (1280-20) = 1275,67 Вт/м2;Q=α*(Tж – Tc1); Tc1 = 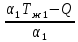 ; ; Tc1 = 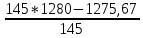 =1271,2 К; =1271,2 К;Q=α*(Tс2 – Tж); Tс2 =  ; ; Tс2 = 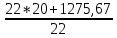 =77,985К; =77,985К;∆T = 1271,2 – 77,985 = 1193,215 Градиент температуры(обозначается gradT или T) – вектор, направленный по нормали к изотермической поверхности, в сторону увеличения температуры и численно равный изменению температуры на единице длины: T = ∆T/ δ = 1193,215/200=5,97 мм-1 Задача 9 Дымовые газы печи и окружающий воздух с температурами Тж1 и Тж2,°С разделены стенкой толщиной δ,м, коэффициент теплопроводности которой, равен λ, Вт/(м·К). Как изменится плотность теплового потока и температуры внешних поверхностей стенки, если стенка такой же толщины будет состоять из двух слоев δ1и δ2, м, с коэффициентами теплопроводности соответственно λ1 и λ2, Вт/(м·К)? Коэффициенты теплоотдачи равны α1 = 120 Вт/(м2·К), α2=22Вт/(м2·К) (табл. 9). Исходные данные:
Решение: Для однослойной стенки: Q = 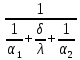 (Tж1-Tж2)= (Tж1-Tж2)=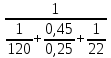 (1600-20)=1580,5 Вт/м2 (1600-20)=1580,5 Вт/м2Для многослойной стенки: Q = 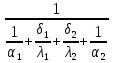 (Tж1-Tж2)= = (Tж1-Tж2)= = 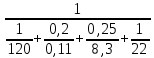 (1600-20)=830,7 Вт/м2 (1600-20)=830,7 Вт/м2Разница: ∆Q=1580,5-830,7 = 749,8 Вт/м2 Рассчитаем температуры поверхностей стенок для однослойной: Q1=α*(Tж – Tc); Tc = 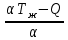 ; ; Q2=α*(Tс – Tж); Tс = 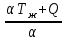 ; ; Tc1о = 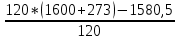 =1859,8K. =1859,8K.Tc2о =  =364,8К. =364,8К.Температуры поверхностей для многослойной: Tc1м = 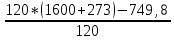 =280,08K. =280,08K.Tc2м =  =317,08К. =317,08К.Разница температур поверхностей: ∆Tc1 = 1859,8 – 280,08 = 1579,72 (повысилась) ∆Tc2 = 364,8 – 317,08 = 47,72 (понизилась) Задача 10 Футеровка печи состоит из трех слоев с толщинами δ1, δ2 и δ3, м, коэффициенты теплопроводности которых соответственно равны λ1, λ2, λ3, Вт/(м·К). Температура газов внутри печи Тж1, окружающего воздуха Тж2, °С. Определить плотность теплового потока через стенку, температуру на внешних поверхностях стенки и на границе раздела слоев, если коэффициенты теплоотдачи равны α1 и α2, Вт/(м2·К) (табл. 10). Исходные данные:
Плотность теплового потока q определяется так: 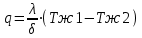 Для трехслойной стенки плотность теплового потока определяется так: 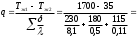 1,16 1,16Температуры на контактирующих поверхностях будут равны:  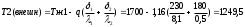 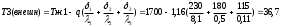 |
