Тех.мех. Задача С1 Жесткая рама (рис. 0 9, табл. С1) закреплена в точке а шарнирно, а в точке
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
СТАТИКА Задача С1 Жесткая рама (рис. С1. 0—С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р=25 кН. На раму действует пара сил с моментом М=60 кН-м и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действуют сила F2под углом 15° к горизонтальной оси, приложенная в точке D, и сила F3 под углом 60° к горизонтальной оси, приложенная в точке Е и т.д.).Определить реакции связей в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах принять а=0,5 м.   Дано: P=25 кН, М=60 кНм, F2= 20 кН, F3= 30 кН, а= 0,5 м. Найти: Реакции связей в т. А и В Решение  Рассмотрим равновесие жесткой рамы. На раму действуют силы: силы  и и  , пара сил с моментом М, натяжение троса , пара сил с моментом М, натяжение троса  ( ( ) и реакции связей ) и реакции связей  , ,  , ,  . .Неизвестны реакции связей  , ,  , ,  . .Для полученной плоской системы сил составим три уравнения равновесия:  , ,  (1) (1) , ,  (2) (2) , ,  (3) (3)Из уравнения (3):   41,66 кН 41,66 кНИз уравнения (2):  -63,4 кН -63,4 кНИз уравнения (1):  15,15 кН 15,15 кНРеакции, полученные со знаком «минус», в действительности имеют направление противоположное принятому на рисунке. Проверка:     Ответ: ХА = 15,15 кН, YA = -63,4 кH, RB = 41,66 кH Задача С2 Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно (рис.С2.0-С2.5),или свободно опираются друг о друга (рис С2.6-С2.9).Внешними связями,наложенными на конструкцию, являются в точке А или шарнир, или жесткая заделка; в точке В или невесомый стержень ВВ(рис.0 и1),или гладкая плоскость (рис.2 и 3),или шарнир (рис.4-9); в точке D или невесомый стержень DD (рис.1,2,7), или шарнирная опора на катках (рис. 9). На каждую конструкцию действуют: пара сил с моментом М — = 60 кН·м, равномерно распределенная нагрузка интенсивности q= =20 кН/м и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С2; там же в столбце «Участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила F2под углом 60° к горизонтальной оси, приложенная в точке L, сила F4 под углом 30° к горизонтальной оси, приложенная в точке Е, и нагрузка, распределенная на участке СК. Определить реакции связей в точках А, В, С (для рис. 1,2,7,9, еще и в точке D), вызванные заданными нагрузками. При окончательных расчетах принять а=0,2 м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С2а.   Дано: М=60 кНм, q=20 кН/м, а=0,2 м,  =20 кН, =20 кН,  =40 кН =40 кННайти: Найти реакции связей в т. А, В,С. Решение  Для определения реакций расчленим систему и рассмотрим вначале равновесие стержня ВС. На стержень действуют сила  , пара сил с моментом М, реакция , пара сил с моментом М, реакция  и составляющие и составляющие  , ,  реакции опоры В. реакции опоры В.Для полученной плоской системы сил составляем уравнения равновесия:  ; ;  (1) (1) ; ;  (2) (2) ; ;  (3) (3)Из (3):  = = (кН) (кН)Из (2):  = = (кН) (кН) Из (1):  = = (кН) (кН)Теперь рассмотрим равновесие угольника АЕL. На него действует сила  , равномерно распределенная нагрузка, которую заменим силой , равномерно распределенная нагрузка, которую заменим силой 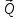 , приложенной в середине участка , приложенной в середине участка  ( ( =20 кН), сила давления стержня ВС =20 кН), сила давления стержня ВС  (направлена противоположно (направлена противоположно  и численно и численно  ) и реакция жесткой заделки А ( ) и реакция жесткой заделки А ( , ,  , ,  ). ).Для этой плоской системы сил тоже составим уравнения равновесия:  ; ;  (4) (4) ; ;  (5) (5) ; ;  (6) (6)Из (4):  = = (кН) (кН) Из (5):  = = (кН) (кН)Из (6):  (кНм) (кНм) Реакции, полученные со знаком «минус» в действительности имеют направление противоположное принятому на рисунке. Проверка (для всей конструкции):         Ответ:
КИНЕМАТИКА Задача К2 Механизм состоит из ступенчатых колес 1—3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2.0—К2.9, табл. К2). Радиусы ступеней колес равны соот-ветственно: у колеса 1-r1=2 см, R1=4 см, у колеса 2-r2=6 см, R2=8 см, у колеса 3-r3=12 см, R3=16 см. На ободьях колес расположены точки А, В,С. В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где φ1(t)— закон вращения колеса 1, S4(t)—закон движения рейки 4, ω2(t)—закон изменения угловой скорости колеса 2, V5(t) - закон изменения скорости груза 5и т. д. (везде φ выражено в радианах, s — в сантиметрах, t — в секундах). Положительное направление для φ и ω) против хода часовой стрелки, для S4, S5и V4, V5 — вниз. Определить в момент времени t1=2 с указанные в таблице в столбцах «Найти» скорости (v— линейные, со ω —угловые) и ускорения (a — линейные, ε — угловые) соответствующих точек или тел (V5 — скорость груза 5 и т. д.).   Дано: r1= 2 см, R1= 4 см, r2= 6 см, R2= 8 см, r3= 12 см, R3= 16 см,  , t1=2 c. , t1=2 c.Найти: скорости  , ,  , ускорения , ускорения  , ,  , , 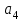 . .Решение С  корости точек, лежащих на ободах колес радиуса корости точек, лежащих на ободах колес радиуса  , обозначим через , обозначим через  , а точек, лежащих на ободах колес радиуса , а точек, лежащих на ободах колес радиуса  , через , через  . .Угловые скорости всех колес. Колеса 3 и 2 находятся в зацеплении, следовательно,  , то есть , то есть  и отсюда и отсюда  . . При t1=2 c  =1 (1/с). =1 (1/с).Скорость  Т.к. колеса 2 и 1 связаны ременной передачей, то  или или  и и  . . . . При t1=2 c  =6 (см/с) =6 (см/с)Угловое ускорение  . . Так как  , то , то  = = = –5 (1/с2). = –5 (1/с2).Ускорение  . . Для т.А  , где , где  , ,  . . Угловое ускорение  = = = = = –7,5 (1/с2). = –7,5 (1/с2). Таким образом при t1=2 c касательная составляющая  (см/с2), (см/с2), нормальная составляющая  = = = 18 (см/с2), = 18 (см/с2),полное ускорение  = = = 23,4 (см/с2). = 23,4 (см/с2). | ||||||||||||||||||
