теория вероятности. Задача Суточное потребление электроэнергии на рабочем месте в цехе может быть рассмотрено как случайная величина
 Скачать 181 Kb.
|
|
Задача Суточное потребление электроэнергии на рабочем месте в цехе может быть рассмотрено как случайная величина Х, распределенная по нормальному закону. Было произведено 40 измерений этой величины (табл. 5.1). 1.1 Провести группировку данных, разбив варианты на 5 интервалов. 1.2 Для сгруппированного ряда построить гистограмму частот. 2.1 Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х. 2.2 Построить доверительный интервал для генеральной средней и генераль-ного среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95. 3.1 При уровне значимости α = 0,05 проверить утверждение энергослужб предприятия, что среднесуточное потребление электроэнергии на рабочем месте равно a (табл. 5.2). 3.2 После переналадки оборудования, произведенной с целью уменьшения потребления электроэнергии, были проведены новые измерения, и получена выборка объема 10 (табл. 5.3.). При уровне значимости α проверить, является ли статистически обоснованным утверждение производителя об уменьшении среднего потребления электроэнергии.
1.1 Проведем группировку исходных данных, т.е. разобьем варианты на отдельные интервалы. Найдем разность между наибольшим и наименьшим значениями признака: xmax – xmin = 5,09 – 2,98 =2,11. Тогда при разбивке на 5 интервалов длина интервала составит h = 2,11/5=0,422  (округляем всегда с избытком). Для упрощения дальнейших расчетов выберем границы интервалов таким образом, чтобы середины интервалов являлись как можно более «круглыми» числами (с наименьшим числом знаков после запятой). Получим табл. 1. Таблица 1
1.2 Построим для сгруппированного ряда гистограмму частот. 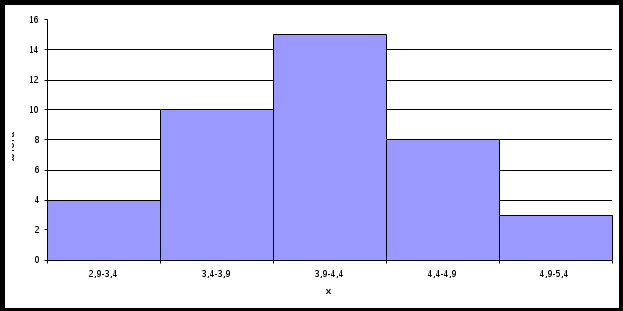 Рис.1. Гистограмма 2.1 Найдем выборочную среднюю по формуле:   Найдем выборочную дисперсию Dв по формуле  Найдем исправленную выборочную дисперсию по формуле Найдем исправленное выборочное среднеквадратическое отклонение случайной величины Х  2.2 Построим доверительный интервал для генеральной средней с уровнем доверительной вероятности γ = 0,95. Так как значение генеральной дисперсии неизвестно, пользуемся формулой  . Найдем значение  Далее находим точность оценки  доверительный интервал для генеральной средней имеет вид  Подставляя значения, получаем, что с вероятностью 0,95 выполнено  Построим доверительный интервал для генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95. Найдем значение χ1,2 по таблице критических точек распределения χ2 при уровне вероятности (1 + γ) / 2 = 0,975 и числе степеней свободы k = n – 1 = 39. Получаем 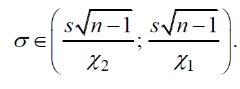 , следовательно,  . Найдем значение  по таблице критических точек распределения при уровне вероятности (1 – γ) / 2 = 0,025 и числе степеней свободы k = n – 1 = 39. Получаем  , следовательно,  . Доверительный интервал для генерального среднеквадратического отклонения имеет вид   3.1 При уровне значимости α = 0,05 проверим утверждение, что среднее значение величины Х соответствует проектному значению a = 4. Так как выборка имеет большой объем (n = 40 > 30), то для проверки нулевой гипотезы Н0: в качестве критерия проверки можно принять случайную величину U, определенную по формуле  При этом в качестве генерального среднеквадратического отклонения σ можно принять выборочное значение s. Вычислим наблюдаемое значение критерия  Конкурирующей является гипотеза  : , поэтому критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – α)/2 = 0,475. Получаем Uкр=1,96. Так как |Uнабл| < Uкр, то нет оснований отвергнуть нулевую гипотезу. Следовательно, утверждение, что среднее значение входного параметра Х соответствует проектному значению, является статистически обоснованным. 3.2 Для первой выборки объема  = 40 были получены значения  ;  . Найдем выборочную среднюю и выборочное среднеквадратическое отклонение для второй выборки объема  = 10 (табл 5.3).
Так как все варианты встречаются в выборке по одному разу, для нахождения выборочной средней пользуемся формулой 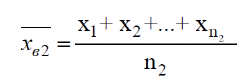 Получаем  Для нахождения выборочной дисперсии воспользуемся формулой: 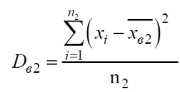 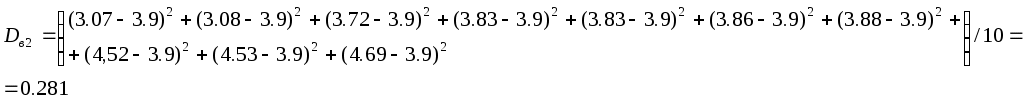 Найдем исправленную выборочную дисперсию: Найдем исправленное выборочное среднеквадратическое отклонение случайной величины Х  Проверяем теперь гипотезу о равенстве двух генеральных средних, т.е. гипотезу H0:  . Предполагаем, что дисперсии двух выборок равны.Поскольку мы проверяем утверждение, что среднее значение выходного параметра увеличилось, то в качестве конкурирующей выбираем гипотезу 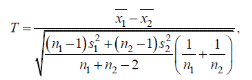 :  . Так как генеральные дисперсии неизвестны, а объем одной из выборок мал, используем критерий.  Наблюдаемое значение критерия  Критическую точку Tкр (2α; n1 + n2 – 2) = Tкр(0,1; 48) = 1,67 правосторонней критической области находим по таблице критических точек распределения Стьюдента при n1 + n2 – 2 степенях свободы и верности 2α. Так как  , то нет оснований отвергнуть нулевую гипотезу., т.е. утверждение об уменьшении среднего значения показателя Х неявляется статистически обоснованным. |
