Главная страница
Навигация по странице:

  • Рис. 2

    		•

    вариант 13. Вариант 13. Задание. Имеются данные о стаже работы сотрудников предприятия, лет. По имеющимся данным требуется Построить статистический ряд распределения, изобразить получившийся ряд графически с помощью полигона или гистограммы.


    Скачать 83.94 Kb.
    НазваниеЗадание. Имеются данные о стаже работы сотрудников предприятия, лет. По имеющимся данным требуется Построить статистический ряд распределения, изобразить получившийся ряд графически с помощью полигона или гистограммы.
    Анкорвариант 13
    Дата18.05.2023
    Размер83.94 Kb.
    Формат файлаdocx
    Имя файлаВариант 13.docx
    ТипДокументы
    #1140504

    Задание. Имеются данные о стаже работы сотрудников предприятия, лет.



    По имеющимся данным требуется:

    1. Построить статистический ряд распределения, изобразить получившийся ряд графически с помощью полигона или гистограммы. Найти функцию распределения, построить её график.

    2. Найти выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение выборки.

    3. Выдвинуть гипотезу о виде распределения генеральной совокупности.

    Решение.

    1. Для полученной выборочной совокупности объёмом n  40:

    а) Производим ранжирование выборочных данных, располагая их в порядке возрастания:

    1
    2
    3
    3
    4
    5
    6
    6
    7
    8

    8
    9
    9
    9
    10
    10
    10
    11
    11
    11

    11
    12
    12
    12
    12
    12
    14
    15
    15
    15

    16
    17
    17
    18
    18
    19
    19
    20
    21
    26

    б) Определяем минимальное и максимальное значение признака: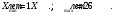



    в) Находим размах варьирования признака: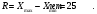



    г) Определяем число групп, на которые разбиваем выборочную совокупность (округление проводим до ближайшего целого)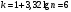



    д) Определяем длину интервала по формуле: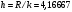



    е) Определяем границы интервалов и группируем данные по соответствующим интервалам. Границы интервалов ai, bi , i 1, 2, ..., k, получаем следующим образом: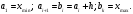



    № интервала
    Границы интервала ai -bi
    Частота mi
    Накопленная частота mΣi

    0
    1
    2
    3

    1
    1 - 5,166666667
    6
    6

    2
    5,166667 - 9,333333333
    8
    14

    3
    9,333333 - 13,5
    12
    26

    4
    13,5 - 17,66666667
    7
    33

    5
    17,66667 - 21,83333333
    6
    39

    k=6
    21,83333 - 26
    1
    40

    Σ
    -
    40
    -

    ж) На основе полученных данных строим статистический ряд распределения и его геометрические представления. В пределах каждого интервала все значения признака приравниваем к его серединному значению (ai + bi)/2 и считаем, что частота относится именно к этому значению. Необходимые вычисления производим в таблице:

    № интервала
    Границы интервала ai -bi
    xi=(ai+bi)/2
    Частости wi=mi/n
    Накопленные частости wΣi=mΣi/n
    Относит. плотность распределения wi/h

    0
    1
    2
    3
    4
    5

    1
    1 - 5,166666667
    3,083333333
    0,15
    0,15
    0,036

    2
    5,166667 - 9,333333333
    7,25
    0,2
    0,35
    0,048

    3
    9,333333 - 13,5
    11,41666667
    0,3
    0,65
    0,072

    4
    13,5 - 17,66666667
    15,58333333
    0,175
    0,825
    0,042

    5
    17,66667 - 21,83333333
    19,75
    0,15
    0,975
    0,036

    k=6
    21,83333 - 26
    23,91666667
    0,025
    1
    0,006

    Σ
    -
    -
    1
    -
    -

    Статистический ряд распределения образуют данные 2-го и 3-го столбцов таблицы. Для построения гистограммы распределения используются данные 1- го и 5-го столбцов, полигона – 2-го и 5-го столбцов, кумуляты (функции распределения) – данные 1-го и 4-го столбцов. Напомним, что для построения гистограммы по оси абсцисс откладываются частичные интервалы ai, bi  , на каждом из которых строим прямоугольник высотой wi/h. Площадь ступенчатой фигуры, образуемой гистограммой, равна единице. Соединяя середины верхних оснований прямоугольников отрезками прямой, из гистограммы можно получить полигон распределения (рис. 1).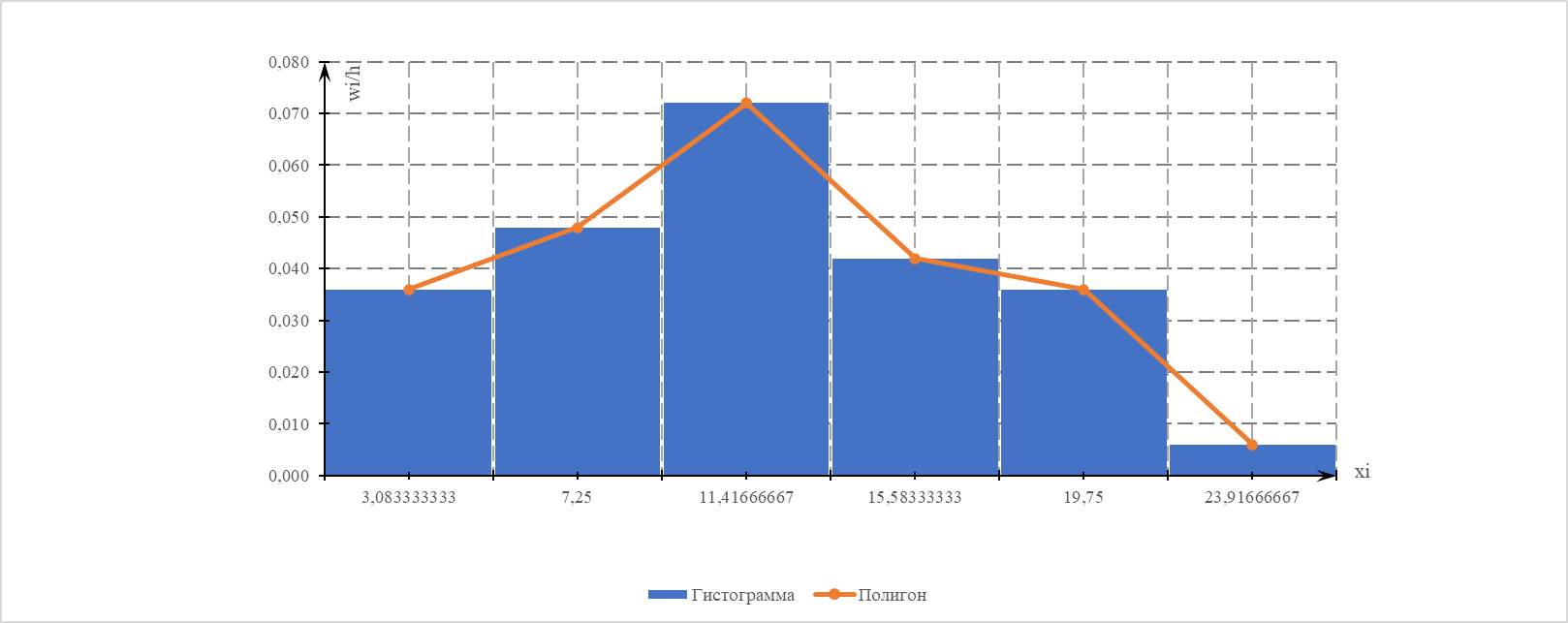



    Рис. 1. Гистограмма и полигон распределения

    При построении кумуляты в точках, соответствующих правому концу интервалов, по оси ординат откладываются накопленные частности mi, которые затем соединяются ломаной линией (рис. 2).



    Рис. 2. Кумулята распределения.

    2. Найдем выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение выборки.

    а) Вначале находим выборочное среднее, характеризующее центр распределения, около которого группируются выборочные данные, как взвешенное среднее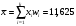



    Обозначая далее i xi  , где xi=(ai+bi)/2, вычисляем отклонения i варианты i x от среднего значения и заполняем таблицу:

    №
    xi
    wi
    ∆i
    xiwi
    ∆iwi
    ∆i2*wi

    0
    1
    2
    3
    4
    5
    6

    1
    3,083333333
    0,15
    -8,541666667
    0,4625
    -1,28125
    10,94401042

    2
    7,25
    0,2
    -4,375
    1,45
    -0,875
    3,828125

    3
    11,41666667
    0,3
    -0,208333333
    3,425
    -0,0625
    0,013020833

    4
    15,58333333
    0,175
    3,958333333
    2,727083333
    0,692708333
    2,741970486

    5
    19,75
    0,15
    8,125
    2,9625
    1,21875
    9,90234375

    K=6
    23,91666667
    0,025
    12,29166667
    0,597916667
    0,307291667
    3,777126736

    Σ
    -
    1
    -
    11,625
    0
    31,20659722

    Дисперсия выборочного распределения: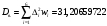

    Среднее квадратическое отклонение

    Вывод: гистограмма и полигон напоминают кривую нормального распределения, поэтому можно предположить (выдвинуть гипотезу), что генеральная совокупность, из которой взята выборка, относится к нормальному типу.

    написать администратору сайта