Подготовка к ОГЭ. Линейная и квадратичная функции. тесты КАШКА. Задание Найдите значение по графику функции, изображенному на рисунке. 1 2 3 4 Решение

• Название: Задание Найдите значение по графику функции, изображенному на рисунке. 1 2 3 4 Решение
• Анкор: Подготовка к ОГЭ. Линейная и квадратичная функции
• Дата: 06.04.2022
• Размер: 0.68 Mb.
• Имя файла: тесты КАШКА.docx
• Тип: Документы; #448837
• страница: 1 из 4

За­да­ние 1. Най­ди­те зна­че­ние   по гра­фи­ку функ­ции 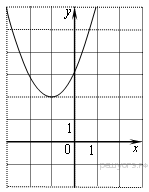 , изоб­ра­жен­но­му на ри­сун­ке.



 

1)

2)

3)

4)

 

 

Ре­ше­ние.

Абс­цис­са вер­ши­ны па­ра­бо­лы равна −1, по­это­му   от­ку­да   Па­ра­бо­ла пе­ре­се­ка­ет ось ор­ди­нат в точке с ор­ди­на­той 3, по­это­му   Тем самым, урав­не­ние па­ра­бо­лы при­ни­ма­ет вид   По­сколь­ку па­ра­бо­ла про­хо­дит через точку (−1; 2), имеем:

 



 

Вер­ный ответ ука­зан под но­ме­ром 2.

 

Ответ: 2.

За­да­ние 2. Най­ди­те зна­че­ние   по гра­фи­ку функ­ции 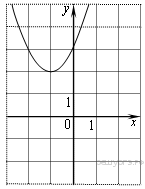 , изоб­ра­жен­но­му на ри­сун­ке.



 

1)

2)

3)

4)

 

 

Ре­ше­ние.

Абс­цис­са вер­ши­ны па­ра­бо­лы равна −1, по­это­му   от­ку­да   Па­ра­бо­ла пе­ре­се­ка­ет ось ор­ди­нат в точке с ор­ди­на­той 3, по­это­му   Тем самым, урав­не­ние па­ра­бо­лы при­ни­ма­ет вид   По­сколь­ку па­ра­бо­ла про­хо­дит через точку (−1; 2), имеем:

 



 

Таким об­ра­зом,



 

Вер­ный ответ ука­зан под но­ме­ром 3.

 

Ответ: 3.

За­да­ние 3. Най­ди­те зна­че­ние   по гра­фи­ку функ­ции 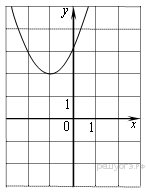  изоб­ра­жен­но­му на ри­сун­ке.

1)

2)

3)

4)

Ре­ше­ние.

Зна­че­ние   — это зна­че­ние гра­фи­ка при ор­ди­на­та гра­фи­ка при   Зна­чит,   Такой ответ ука­зан под но­ме­ром 4.

 

Ответ: 4.

За­да­ние 4. Най­ди­те зна­че­ние   по гра­фи­ку функ­ции 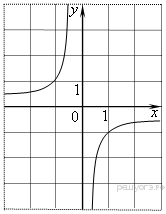  изоб­ра­жен­но­му на ри­сун­ке.



Ре­ше­ние.

По­сколь­ку ги­пер­бо­ла про­хо­дит через точку (−1; 1), имеем: 

 

Ответ: −1.

За­да­ние 5. На ри­сун­ке изоб­ражён гра­фик функ­ции 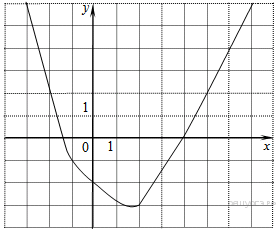  . Какие из утвер­жде­ний от­но­си­тель­но этой функ­ции не­вер­ны? Ука­жи­те их но­ме­ра.



 

1) функ­ция воз­рас­та­ет на про­ме­жут­ке  

2) 

3) 

4) пря­мая     пе­ре­се­ка­ет гра­фик в точ­ках     и  

 

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

Ре­ше­ние.

Про­ве­рим каж­дое из утвер­жде­ний.

1) Функ­ция воз­рас­та­ет на про­ме­жут­ке    — не­вер­но, функ­ция убы­ва­ет на про­ме­жут­ке   и затем воз­рас­та­ет на  .

2)   — не­вер­но,   

3)   — верно, видно из гра­фи­ка.

4) Пря­мая     пе­ре­се­ка­ет гра­фик в точ­ках     и    — верно, видно из гра­фи­ка.

Таким об­ра­зом, не­вер­ные утвер­жде­ния на­хо­дят­ся под но­ме­ра­ми 1 и 2.

 

Ответ: 1; 2.

За­да­ние 6. На ри­сун­ке изоб­ражён гра­фик квад­ра­тич­ной функ­ции y = f(x).

Какие из сле­ду­ю­щих утвер­жде­ний о дан­ной функ­ции не­вер­ны? За­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.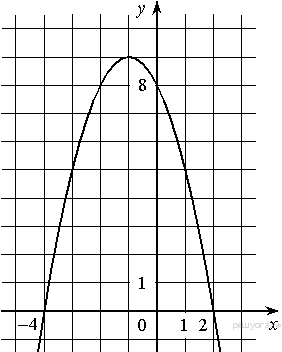

 



 

1) Функ­ция воз­рас­та­ет на про­ме­жут­ке (−∞;  −1].

2) Наи­боль­шее зна­че­ние функ­ции равно 8.

3) f(−4) ≠ f(2).

Ре­ше­ние.

Про­ве­рим каж­дое утвер­жде­ние.

1) На луче (−∞;  −1] боль­ше­му зна­че­нию ар­гу­мен­та со­т­вет­ству­ет боль­шее зна­че­ние функ­ции. Сле­до­ва­тель­но, функ­ция воз­рас­та­ет на этом луче; пер­вое утвер­жде­ние верно.

2) Наи­боль­шее зна­че­ние функ­ции равно 9. Вто­рое утвер­жде­ние не­вер­но.

3) Зна­че­ния фунц­кии в точ­ках −4 и 2 равны нулю, по­это­му f(−4) = f(2). Тре­тье утвер­жде­ние не­вер­но.

 

Ответ: 23.

За­да­ние 7. На ри­сун­ке изоб­ражён гра­фик квад­ра­тич­ной функ­ции y = f(x).

Какие из сле­ду­ю­щих утвер­жде­ний о дан­ной функ­ции не­вер­ны? За­пи­ши­те их но­ме­ра.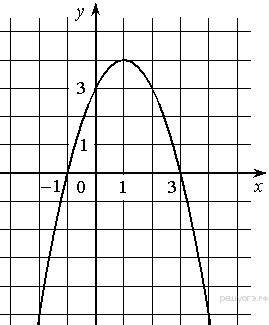

 



 

1) f(−1) = f(3).

2) Наи­боль­шее зна­че­ние функ­ции равно 3.

3) f(x)>0 при −1<x<3.

Ре­ше­ние.

Про­ве­рим каж­дое утвер­жде­ние.

1) f(−1) = f(3). Пер­вое утвер­жде­ние верно.

2) Наи­боль­шее зна­че­ние функ­ции равно 4. Вто­рое утвер­жде­ние не­вер­но.

3) f(x)>0 при −1<x<3. Тре­тье утвер­жде­ние верно.

 

Ответ: 2.

За­да­ние 8. На ри­сун­ке изоб­ражён гра­фик квад­ра­тич­ной функ­ции y = f(x).

Какие из сле­ду­ю­щих утвер­жде­ний о дан­ной функ­ции не­вер­ны? За­пи­ши­те их но­ме­ра.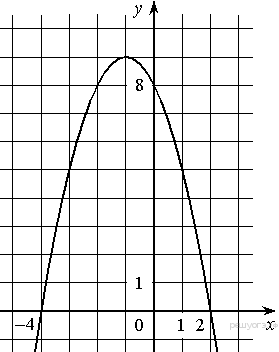

 



 

1) Наи­боль­шее зна­че­ние функ­ции равно 9.

2) f(0)>f(1).

3) f( x )>0 при x<0.

Ре­ше­ние.

Про­ве­рим каж­дое утвер­жде­ние.

 

1) Наи­боль­шее зна­че­ние функ­ции равно 9. Пер­вое утвер­жде­ние верно.

2) Зна­че­ния фунц­кии в точ­ке 0 равно 8, а в точке 1 — 5 по­это­му f(0) > f(1). Вто­рое утвер­жде­ние верно.

3) На луче (−∞;  0) функ­ция при­ни­ма­ет как по­ло­жи­тель­ные так и от­ри­ца­тель­ные зна­че­ния. Тре­тье утвер­жде­ние не­вер­но.

 

Ответ: 3.

За­да­ние 9. На ри­сун­ке изоб­ражён гра­фик функ­ции y = ax² + bx + c . Уста­но­ви­те со­от­вет­ствие между утвер­жде­ни­я­ми и про­ме­жут­ка­ми, на ко­то­рых эти утвер­жде­ния вы­пол­ня­ют­ся. Впи­ши­те в при­ведённую в от­ве­те таб­ли­цу под каж­дой бук­вой со­от­вет­ству­ю­щую цифру.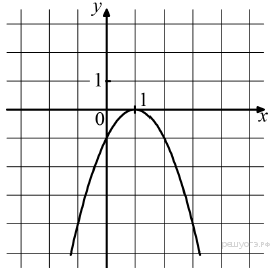



 

 

УТВЕР­ЖДЕ­НИЯ		ПРО­МЕ­ЖУТ­КИ
А) функ­ция воз­рас­та­ет на про­ме­жут­ке Б) функ­ция убы­ва­ет на про­ме­жут­ке		1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3]

 

Ответ:

Ре­ше­ние.

Функ­ция, изоб­ражённая на гра­фи­ке воз­рас­та­ет на про­ме­жут­ке   и убы­ва­ет на про­ме­жут­ке   Сле­до­ва­тель­но, на дан­ных про­ме­жут­ках функ­ция воз­рас­та­ет на тре­тьем про­ме­жут­ке и убы­ва­ет на пер­вом.

 

Ответ: 31.

За­да­ние 10. На ри­сун­ке изоб­ражён гра­фик функ­ции вида 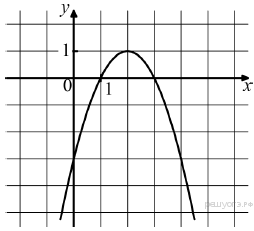 . Уста­но­ви­те со­от­вет­ствие между утвер­жде­ни­я­ми и про­ме­жут­ка­ми, на ко­то­рых эти утвер­жде­ния вы­пол­ня­ют­ся. Впи­ши­те в при­ведённую в от­ве­те таб­ли­цу под каж­дой бук­вой со­от­вет­ству­ю­щую цифру.

 

УТВЕР­ЖДЕ­НИЯ		ПРО­МЕ­ЖУТ­КИ
А) функ­ция воз­рас­та­ет на про­ме­жут­ке Б) функ­ция убы­ва­ет на про­ме­жут­ке		1) [0; 3] 2) [−1; 1] 3) [2; 4] 4) [1; 4]

 

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б

Ре­ше­ние.

Функ­ция воз­рас­та­ет, если боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет боль­шее зна­че­ние функ­ции. Функ­ция убы­ва­ет, если боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет мень­шее зна­че­ние функ­ции. Дан­ная функ­ция воз­рас­та­ет на про­ме­жут­ке   и убы­ва­ет на про­ме­жут­ке   Таким об­ра­зом, из при­ведённых про­ме­жут­ков функ­ция толь­ко воз­рас­та­ет на про­ме­жут­ке   убы­ва­ет на про­ме­жут­ке 

 

Ответ: 23.

За­да­ние 11. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = ax² + bx + c. Для каж­до­го гра­фи­ка ука­жи­те со­от­вет­ству­ю­щее ему зна­че­ния ко­эф­фи­ци­ен­та a и дис­кри­ми­нан­та D.

 

Гра­фик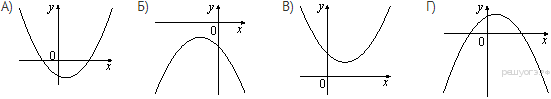

 



 

Знаки чисел

 

1) a > 0, D > 0

2) a > 0, D < 0

3) a < 0, D > 0

4) a < 0, D < 0

 

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В	Г