Параллельная работа синхронных генераторов

• Название: Параллельная работа синхронных генераторов
• Дата: 17.05.2023
• Размер: 3.19 Mb.
• Имя файла: mashiny_2_chast_ (1).doc
• Тип: Документы; #1138650
• страница: 7 из 11

§ 9.5. Электродвижущие силы и токи в обмотках статора и ротора при

вращающемся роторе.

При вращении ротора э. д. с. и токи в роторе будут изменяться в зависимости от величины скольжения. В неподвижном роторе э. д. с.






Во вращающемся роторе э. д. с

или

Частота тока в роторе уменьшается по мере роста скорости вращения ротора, так как f₂=f₂(n₁-n₂)/n₂,и э. д. с, наводимая в обмотке ротора при холостом ходе, может быть весьма мала, всего (0,03÷0,05) E_z.
Т ок в роторе двигателя так же, как и ток обмотки статора, соз­дает магнитный поток рассеяния, замыкающийся вокруг витков об­мотки ротора. Этот поток наводит в обмотке ротора реактивную э. д. с.

Реактивное сопротивление обмотки вращающегося ротора



По закону Ома ток в неподвижном роторе




Соответственно во вращающемся роторе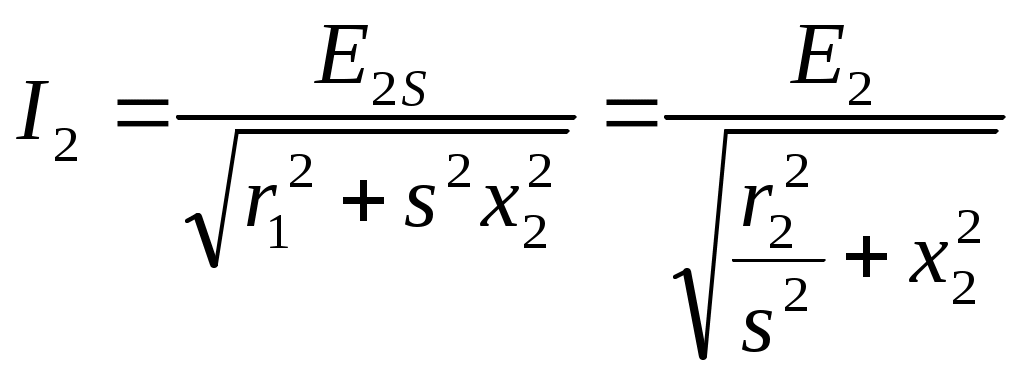






или


Ток обмотки ротора I₂ создает магнитный поток Ф₂, который вращается относительно ротора со скоростью п'₁= п₁—п₂.

Скорость вращения самого ротора равна п₂, тогда скорость вра­щения поля ротора в пространстве, т. е. относительно неподвиж­ного ротора,

п_пр =п'₂ + п₂ = п₁ - п₂ + п₂=п₁

Таким образом, поле ротора вращается в пространстве с той же скоростью и в ту же сторону, что и поле статора, и образует с ним общее результирующее поле. Благодаря этому, независимо от ско­рости вращения ротора, м. д. с. статора и ротора геометрически складываются, образуя полезный магнитный поток, т. е.







где м.д.с. статора при холостом ходе.
Аналогично трансформатору с помощью приведенных величин Е'₂, I'₂, r'₂и x'₂ для асинхронного двигателя можно построить векторную диаграмму (рис. 9.5, а) и схему замещения (рис. 9.5, б). Эта схема не вполне аналогична схеме замещения трансформатора, изображенной на рис. 8.8. Нетрудно видеть, что на этом рисунке r'₂=const, в то время как приведенное активное сопротивление об­мотки ротора r'₂ делится на переменную величину s, следовательно, и r₂ /s будет переменной величиной. Чтобы схема замещения стала вполне аналогичной схеме замещения трансформатора, произведем

несложное преобразование. Заменим величину r’₂/s суммой двух величин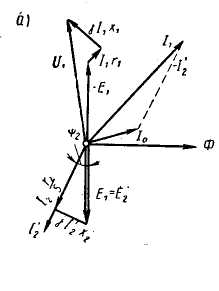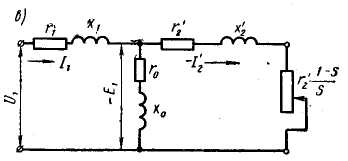




Рис. 9.5. Векторная диаграмма и схема замещения асинхрон­ного двигателя

Тогда схема замещения будет соответствовать схеме замещения трансформатора, вторичная обмотка которого нагружена на соп­ротивление r’₂(1-s/s) (рис.,9.5, в); r’₂является постоянным по величине активным сопротивлением обмотки ротора Величина r’₂(1-s/s) соответствует той части мощности, которая преобразуется в механическую.

§ 9.6. Потери и коэффициент полезного действия асинхронных двигателей

Электрическая мощность, подводимая к обмотке статора двига­теля, преобразуется в механическую мощность на его валу. Элек­трическая мощность больше механической на величину потерь.

На рис. 9.6 приведена энергетическая диаграмма асинхронного двигателя. В асинхронных двигателях имеют место: потери на на­грев обмоток статора и ротора (потери в меди) Р_M; потери магнит­ные на гистерезис и вихревые токи (потери в стали) Р_CТ и механичес­кие потери на трение Рмех.

Величина потерь в меди: для статора



д ля ротора


Для трехфазного двигателя с контактными кольцами число фаз m₁=m₂=3, для трехфазного двигателя с короткозамкнутым ротором m₂=Z_{2 .} При расчете потерь следует иметь ввиду, что активное сопротивление обмоток статора двигателей переменного тока несколько больше их омического сопротивления вследствие наличия поверхностного эффекта.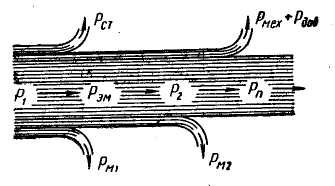


Рис 9.6. Энергетическая диаграмма асинхронного двигателя
Это увеличение сопротивления при стандартной частоте тока 50 гц может быть учтено коэффициентом, равным в среднем 1.1-1.2.

Сопротивление обмотки ротора близко к его омическому сопротивлению, так как частота тока в роторе при номинальном режиме работы очень незначительна (f₂=f_1S). Магнитные потери в стали ротора можно не учитывать ввиду их небольшой велечины.

Механические потери складываются из потерь на трение вра­щающихся частей машины о воздух, на трение в подшипниках и вентиляционных потерь. У двигателей с контактными кольцами прибавляются еще потери на трение щеток о контактные кольца.

Мощность, подводимая к трехфазному двигателю,



где U₁и I₁ — фазные напряжение и ток статора.

Мощность, передаваемая ротору посредством вращающегося магнитного поля, является электромагнитной мощностью;



Эта мощность может быть представлена как произведение вращаю­щегося момента электромагнитных сил на угловую скорость, т. е.



М
еханическая мощность на валу ротора, т. е. полезная мощность Двигателя, если пренебречь механическими потерями Р_ыех, которые в сравнении с другими потерями малы,

так как n₂=n₁(1-s)


Разность между Р_эм и P₂ представляет собой потери в обмотке ротора (потери в меди):



Отсюда следует, что скольжение ротора пропорционально потерям в его обмотке и является мерой этих потерь.

Потери в стали и механические потери почти не зависят от на­грузки (постоянные потери); они могут быть определены на основа­нии опыта холостого хода.

Потери в обмотках ротора и статора зависят от нагрузки (пе­ременные потери). Они определяются на основании опыта короткого замыкания (см. § 9.9). По отношению к номинальной мощности эти потери составляют примерно от 7 до 2,5%. Механические потери и потери в стали в значительной степени зависят от чис­ла полюсов двигателя и его мощности. Ниже, в табл. 9.1 приве­дены некоторые значения (в процентах к номинальной мощно­сти) постоянных потерь в зависимости от нагрузки для асинхрон­ных двигателей типа А и А2.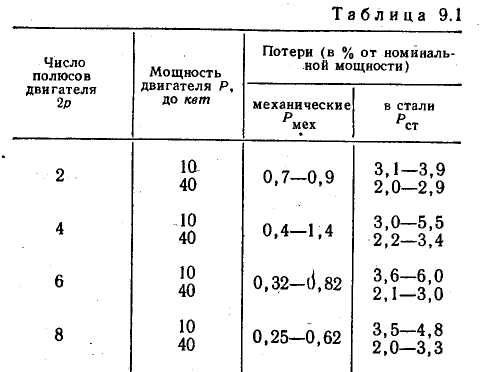



В асинхронных машинах имеются также и добавочные потери. По ГОСТ 183-55 для этого типа машин добавочные потери прини­маются равными 0,5% номинальной мощности.

Таким образом, суммарные потери асинхронных двигателей



К оэффициент полезного действия двигателя представляет собой отношение полезной мощности, развиваемой на валу, к полной мощ­ности, т. е.

и ли

§ 9.7. Электромагнитный момент асинхронного двигателя

Электромагнитный момент асинхронного двигателя создается в результате взаимодействия тока в обмотке ротора с вращающимся магнитным полем статора. Величина в ращающегося момента оп­ределяется из выражения для электромагнитной мощности




Здесь или подставляя значение


В 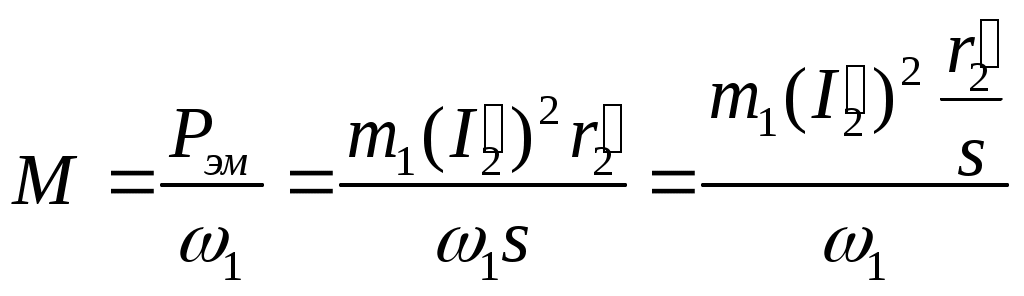ыше было показано, что мощность электромагнитных потерь в об­мотке ротора пропорциональна скольжению (P_Mi=P_auS) и равна отсюда



Таким образом, вращающий момент двигателя пропорционален электрическим потерям в роторе.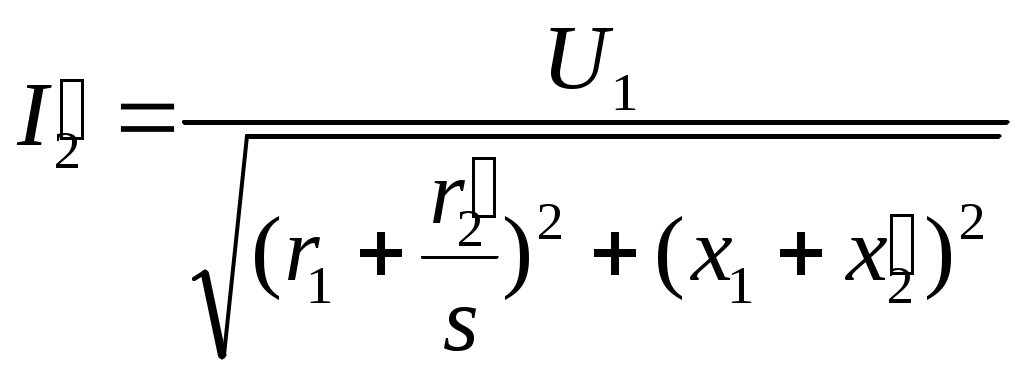

Приведенный ток в роторе
Подставляя это значение тока в уравнение момента, получаем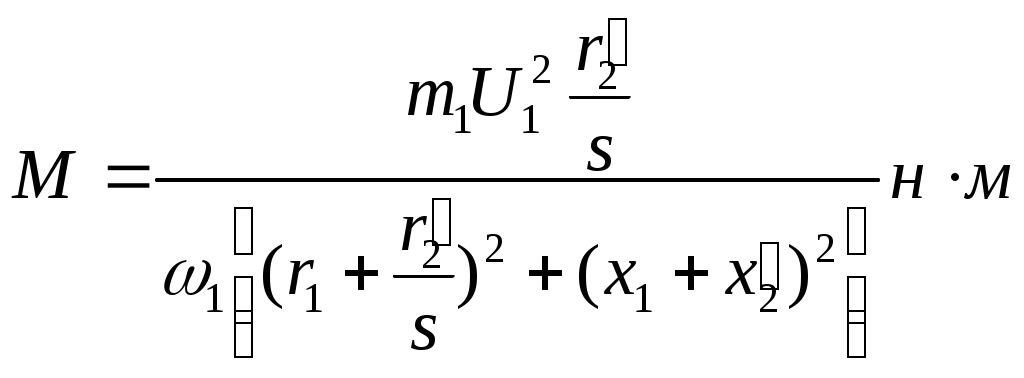




Если, в уравнении вращающего момента (х₁+х₂') выразить через х и умножить числитель и знаменатель на s², то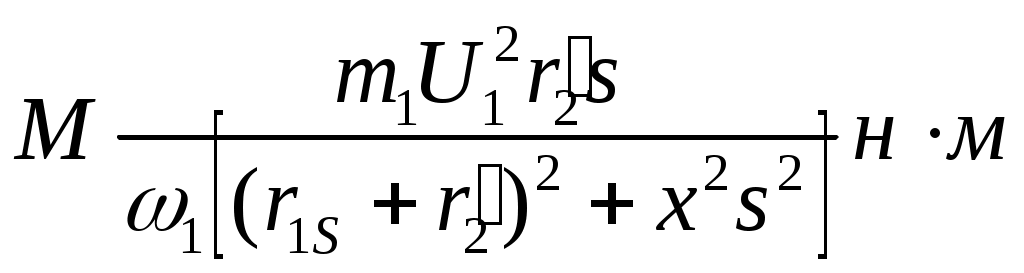



П 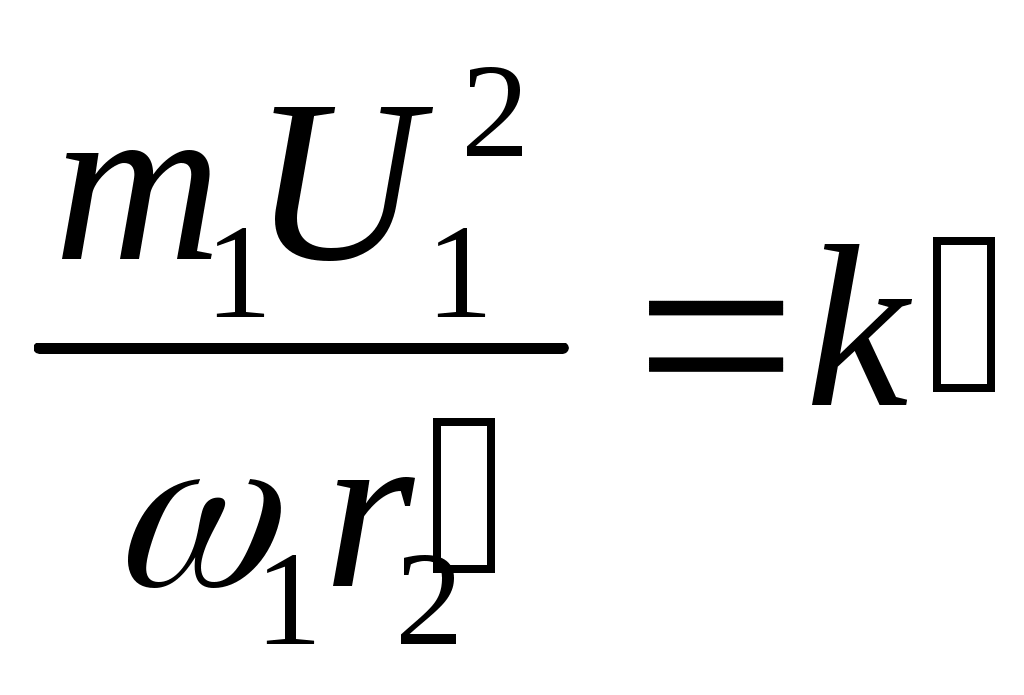ри небольших значениях скольжения, в пределах 1,5% его номи­нального значения, величинами r₁sи x²s²можно пренебречь. Тогда. пологая получим



Таким образом в пределах до номинальной нагрузки момент двигателя прямо пропорционален скольжению. С увеличением скольжения момент растет, но лишь до определенного максимального значения М_МАКС, соответствующего некоторому значению S_КР=
=0,12 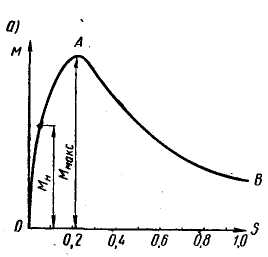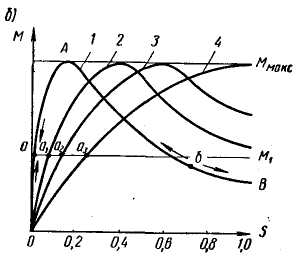0,20.




Рис. 9.7. Кривые зависимости M=f(s)



На основании выражения (9.8) строим график зависимости электромагнитного момента машины от скольжения при постоянном подведенном напряжении U₁=constи частоте тока f_t=const(рис. 9.7, а). Эта зависимость называется механической характери­стикой двигателя. Параметры m₁r₁r’₂x₂и х’₂, входящие в урав­нение (9.8), являются величинами, постоянными для данной ма­шины, так как они задаются конструкцией двигателя.

В момент пуска двигателя n₂=0 и s=l. Под действием началь­ного пускового момента, если он достаточен для преодоления ста­тического момента, ротор двигателя начинает вращаться, и ско­рость его будет увеличиваться до тех пор, пока вращающий момент не уравняется со статическим. По мере разгона двигателя скольже­ние уменьшается. С уменьшением sодновременно увеличивается как числитель, так и знаменатель, но вначале числитель растет в большей степени, чем знаменатель, поэтому момент увеличивает­ся. При критическом значении скольжения



вращающий момент достигает наибольшего значения M_макс. В дальнейшем начинает сказываться преобладающее значение зна­менателя, куда r₂/xвходит в квадрате, и момент постепенно умень­шается и при s=0 станет равным нулю.

Механическую характеристику можно разделить на два участ­ка- устойчивой (ОА) и неустойчивой (АВ) работы. Если считать, что противодействующий момент механизма, приводимого в дей­ствие данным двигателем, не зависит от скорости вращения, т. е. M_CT=const, то зависимость M_CT=f(s) будет выражаться прямой, параллельной оси абсцисс.

Предположим, что при данном моменте M₁ устойчивая работа двигателя (M₁=M₀+M₂=М_ст) определяется точкой а на кривой 1 (рис. 9.7, б). Если по какой-либо причине момент М₁окажется больше момента М_СТ, скорость вращения двигателя уменьшится (скольжение увеличится), и устойчивый режим двигателя восста­новится в той же точке а , но уже при меньшей скорости вращения. Если же нарушение устойчивого режима двигателя произойдет в точке б, то при M_CT>М₁ скорость вращения двигателя будет снижаться до полной остановки последнего. При M_CТ<М₁, на­оборот, скорость двигателя увеличится до значения, при котором двигатель войдет вобласть устойчивой работы, определяемой для данного случая точкой а.

Величина максимального момента определяется значением кри­тического скольжения

Подставляя значение s_Kp в выражение момента (9.8), получаем уравнение максимального вращающего момента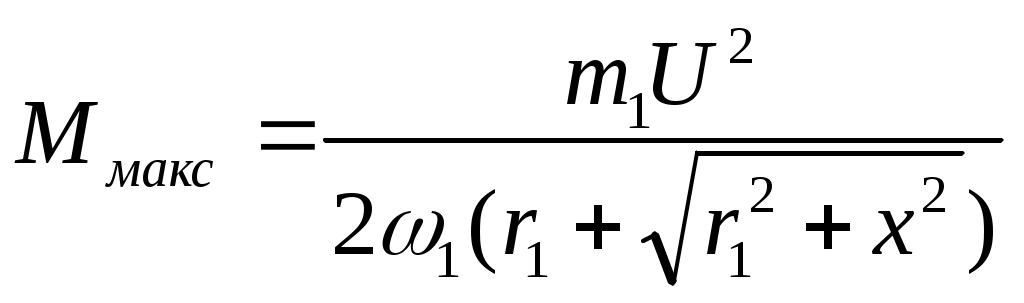



Ввиду того, что в формуле (9.11) r₁весьма мало по сравнению с х, то можно записать



Выражения (9.10) и (9.11) дают возможность сделать выводы:

а) чем больше r’₂/x тем большее скольжение будет соответство­вать максимальному вращающему моменту;

б) максимальное значение момента не зависит от активного со­противления ротора r’₂;

в) максимальное значение момента пропорционально квадрату напряжения, подводимого к статору (М_МАКС ).

Отсюда следует, что если у асинхронного двигателя увеличивать активное сопротивление ротора r₂', то максимальный момент, сох­раняя свое значение, будет смещаться в сторону больших скольже­ний (рис. 9.7, б, кривые 2, 3 и 4).

Ток ротора I’₂, как известно, вследствие индуктивности обмот­ки ротора, отстает по фазе от э. д. с. Е₂на некоторый угол .Из векторной диаграммы (см. рис. 9.5, а) в идно, что

где — угол сдвига между Е'₂н I₂'. Подставляя это значение в формулу (9.7), получим


Н о E’₂=E₁. Подставив вместо Е’₂значение E₁ из формулы (9.4), получим
Дробь является постоянной величиной, обозначим ее через k_M, тогда



Таким образом, выражение момента асинхронного двигателя от­личается от выражения момента машин постоянного тока множи­телем так же, как и формула мощности отличается от фор­мулы мощности машин постоянного тока тем же множителем.

Т ак как при работе асинхронного двигателя под нагрузкой изменяется мало и близок к единице, то приближенно можно напи­сать


В начальный момент пуска асинхронного двигателя при непод­вижном еще роторе относительная скорость вращающегося магнит­ного поля и индуктивное сопротивление х будут максимальны, а — минимален. Поэтому момент асинхронного двигателя сравнительно невелик, несмотря на большой ток в роторе. Между тем, при пуске двигателя под нагрузкой часто желательно иметь наи­больший момент, который может быть получен лишь при условии равенства активного сопротивления вторичной цепи г₂ индуктив­ному сопротивлению двигателя х, т. е. когда r’₂/x=1 или r'₂=х.

С опротивление обмотки ротора г₂' меньше индуктивного со­противления х. У двигателей с контактными кольцами оно может быть повышено введением в цепь ротора пускового реостата. Соп­ротивление реостата подбирается с таким расчетом, чтобы

В момент пуска добавочное сопротивление реостата позволяет получить максимальный момент при s=l, т. е. получить М_пуск = M_МАКС

Кривые зависимости M=f(s) для. разных значений г₂' по­зволяют рассчитать процесс пуска асинхронного двигателя и сек­ции пускового реостата для двигателя с контактными кольцами.

Д ля устойчивой работы двигателя необходимо, чтобы его мак­симальный момент был больше номинального, т. е. чтобы двигатель обладал перегрузочной способностью. У асинхронных двигателей единой серии типа А и АО перегрузочная способность


Как отмечалось, максимальный вращающий момент асинхрон­ных двигателей пропорционален квадрату напряжения. Поэтому при снижении напряжения, например, на 30%, т. е. при U₁= =0,7U_H момент М '_МАКС будет равен всего 0,7²М_МАКС и может оказать­ся меньше номинального. В этом случае работа двигателя с номи­нальной нагрузкой уже невозможна.