Введение, Гл 1-5. в назначение электрических машин и трансформаторов

• Название: в назначение электрических машин и трансформаторов
• Дата: 08.11.2022
• Размер: 2.87 Mb.
• Имя файла: Введение, Гл 1-5.doc
• Тип: Документы; #777052
• страница: 9 из 20

§ 1.9. Явления при намагничивании магнитопроводов трансформаторов

Допустим, что к первичной обмотке трансформатора подведено синусоидальное напряжение. При этом поток в магнитопроводе также будет синусоидальным: Ф = Ф_mах sinωt. Однако вследствие насыщения магнитный поток трансформатора не пропорционален намагничивающему току. Поэтому при синусоидальном потоке Ф намагничивающий ток ; является несинусоидальным. Для определения формы кривой этого тока i_Ор = f(t) воспользуемся кривой намагничивания магнитопровода Ф = f(i_Ор) и графиком изменения потока Ф =f(t).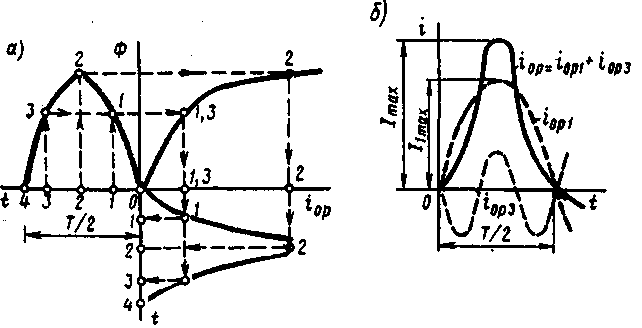



Рис. 1.23. Построение графика намагничивающего тока (а) и разложение его на составляющие (б)

На рис. 1.23, а дано построение графика намагничивающего тока i_0р ⁼ f(t). Здесь в левом верхнем квадранте показана синусоидальная кривая Ф =f(t), а в верхнем правом квадранте — кривая намагничивания Ф = f(i_0р) материала магнитопровода. Для получения графика намагничивающего тока i_0р = f(t), расположенного в правом нижнем квадранте, поступают следующим образом. На графике Ф = f(t) выбирают ряд точек 7, 2, 3, проецируют их на кривую намагничивания и определяют значения намагничивающего тока, соответствующие выбранным значениям магнитного потока. Затем проводят вертикальные линии через точки 1, 2, 3 на оси i_0р в правый нижний квадрант до пересечения с горизонтальными линиями, проведенными из точек 1, 2, 3 на оси времени этого квадранта, и получают геометрическое место точек кривой намагничивающего тока i_0р = f(t). Из сделанных построений видно, что при синусоидальной форме кривой Ф =f(t) намагничивающий ток имеет пикообразную форму. В целях упрощения построений в этом случае воспользовались кривой намагничивания Ф = f(i_0р), построенной без учета гистерезиса.

После разложения несинусоидальной кривой тока i_0р на синусоидальные составляющие (рис. 1.23, б) видно, что в этом токе кроме основной (первой) гармоники i_0р1 ярко выражена третья гармоника i_0р3.

Так, в трансформаторе с магнитопроводом из высоколегированной стали при индукции В = 1,4 Тл амплитуда третьей гармоники составляет примерно 30% амплитуды основной гармоники намагничивающего тока. Сказанное относится лишь к реактивной составляющей тока х.х., так как активная составляющая i_0a является синусоидальной. Обычно i_0a не превышает 10% от I₀, поэтому с некоторым приближением можно принять, что кривая тока х.х. i₀=f(t) не отличается от кривой i_0р = f(t).

§ 1.10. Влияние схемы соединения обмоток на работу трехфазных трансформаторов в режиме холостого хода

Из уравнений токов третьей гармоники в трехфазной системе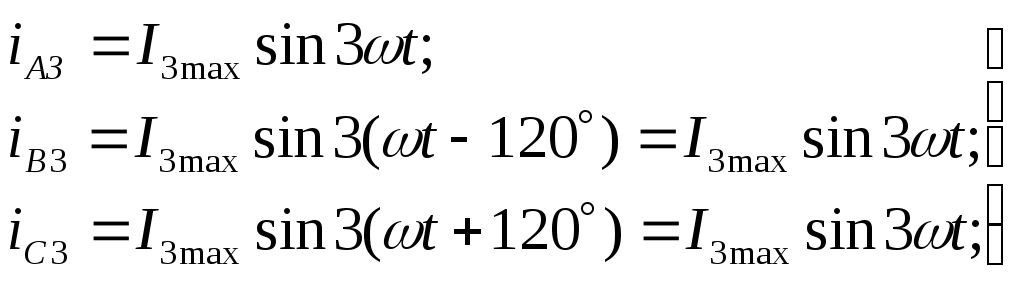

(1.37)

видно, что эти токи в любой момент времени совпадают по фазе, т. е. имеют одинаковое направление. Этот же вывод распространяется на все высшие гармоники тока, кратные трем, — 3, 9, 15 и т. д. Это обстоятельство оказывает существенное влияние на процессы, сопровождающие намагничивание сердечников при трансформировании трехфазного тока.

Рассмотрим особенности режима холостого хода трехфазных трансформаторов для некоторых схем соединения обмоток.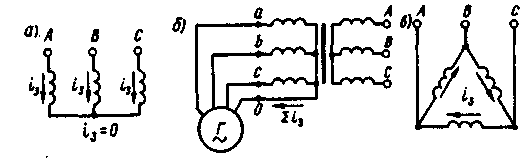



Рис. 1 .24. Направление токов третьей гармоники для различных схем соединения обмоток

Соединение Y/Y₀. Если напряжение подводится со стороны обмоток, соединенных звездой без нулевого вывода (рис. 1.24, а), то токи третьей гармоники (и кратные трем — 9, 15 и т. д.), совпадая по фазе во всех трех фазах, будут равны нулю. Объясняется это отсутствием нулевого провода, а следовательно, отсутствием выхода из нулевой точки. В итоге токи третьей и кратные трем гармоники будут взаимно компенсироваться и намагничивающий ток трансформатора окажется синусоидальным, но магнитный поток в магнитопроводе окажется несинусоидальным (уплощенным) с явно выраженным потоком третьей гармоники Ф_з (рис. 1.25).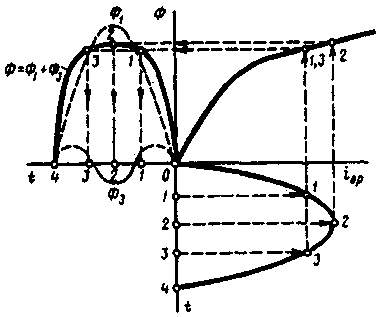



Рис. 1.25. Построение графика магнитного потока при синусоидальной форме намагничивающего тока

Потоки третьей гармоники не могут замкнуться в трехстержневом магнитопроводе, так как они совпадают по фазе, т.е. направлены встречно. Эти потоки замыкаются через воздух (масло) и металлические стенки бака (рис. 1.26). Большое магнитное сопротивление потоку Ф₃ ослабляет его величину, поэтому наводимые потоками Ф₃ в фазных обмотках ЭДС третьей гармоники невелики и обычно их амплитуда не превышает 5 — 7% от амплитуды основной гармоники. На практике поток Фз учитывают лишь с точки зрения потерь от вихревых токов, индуцируемых этим потоком в стенках бака. Например, при индукции в стержне магнитопровода порядка 1,4 Тл потери от вихревых токов в баке составляют около 10% от потерь в магнитопроводе, а при индукции 1,6 Тл эти потери возрастают до 50 — 65%.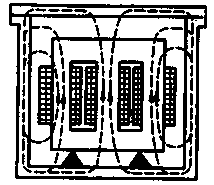



Рис. 1.26. Пути замыкания магнитных потоков третьей гармоники в трехстержневом магнитопроводе

В случае трансформаторной группы, состоящей из трех однофазных трансформаторов (см. рис. 1.20, а), магнитопроводы отдельных фаз магнитно не связаны, поэтому магнитные потоки третьей гармоники всех трех фаз беспрепятственно замыкаются (поток каждой фазы замыкается в своем магнитопроводе). При этом значение потока Фз может достигать 15 — 20% от Ф₁ Несинусоидальный магнитный поток Ф, содержащий кроме основной гармоники Ф₁ еще и третью Ф₃,

(1.38)

наводит в фазных обмотках несинусоидальную ЭДС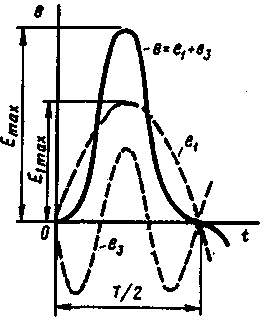

(1.39)



Рис. 1.27. Форма графика фазной ЭДС трансформаторной группы при соединении обмоток Y/Y

Повышенная частота Зω магнитного потока Ф₃ приводит к появлению значительной ЭДС е₃, резко увеличивающей амплитудное значение фазной ЭДС обмотки при том же ее действующем значении (рис.1.27), что создает неблагоприятные условия для электрической изоляции обмоток.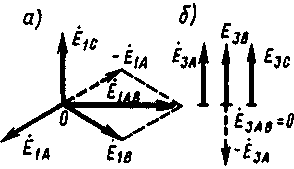



Рис. 1.28. Векторные диаграммы ЭДС основной (а) и третьей (б) гармоник трехфазного трансформатора

Амплитуда ЭДС третьей гармоники в трансформаторной группе может достигать 45—65% от амплитуды основной гармоники. Однако следует отметить, что линейные ЭДС (напряжения) остаются синусоидальными и не содержат третьей гармоники, так как при соединении обмоток звездой фазные ЭДС е_3A, е_3Bи е_зс, совпадая по фазе, не создают линейной ЭДС. Объясняется это тем, что линейная ЭДС при соединении обмоток звездой определяется разностью фазных ЭДС. Так, для основной гармоники (рис. 1.28, а) линейная ЭДС



Что же касается линейной ЭДС третьей и кратных трем гармоник, то ввиду совпадения по фазе фазных ЭДС этих гармоник (рис. 1.28, б) получим



Если первичная обмотка трансформатора является обмоткой НН и ее нулевой вывод присоединен к нулевому выводу генератора (см. рис. 1.24, б), то намагничивающие токи фаз содержат третьи гармоники. Эти токи совпадают по фазе [см.(1.37)], а поэтому все они направлены либо от трансформатора к генератору, либо наоборот. В нулевом проводе будет протекать ток, равный 3i_з. при этом магнитный поток трансформатора, а следовательно, и ЭДС в фазах будут синусоидальны.

Соединения, при которых обмотки какой-либо стороны трансформатора (НН или ВН) соединены в треугольник. Эти схемы соединения наиболее желательны, так как они лишены недостатков рассмотренных ранее схем.

Допустим, что в треугольник соединены первичные обмотки трансформатора. Тогда ток третьей гармоники беспрепятственно замыкается в замкнутом контуре фазных обмоток, соединенных в треугольник (см. рис. 1.24, в). Но если намагничивающий ток содержит третью гармонику, то магнитные потоки в стержнях, а следовательно, и ЭДС в фазах практически синусоидальны.

Если же вторичные обмотки трансформатора соединены в треугольник, а первичные — в звезду, то ЭДС третьей гармоники, наведенные во вторичных обмотках, создают в замкнутом контуре треугольника ток третьей гармоники. Этот ток создает в магнитопроводе магнитные потоки третьей гармоники Ф₂₃, направленные встречно потокам третьей гармоники от намагничивающего тока Ф₁₃ (по правилу Ленца). В итоге результирующий поток третьей гармоники значительно ослабляется и практически не влияет на свойства трансформаторов.

§ 1.11. Опытное определение параметров схемы замещения трансформаторов

Полученная в § 1.6 электрическая схема замещения (см. рис. 1.18, б) позволяет с достаточной точностью исследовать свойства трансформаторов в любом режиме. Использование этой схемы при определении характеристик имеет наибольшее практическое значение для трансформаторов мощностью 50 кВ-А и выше, так как исследование таких трансформаторов методом непосредственной нагрузки связано с некоторыми техническими трудностями: непроизводительным расходом электроэнергии, необходимостью в громоздких и дорогостоящих нагрузочных устройствах.

Определение параметров схемы замещения Z₁ = г₁ + jx₁, Z_m=r_m + jx_m, Z’₂=r₂'+jx'₂возможно либо расчетным (в процессе расчета трансформатора), либо опытным путем. Ниже излагается порядок определения параметров схемы замещения трансформатора опытным путем, сущность которого состоит в проведении опыта холостого хода (х.х.) и опыта короткого замыкания (к.з).

Опыт холостого хода. Холостым ходом называют режим работы трансформатора при разомкнутой вторичной обмотке (Z_н=∞, I₂ = 0). В этом случае уравнения напряжений и токов (1.34) принимают вид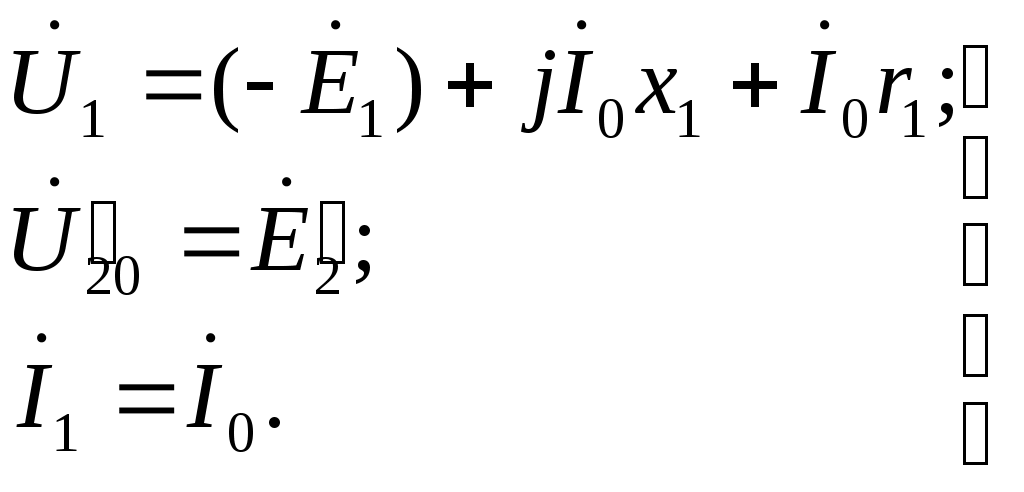

(1.40)

Так как полезная мощность при работе трансформатора вхолостую равна нулю, то мощность на входе трансформатора в режиме х.х. Р₀расходуется на магнитные потери в магнитопроводе Р_м, (потери на перемагничивание магнитопровода и вихревые токи) и электрические потери в меди I₀²r₁, (потери на нагрев обмотки при прохождении по ней тока) одной лишь первичной обмотки. Однако ввиду небольшого значения тока I₀, который обычно не превышает 2—10% от I_1ном, электрическими потерями I₀²r₁, можно пренебречь и считать, что вся мощность х.х. представляет собой мощность магнитных потерь в стали магнитопровода. Поэтому магнитные потери в трансформаторе принято называть потерями холостого хода (см. §1.14).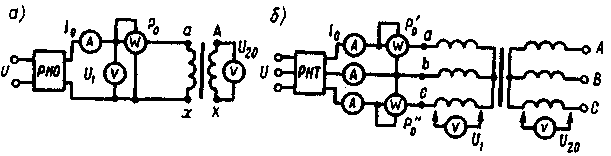



Рис. 1.29. Схемы опыта х.х. трансформаторов однофазного (а), трехфазного (б)

Опыт х.х. однофазного трансформатора проводят по схеме изображенной на рис. 1.29, а. Комплект электроизмерительных приборов, включенных в схему, дает возможность непосредственно измерить напряжение U₁, подведенное к первичной обмотке; напряжение U₂₀на выводах вторичной обмотки; мощность х х Р₀ и ток х.х. I₀.

Напряжение к первичной обмотке, трансформатора обычно подводят через однофазный регулятор напряжения РНО, позволяющий плавно повышать напряжение от 0 до 1,15U_1ном. При этом через приблизительно одинаковые интервалы тока х.х. снимают показания приборов, а затем строят характеристики х.х.: зависимости тока х.х. I_о, мощности х.х. Р₀и коэффициента мощности х.х. соsφ₀ от первичного напряжения U₁ (рис. 1.30).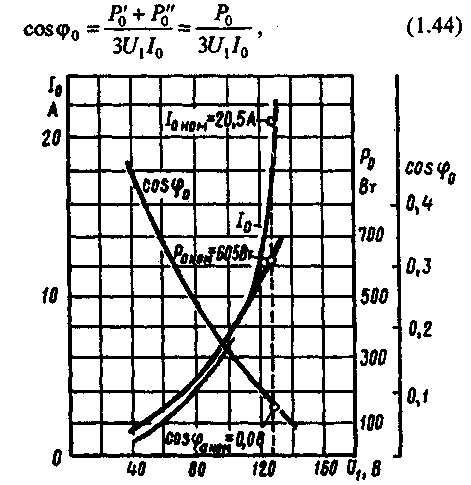

Рис. 1.30. Характеристики х.х. трансформатора

Криволинейность этих характеристик обусловлена состоянием магнитного насыщения магнитопровода, которое наступает при некотором значении напряжения U₁.

В случае опыта холостого хода с трехфазным трансформатором напряжение U₁устанавливают посредством трехфазного регулятора напряжения РНТ (рис. 1.29, б). Характеристики х.х. строят по средним фазным значениям тока и напряжения для трех фаз:


Рис. 1.30. Характеристики х.х. трансформатора
(1.41)

(1.42)

Коэффициент мощности для однофазного трансформатора

(1.43)

где P_о' и P_о" — показания однофазных ваттметров; U₁и I₀ — фазные значения напряжения и тока.

По данным опыта х.х. можно определить: коэффициент трансформации

k = U₁/U₂₀ = w_l/w₂;

ток х.х. при U_1ном (в процентах от номинального первичного тока)

i₀=(I_{о ном}/I_{1 ном})100; (1.45)

потери х.х. Р₀.

В трехфазном трансформаторе токи для трехфазного трансформатора х.х. в фазах неодинаковы и образуют несимметричную систему (см. § 1.8), поэтому мощность P_оследует измерять двумя ваттметрами по схеме, изображенной на рис. 1.29, б. Падение напряжения в первичной ветви схемы замещения в режиме х.х. I₀(r₁+jx₁) (рис. 1.31) составляет весьма незначительную величину, поэтому, не допуская заметной ошибки, можно пользоваться следующими выражениями для расчета параметров ветви намагничивания: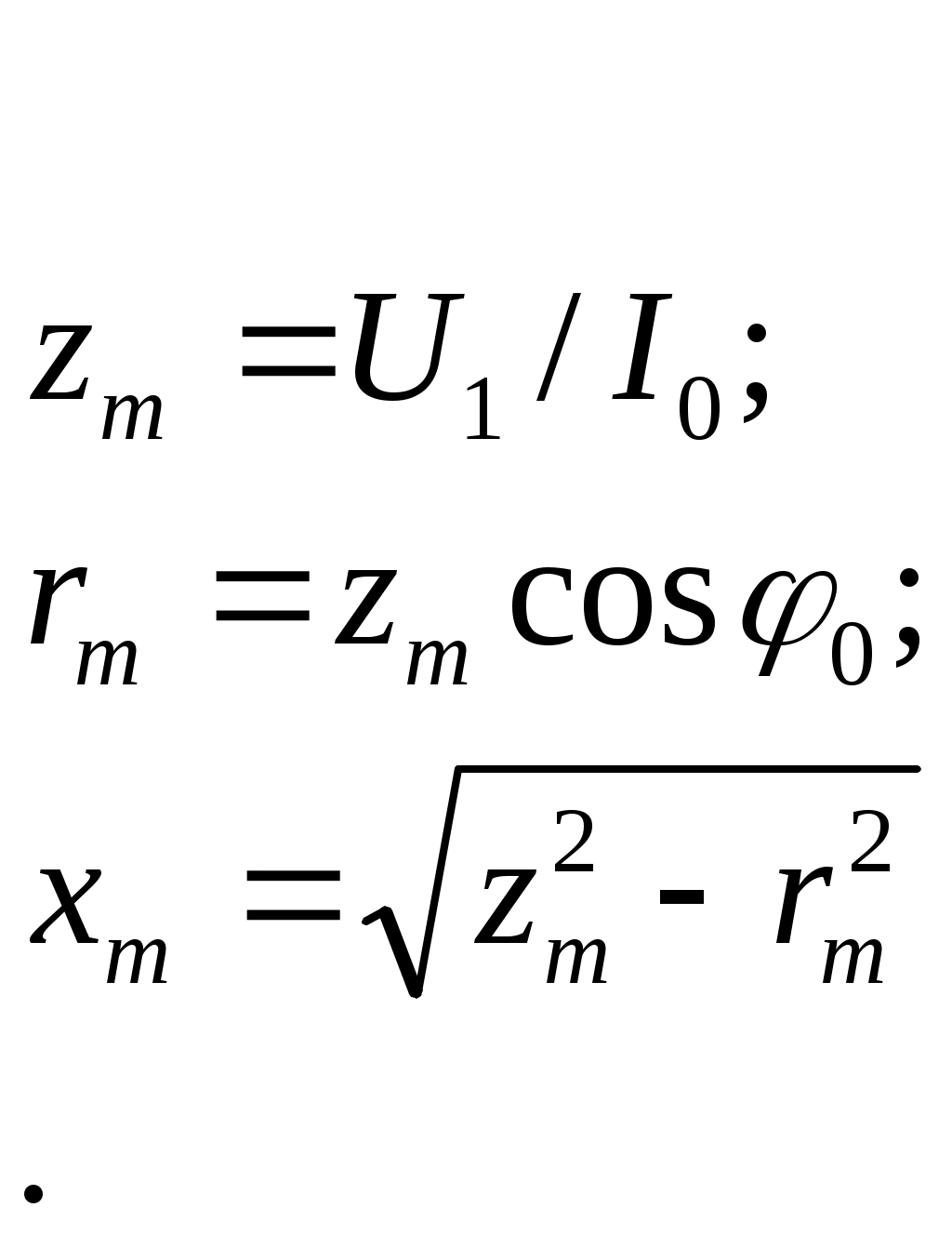


(1.46)

(1.47)

(1.48)


Обычно в силовых трансформаторах общего назначения средней и большой мощности при номинальном первичном напряжении ток х.х. i₀=10÷0,6%.

Если же фактические значения тока х.х. I_0ном и мощности х.х. P_0ном, соответствующие номинальному значению первичного напряжения U_1ном, заметно превышают величины этих параметров, указанные в каталоге на данный тип трансформатора, то это свидетельствует о неисправности этого трансформатора: наличие короткозамкнутых витков в обмотках либо замыкании части пластин магнитопровода.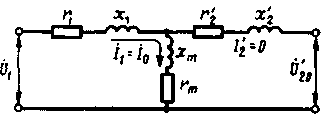



Рис. 1.31. Схема замещения трансформатора в режиме х.х.

Пример 1.4. На рис. 1.30 приведены характеристики холостого хода (I_{о ном}=20,5А; соsφ_0ном=0,08) трехфазного трансформатора с данными: S_ном=100кВ·А; U_lном,/U_2ном=6,3/0,22 кВ; соединение обмоток Y/Y. Определить параметры ветви намагничивания схемы замещения трансформатора z_m, r_m и х_ти ток холостого хода при номинальном фазном напряжении на стороне обмоток НН U_2ф = 127 В.

Решение. Полное сопротивление ветви намагничивания по (1.46)



активное сопротивление ветви намагничивания по (1.47) ,



индуктивное сопротивление ветви намагничивания по (1.48)



Ток холостого хода по (1.45)



где номинальное значение тока в обмотке НН



Здесь U_2ном— линейное значение вторичного напряжения.

Опыт короткого замыкания. Короткое замыкание трансформатора — это такой режим, когда вторичная обмотка замкнута накоротко (z_н = 0), при этом вторичное напряжение U₂ = 0. В условиях эксплуатации, когда к трансформатору подведено номинальное напряжение U_1ном, короткое замыкание является аварийным режимом и представляет собой большую опасность для трансформатора (см. § 4.1).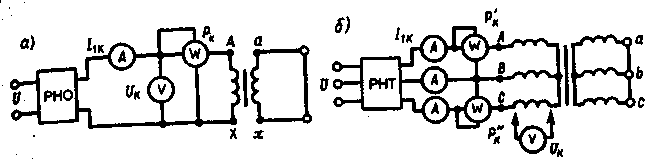



Рис. 1.32. Схемы опыта к.з. трансформаторов однофазного (а), трехфазного (6)

При опыте к.з. обмотку низшего напряжения однофазного трансформатора замыкают накоротко (рис. 1.32, а), а к обмотке высшего напряжения подводят пониженное напряжение, постепенно повышая его регулятором напряжения РНО до некоторого значения U_K.ном, при котором токи к.з. в обмотках трансформатора становятся равными номинальным токам в первичной ( I_1к = I_1ном) и вторичной (I_2к = I_2ном) обмотках. При этом снимают показания приборов и строят характеристики к.з., представляющие собой зависимость тока к.з. I_1К, мощности к.з. Р_ки коэффициента мощности cosφ_K от напряжения к.з. U_к(рис. 1.33).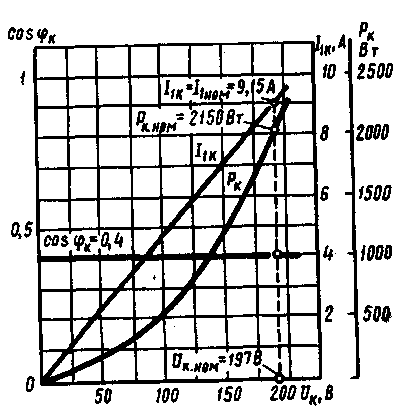



Рис. 1.33. Характеристики к.з. трансформатора

В случае трехфазного трансформатора опыт проводят по схеме, показанной на рис.1.32, б, а значения напряжения к.з. и тока к.з. определяют как средние для трех фаз:

(1.49)

(1-50)

Коэффициент мощности при опыте к.з.

cosφ_к= Р_к/(3 U_к I_1к) (1-51)

При этом активную мощность трехфазного трансформатора измеряют методом двух ваттметров. Тогда мощность к.з.

(1-52)

В (1.52) P_K и Р_K — показания однофазных ваттметров, Вт.

Напряжение, при котором токи в обмотках трансформатора при опыте равны номинальным значениям, называют номинальным напряжением короткого замыкания и обычно выражают его в % от номинального:

u_к=(Uк/U_1ном)100 (1.53)

Для силовых трансформаторов u_к = 5-10% от U_1HOM.

Как следует из (1.20), магнитный поток в магнитопроводе трансформатора пропорционален первичному напряжению U₁. Но так как это напряжение при опыте к.з. составляет не более 10% от U_1HOM, то такую же небольшую величину составляет магнитный поток. Для создания такого магнитного потока требуется настолько малый намагничивающий ток, что значением его можно пренебречь. В этом случае уравнение токов (1.24) принимает вид

(1.54)

а схема замещения трансформаторов для опыта к.з. не содержит ветви намагничивания (рис. 1.34, а). Для этой схемы замещения можно записать уравнение напряжений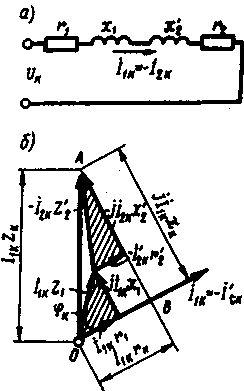



Рис. 1.34. Схема замещения (а) и векторная диаграмма (б) трансформатора в режиме к.з.

, (1.55)

или

(1.56)

Полное сопротивление трансформатора при опыте к.з.

Z_K=r_K+jx_k, (1.57)

где г_к и x_k — активная и индуктивная составляющие сопротивления к.з. Z_K.

Воспользовавшись уравнениями токов (1.54) и напряжений (1.55), для опыта к.з. построим векторную диаграмму трансформатора (рис. 1.34, б). Построение этой диаграммы начинают с вектора напряжения к.з. U_K = I_1KZ_K. Затем под углом φ_к к вектору U_Kпроводят вектор тока к.з. I_1K = –I_2K. Построив векторы падений напряжения в первичной обмотке I_1Kr₁, и jI_1Kx₁, и векторы падения напряжения во вторичной обмотке –I’_2Kr’₂ и –j I’_2Kx’_2,получают прямоугольный треугольник АОВ, называемый треугольником короткого замыкания. Стороны этого треугольника будут: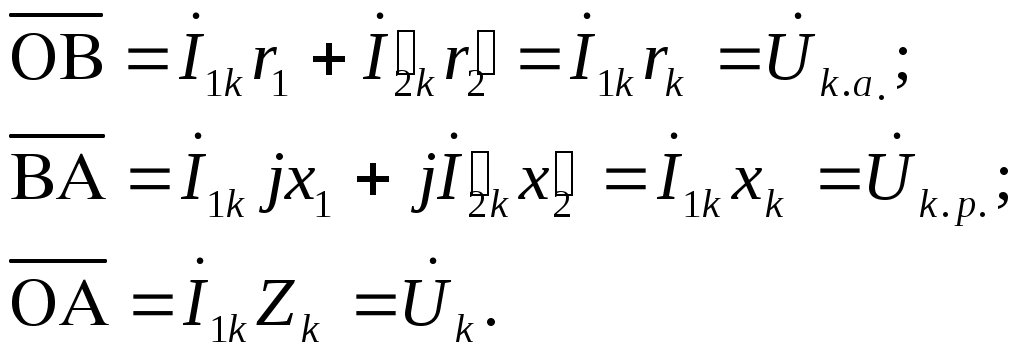



Здесь

(1.58)

где U_к.а U_к.р — активная и реактивная составляющие напряжения к.з., В.

Полное, активное и индуктивное сопротивления схемы замещения при опыте к.з.: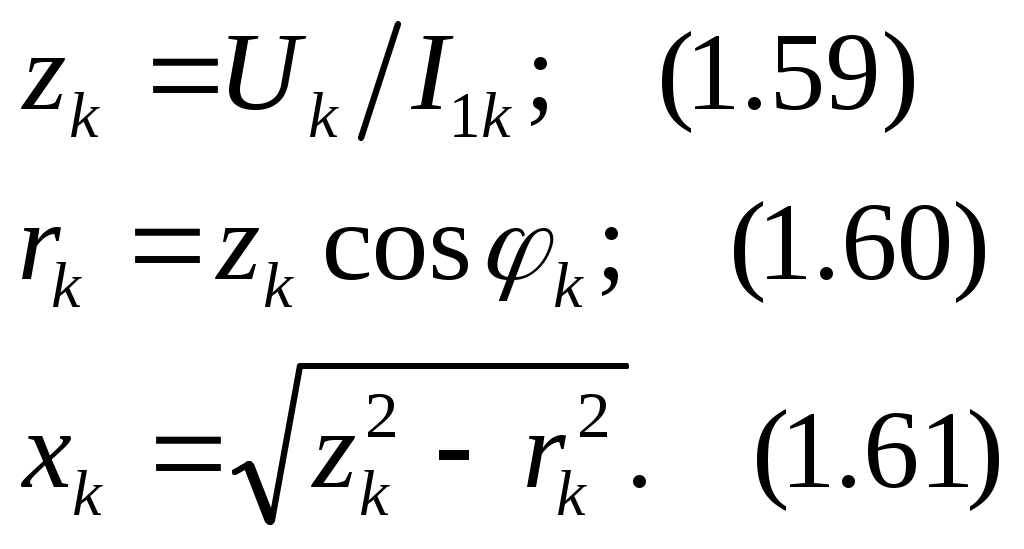





Полученные значения сопротивлений г_к и z_k, мощности Р_к, коэффициента мощности соsφ_к и напряжения к.з. u_к следует привести к рабочей температуре обмоток +75 °С: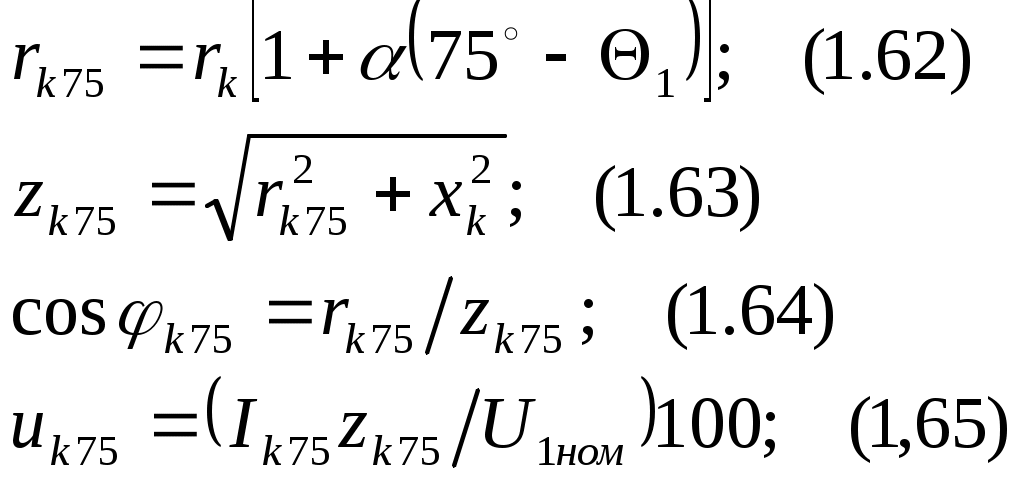





Здесь г_к — активное сопротивление к.з. при температуре θ₁; α = 0,004 —температурный коэффициент для меди и алюминия.

Так как при опыте к.з. основной поток Ф_mах составляет всего лишь несколько процентов по сравнению с его значением при номинальном первичном напряжении, то магнитными потерями, вызываемыми этим потоком, можно пренебречь. Следовательно, можно считать, что мощность Р_k, потребляемая трансформатором ври опыте к.з., идет полностью на покрытие электрических потерь в обмотках трансформатора:



Мощность к.з. приводят к рабочей температуре обмоток +75 °С:



Пример 1.5. Результаты измерений при опыте короткого замыкания трехфазного трансформатора мощностью 100 кВ-А линейными напряжениями (5,3/0,22 в, соединением обмоток Y/Y приведены в табл. 1.1 (напряжение подводилось со стороны ВН). Построить характеристики короткого замыкания: зависимость тока к.з. I_1k, мощности к.з. P_k и коэффициента мощности cosφ_K от напряжения короткого замыкания U_k.

Решение. Ниже приведен расчет значений параметров опыта короткого замыкания, соответствующих номинальному (фазному) напряжению к.з. U_kHOM=190 В, при котором ток к.з. I_k =I_1ном=S_ном/(√3 U₁._HOM)=100/(√3•6,3)=9,15А (измерение 4 в табл. 1.1).

Таблица 1.1

№ измерения	UkA, B	UkB, B	UkC, B	IkA, A	IkB, A	IkC, A	Pk, Bт
1 2 3 4	64 105 147 191	63 105 146 189	62 103 145 190	2,9 5,1 7,2 9,2	3,0 5,0 7,0 9,2	3,1 5,0 7,2 9,1	190 513 1040 1780

Среднее (для трех фаз) значение фазного напряжения к.з. по (1.49)

U_к.ном = (191 +189 +190)/3 = 190 В.

Среднее (для трех фаз) значение тока к.з. по (1.50)

I_1k=(9,2+9,2+9,1)/3=9,15А.

Параметры схемы замещения трансформатора при опыте короткого замыкания: полное сопротивление к.з. по (1.59) z_k=U_к.ном/I_1ном=190/9,15=20,8Ом; из выражения мощности к.з. P_k = I_1k²r_k, определим активное сопротивление к.з.:

r_k = P_k /(3 I₁²_ном)=1780/(3·9,15²) = 7,1 Ом;

индуктивное сопротивление к.з. по (1.61)



Приняв температуру θ₁= 20 °С, полученные значения величин приводим к рабочей температуре обмоток +75 °С: активное сопротивление к. з. по (1.62)

r_k75= 7,1[1 + 0,004(75 - 20)] = 8,6 Ом;

полное сопротивление к.з.



мощность к.з. по (1.64)

Р_k75=3I_1k²r_k75=3·9.15²·8.6 =2160 Вт;

коэффициент мощности по (1.64)

cosφ_k75 = r_k75 /z_k75= 8.6/21.5 = 0,40;

напряжение к.з. по (1.65)

u_k75 =( I_1k z_k.₇₅/U_lмм)100 = (9,15·21,5·√3/6300)l00 = 5,4%.

В таком же порядке рассчитываем параметры опыта к.з. для других значений тока к.з. Результаты расчета заносим в табл. 1.2, а затем строим характеристики короткого замыкания (см. рис. 1.33).

Таблица 1.2

№ измерения	Uк,В	I1k,А	Рk75,ВТ	cosφk75
1 2 3 4	65 108 152 190	3 5 7 9,15	230 620 1260 2160	0,40 0,40 0,40 0,40

§ 1.12. Упрощенная векторная диаграмма трансформатора

Векторная диаграмма нагруженного трансформатора (см. рис. 1.19) наглядно показывает соотношение между параметрами трансформатора. Из-за сложности эта диаграмма не может быть использована для практических расчетов. Для упрощения диаграммы и придания ей практического значения в силовых трансформаторах, работающих с нагрузкой, близкой к номинальной, пренебрегают током х.х. и считают, что 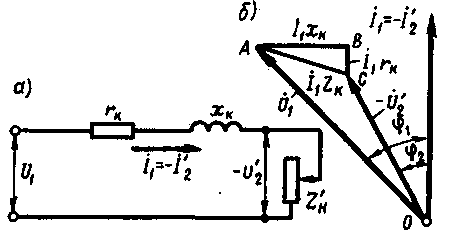. Полученная в этом случае ошибка вполне допустима, так как ток I ₀ по сравнению с токами и невелик (см. § 1.14). При сделанном допущении схема замещения трансформатора приобретает упрощенный вид, так как не имеет ветви намагничивания и состоит только из последовательных участков r_k=r_l+r’₂и х_к = x_l + х'₂ (рис.1.35, а).



Рис. 1.35. Упрощенные схемы замещения (а) и векторная диаграмма (б) трансформатора

Соответственно упрощенной схеме замещения построена и упрошенная векторная диаграмма (рис. 1.35, 6), в которой прямоугольный треугольник ABCпредставляет собой треугольник к.з., стороны которого соответственно равны:

BC = I₁r_k; CA = I₁Z_k; AB= I₁x_K.

Упрощенную векторную диаграмму трансформатора строят по заданным значениям напряжения U_1HOM, тока I_1nom, коэффициента мощности соsφ_2ном и параметрам треугольника к.з. U_K, U_KAи U_к.р.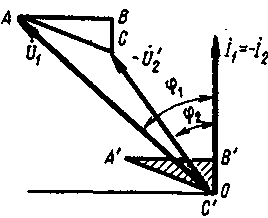



Рис. 1.36. Построение упрощенной векторной диаграммы

Порядок построения упрощенной векторной диаграммы следующий (рис. 1.36). На оси ординат строят вектор тока , затем под углом φ₂ строят вектор напряжения . Треугольник к.з. А'В'С' строят таким образом, чтобы точка С' совместилась с точкой начала координат, а катет С'В' — с осью ординат. Затем этот треугольник переносят, совмещая точку С с концом вектора - , а стороны оставляя параллельными исходному треугольнику А'В'С'. Получают треугольник ABC. После этих построений из начала осей координат (точка О) проводят вектор первичного (фазного) напряжения и определяют угол фазового сдвига φ₁ между первичным током , и первичным напряжением .

§ 1.13. Внешняя характеристика трансформатора

При колебаниях нагрузки трансформатора его вторичное напряжение меняется. В этом можно убедится, воспользовавшись упрощенной схемой замещения трансформатора (см. рис. 1.35.), из которой следует, что

Измерение вторичного напряжения трансформатора при увеличении нагрузки от х.х. до номинальной является важнейшей характеристикой трансформатора и определяется выражением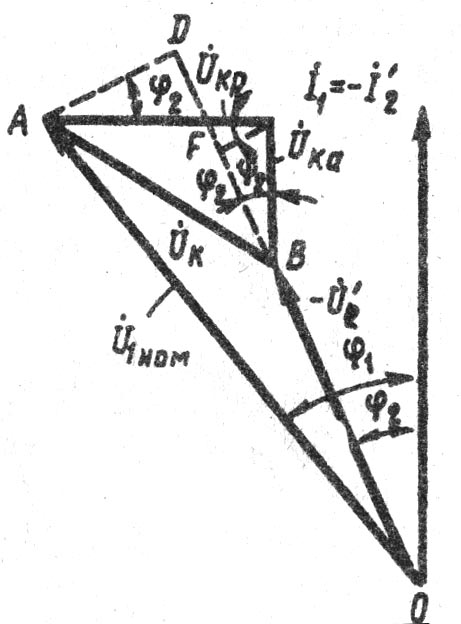

(1.67)



Рис. 1.37. К выводу формулы

Для определения воспользуемся упрощенной векторной диаграммой трансформатора, сделав на ней следующее дополнительное построение (рис. 1.37.). Из точки А отпустим перпендикуляр на продолжение вектора , получим точку D. С некоторым допущением будем считать, что отрезок представляет собой разность , где , тогда

(1.68.)

Измерение вторичного напряжения (1.67) с учетом (1.68) примет вид

(1.69)

Обозначим (U_k.a./U_1ном)100=U_k.a.; (U_k.p./U_1ном)100=U_k.p., тогда выражение изменения вторичного напряжения трансформатора при увеличении нагрузки примет вид

(1.70)

Выражение (1.70) дает возможность определить изменение вторичного напряжения лишь при номинальной нагрузке трансформатора. При необходимости расчета измерение вторичного напряжения для любой нагрузки в выражение (1.70) следует ввести коэффициент нагрузки, представляющий собой относительное значение тока нагрузки =I₂/I_2ном

(1.71)

из выражения (1.71) следует, что изменение вторичного напряжения 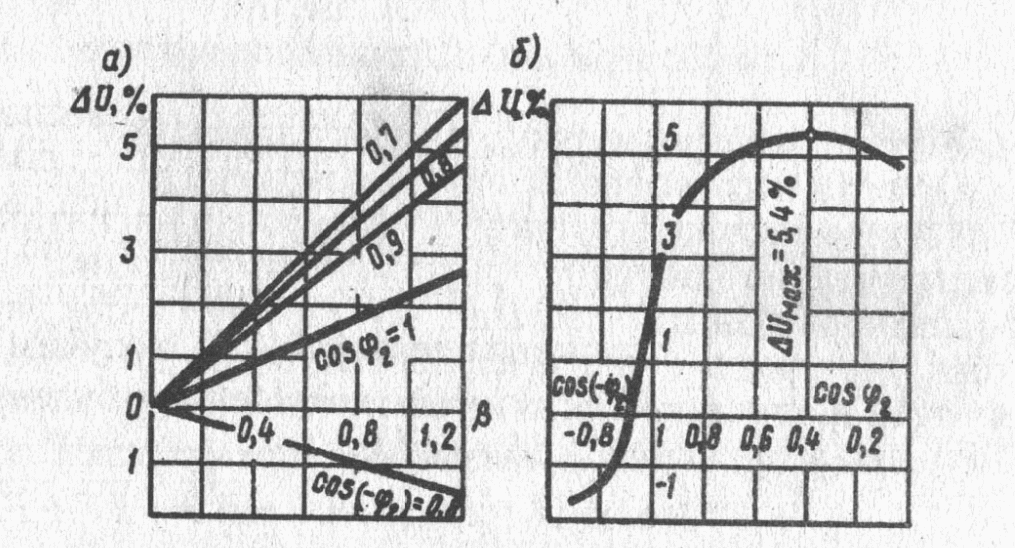зависит не только от величины нагрузки трансформатора (), но и от характера этой нагрузки (₂).



Рис. 1.38. Зависимость от величины нагрузки (а) и коэффициента мощности нагрузки (б) трехфазного трансформатора (100 кВ·А, 6,3/0,22 кВт, u_r=5,4%, cos_r=0,4)
На рис. 1.38, а представлен график зависимости при cos₂=const, а на рис. 1.38, б – график при =const. На этих графиках отрицательные значения при работе трансформатора с емкостной нагрузкой соответствуют повышению напряжения при переходе от режима х.х. к нагрузке. Имея в виду, что получим еще одно выражение для расчета изменения вторичного напряжения при любой нагрузке:

(1.72)

Из (1.72) следует, что наибольшее значение изменения напряжения имеет место при равенстве углов фазового сдвига ₂=_к, тогда cos(_k-₂)=1.

Зависимость вторичного напряжения 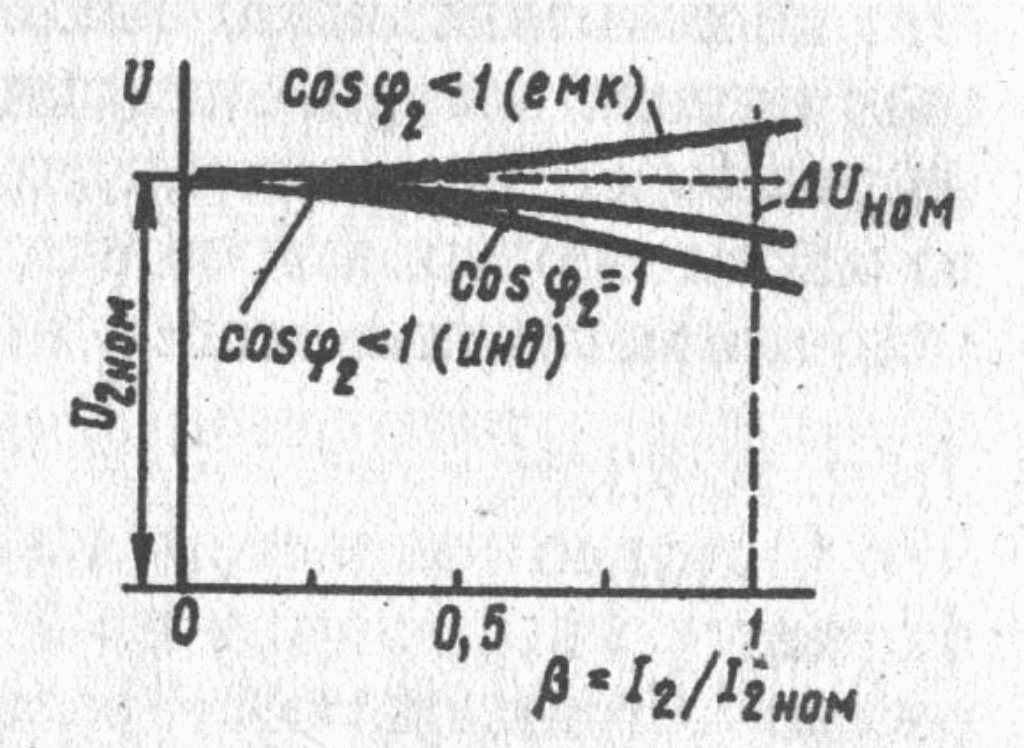трансформатора от нагрузки называют внешней характеристикой. Напомним, что в силовых трансформаторах за номинальное напряжение на зажимах вторичной обмотки в режиме х.х. при номинальном первичном напряжении (см. § 1.3.).



Рис. 1.39. Внешние характеристики трансфоматора.

Вид внешней характеристики (рис. 1.39) зависит от характера нагрузки трансформатора (cos₂). Внешнюю характеристику трансформатора можно построить по (1.72) путем расчета для разных значений  и cos₂.

Пример 1.6. Для трансформатора, данные которого приведены в примерах 1.4 и 1.5, (см. § 1.11.), определить изменение вторичного напряжения при номинальной нагрузке (=1) с коэффициентом мощности cos₂ = 1,8 для нагрузок двух характеров: активно-индуктивной и ативно-емкостной.

Решение. Из примера 1.4 имеем: u_k75 =5,4%; cosφ_k75=0,4; sinφ_k75 =0,92 . По (1.72) при cosφ₂ = 0,8 и sinφ₂ = 0,6 получим:

для активно-индуктивной нагрузки ∆U=5,4(0,4•0,8+0,92•0,6)=4,65%;

для активно-емкостной нагрузки ∆U=5,4[0,4•0,8+0,92•(-0,6)]=-1,2%.

В результате аналогичных расчетов, проделанных при β=0÷1,2, для нагрузок с cosφ₂, равным 0,7; 0,8; 0,9 и 1,0, получены данные, по которым построены графики ∆U = f(β), представленные на рис 1 38, а.

Наибольшее изменение напряжения соответствует активно-индуктивной нагрузке с cosφ₂ = cosφ_k75 = 0,40 и коэффициенту нагрузки β = 1 (перегрузка трансформатора недопустима) ∆U _тax= u_k75= 5,4% (см рис. 1.38,6)