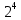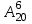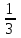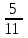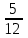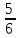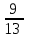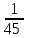1
|
В вазе стоят 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать из неё 6 гвоздик одного цвета.
|
91
|
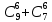
|
|
|
2
|
Сколькими способами можно назначить двух ребят на дежурство по столовой, если в классе
А) 25 человек. Б)24
|
А) 276
Б)300
|
А) (25*24)/2=300
Б) 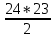 =276 =276
|
|
|
3
|
Сколькими способами 4 различные монеты можно разложить по двум карманам.
|
16
|
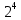
|
|
|
4
|
Сколько различных чётных чисел с неповторяющимися цифрами можно записать. Используя цифры 1;2;3;5.
|
6
|
|
|
|
5
|
Сколько шестизначных чисел можно составить из цифр 0;2;5;6;7;8 (без повторения)
|
600
|
|
|
|
6
|
Учащиеся 9 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 24 учащихся.
|
552
|
23*24
|
|
|
7
|
Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов может он выбрать.
|
5040
|
|
|
|
8
|
Сколькими способами можно выбрать один цветок из корзины, в которой имеется 12 гвоздик, 15 роз и 7 хризантем.
|
34
|
|
|
|
9
|
На плоскости отметили точку. Из неё провели 9 лучей. Сколько получилось при этом углов.
|
36
|
|
|
|
10
|
Сколько существует способов выбрать троих ребят из четверых желающих дежурить по столовой.
|
|
4
|
|
|
|
|
|
|
|
11
|
Сколькими способами 6 студентов, сдающих экзамен, могут занять места в аудитории, в которой стоит 20 одноместных столов.
|
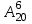
|
|
|
|
12
|
Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать.
|
870
|
|
|
|
13
|
Сколькими способами 3 награды (за 1,2 и 3 места) могут быть распределены между 10 участниками соревнований.
|
120
|
|
|
|
14
|
В цветочном киоске 7 видов цветов. Сколькими разными способами можно составить букет, содержащий 3 цветка.
|
|
84
|
|
|
|
|
|
|
|
15
|
Сколькими способами можно составить трёхцветный флаг, если имеется материя 5 различных цветов.
|
60
|
|
|
|
16
|
Сколько различных трёхзначных чисел можно составить из цифр 1;2;3;4;5 при условии, что каждая цифра встречается один раз.
|
120
|
|
|
|
17
|
Сколько различных шестизначных чисел, начинающихся цифрой 2 и оканчивающихся цифрой 5. можно составить из цифр 1;2;3;4;5;6 при условии, что каждая цифра встречается один раз.
|
|
24
|
|
|
|
|
|
|
|
18
|
На полке лежат 6 маркированных и 3 немаркированных конверта. Наудачу берут 2 конверта. Какова вероятность, что оба конверта маркированные.
|
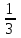
|
|
|
|
19
|
В ящике 5 новых и 6 старых инструментов. Рабочему сразу выдали 3 инструмента. Какова вероятность того, что рабочему выдали только новые инструменты.
|
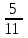
|
|
|
|
|
|
|
|
|
|
|
|
|
20
|
На полке лежат 6 маркированных и 3 немаркированных конверта. Наудачу берут 2 конверта. Какова вероятность, что оба конверта немаркированные.
|

|
|
|
|
21
|
В коробке 8 красных и 4 синих карандаша. Наугад вынимают 5 карандашей. Какова вероятность того, что 3 из них окажутся красными, а 2 синими.
|
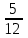
|
|
|
|
|
|
|
|
|
|
|
|
|
22
|
В магазин поступило 30 холодильников, 5 из них имеют заводской дефект. Случайным образом выбирается один холодильник. Какова вероятность того, что он без дефекта.
|
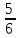
|
|
|
|
23
|
В урне 3 белых, 6 чёрных и 5 синих шаров. Из неё вынимают наудачу 2 шара. Какова вероятность того, что они окажутся разного цвета.
|
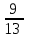
|
|
|
|
|
|
|
|
|
|
|
|
|
24
|
Какова вероятность того, что наудачу выбранное двузначное число простое и сумма его цифр равна 5.
|
|
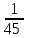
|
|
|
|
|
|
|
|
 Скачать 169.58 Kb.
Скачать 169.58 Kb.
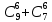
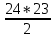 =276
=276