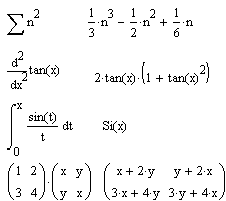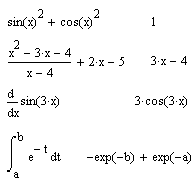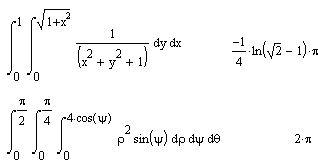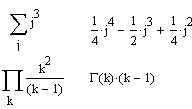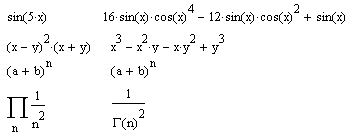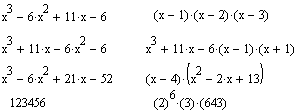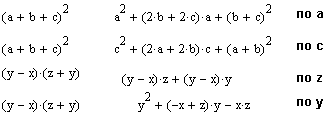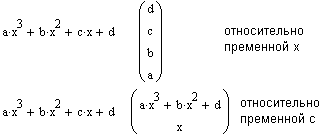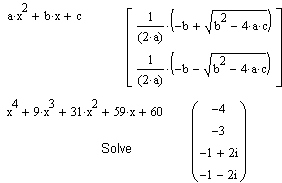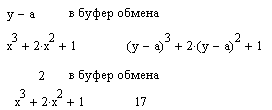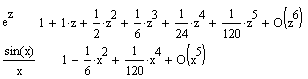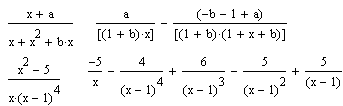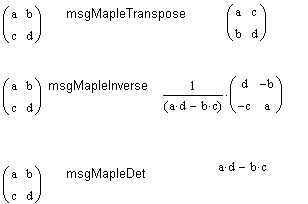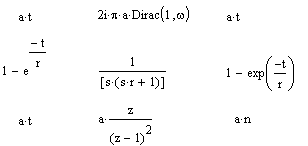Лабы и лекции по Mathcad. 1. 1 Интерфейс пользователя
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
4.1 Возможности символьного процессора MathCAD.Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, разумеется, если такое решение существует в принципе (что бывает далеко не всегда). Ядро символьного процессора системы MathCAD — несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software, у которой MathSoft (разработчик MathCAD) приобрела лицензию на его применение, благодаря чему MathCAD стала (начиная с версии 3.0) системой символьной математики. Прямой доступ к большинству операций ядра (возможный в системе Maple V R5/R6), для пользователя MathCAD, к сожалению, закрыт. К примеру, библиотечный модуль Maple V содержит около 100 функций линейной алгебры, тогда как в модуле MathCAD было только три важнейшие функции из этого раздела. Многие функции и правила преобразования в ядре используются лишь для получения промежуточных преобразований. Тем не менее это обстоятельство нельзя считать уж слишком большим недостатком системы MathCAD. Во-первых, потому, что ее назначение иное — прежде всего решение задач в численном виде, а во-вторых, потому, что система Maple V явно избыточна (в ее ядре около 2800 функций и правил преобразования) и ориентирована на пользователей с весьма далекими от средних потребностями в решении задач компьютерной алгебры (символьной математики) Введение в систему MathCAD символьных вычислений придает ей качественно новые возможности, которые отсутствовали у прежних версий системы. Куда важней, что символьные вычисления выполняются в конечном счете столь же просто (для пользователя), как, скажем, вычисление квадрата х. Символьные вычисления в MathCAD могут быть реализованы тремя способами:
4.2 Команды меню Symbolics.
Само выражение в таком случае не выделяется: ведь и так ясно, что если маркер ввода выделяет переменную какого-либо выражения, то это выражение уже отмечено наличием в нем выделяемой переменной. Следует отметить некоторые особенности при работе с командами меню Symbolics .
Символьные операции разбиты на четыре характерных раздела. Первыми идут наиболее часто используемые операции. Они могут выполняться с выражениями, содержащими комплексные числа или имеющими решения в комплексном виде.
К операциям с выделенными выражениями относятся следующие:
Evaluate (Вычислить) Эта операция содержит подменю со следующими командами:
Команда Evaluate Symbolically тут наиболее важная. Назначение других команд очевидно: они нужны, если результат требуется получить в форме комплексного или действительного числа. К примеру, если вы хотите вместо числа p получить 3.141..., используйте команду Floating Point Evaluation. В режиме символьных вычислений результат может превосходить машинную бесконечность системы. При этом число точных значащих цифр результата практически не ограничено (или, точнее говоря, зависит от емкости ОЗУ). Символьная операция Evaluate Symbolically [Shift+F9] (Вычислить) обеспечивает работу с математическими выражениями, содержащими встроенные в систему функции и представленными в различном виде: полиномиальном, дробно-рациональном, в виде сумм и произведений, производных и интегралов и т. д. Операция стремится произвести все возможные численные вычисления и представить выражение в наиболее простом виде. Она возможна над матрицами с символьными элементами. Производные и определенные интегралы, символьные значения которых вычисляются, должны быть представлены в своей естественной форме. Особо следует отметить возможность выполнения численных вычислений с повышенной точностью — 20 знаков после запятой. Для перехода в такой режим вычислений нужно числовые константы в вычисляемых объектах задавать с обязательным указанием десятичной точки, например 10.0 или 3.0, а не 10 или 3. Этот признак является указанием на проведение вычислений такого типа. На рисунке ниже показаны типовые примеры действия операции Evaluate Symbolically.
Операция Evaluate Symbolically одна из самых мощных. Как видно на рисунка, она позволяет в символьном виде вычислять суммы (и произведения) рядов, производные и неопределенные интегралы, выполнять символьные и численные операции с матрицами. Simplify(Упростить) Символьная операция Simplify (Упростить) — одна из самых важных. Эта операция позволяет упрощать математические выражения, содержащие алгебраические и тригонометрические функции, а также выражения со степенными многочленами (полиномами). Упрощение означает замену более сложных фрагментов выражений на более простые. Приоритет тут отдается простоте функций. К примеру, функция tan(x) считается более сложной, чем функции sin(x) и cos(x). Поэтому tan(x) упрощается так, что получает представление через соотношение этих функций, что несколько неожиданно, так как в некоторых пакетах символьной математики, например Derive, ситуация иная: они заменяют отношение sin(x)/cos(x) функцией tan(x).
Система MathCAD содержит встроенную функцию для вычисления значений определенных интегралов приближенным численным методом. Ею целесообразно пользоваться, когда нужно просто получить значение определенного интеграла в виде числа.
Приведенные примеры могут создать впечатление, что MathCAD лихо справляется со всеми производными, интегралами, суммами и произведениями с помощью операции Simplify. К сожалению, это далеко не так . Нередко система не справляется с кажущимися простыми справочными примерами. Надо помнить, что символьный процессор системы MathCAD обладает заметно урезанной библиотекой функций и преобразований (в сравнении с библиотекой системы Maple V). Поэтому часто система не находит решение в замкнутом виде, хотя оно и приводится в справочнике. Тогда система повторяет введенное выражение или сообщает об ошибке. В результате преобразований могут появляться специальные функции — как встроенные в систему (функции Бесселя, гамма-функция, интеграл вероятности и др.), так и ряд функций, дополнительно определенных при загрузке символьного процессора (интегральные синус и косинус, интегралы Френеля, эллиптические интегралы и др.). Последние нельзя использовать при создании математических выражений. Expand (Разложить по степеням) Действие операции Expand (Разложить по степеням) в известном смысле противоположно действию операции Simplify. Подвергаемое преобразованию выражение расширяется с использованием известных (и введенных в символьное ядро) соотношений, например алгебраических разложений многочленов, произведений углов и т. д. Разумеется, расширение происходит только в том случае, когда его результат однозначно возможен. Иначе нельзя считать, что действие этой операции противоположно действию операции Simplify. К примеру, операция Simplify преобразует сумму квадратов синуса и косинуса в 1, тогда как обратное преобразование многозначно и потому в общем виде невыполнимо.
Последний пример на этом рисунке показывает, что результатом операции может быть специальная математическая функция, которая считается более сложным выражением, чем порождающее ее выражение. С виду, однако, выражения со специальными математическими функциями обычно выглядят гораздо проще, чем исходные выражения. Factor (Разложить на множители) Операция Factor Expression (Разложить на множители) используется для факторизации — разложения выражений или чисел на простые множители. Она способствует выявлению математической сущности выражений; к примеру, наглядно выявляет представление полинома через его действительные корни, а в том случае, когда разложение части полинома содержит комплексно-сопряженные корни, порождающее их выражение представляется квадратичным трехчленом. Примеры действия этой операции даны на рисунке ниже.
Collect (Разложить по подвыражению) Операция Collect(Разложить по подвыражению) обеспечивает замену указанного выражения выражением, скомплектованным по базису указанной переменной, если такое представление возможно. В противном случае появляется окно с сообщением о невозможности комплектования по указанному базису.
В том случае, когда комплектование по базису указанной переменной невозможно, система выдает сообщение об этом. Оно выводится в отдельном небольшом информационном окошке. Polynomial Coefficients( Полиномиальные коэффициенты) Операция Polynomial Coefficients(Полиномиальные коэффициенты) в ранних версиях MathCAD отсутствующая, служит для вычисления коэффициентов полинома.
Следующая группа символьных операций выполняется с выражениями, требующими указания переменной, по отношению к которой выполняется операция. Для этого достаточно установить на переменной курсор ввода. Само выражение при этом не указывается отдельно, поскольку указание в нем на переменную является одновременно и указанием на само выражение. Если выражение содержит другие переменные, то они рассматриваются как константы. К числу операций с выделенными переменными относятся:
Ранее отмечалось, что усложнение уравнения, например переход от квадратного уравнения к кубическому, может вызвать и существенное усложнение результата. Тогда система представляет решение в более компактном виде (но без общепринятой математической символики) и предлагает занести его в буфер обмена. С помощью операции Paste<(Вставить) в позиции Edit (Правка) главного меню можно перенести решение в основное окно системы, но оно имеет уже тип текстового комментария, а не математического выражения, пригодного для дальнейших преобразований. Впрочем, часть его можно (опять-таки с помощью буфера обмена) ввести в формульные блоки для последующих преобразований и вычислений. Более того, форма представления результата в таком случае отличается от принятой в системе MathCAD (например, в качестве знака деления используется косая черта, для возведения в степень — составной знак ** и т. д.). Это сделано ради компактности представления результатов вычислений. В случаях, описанных выше, пользователю надо реально оценить свои силы в упрощении решения. Это придется сделать вручную. При технических расчетах специалист нередко знает, какие из параметров решения несущественны и может отбросить их. Однако для строгих математических расчетов это не всегда возможно, поэтому даже громоздкий результат может быть весьма полезным с познавательной точки зрения. Substitute (Заменить переменную) Операция Substitute(Подстановка) возвращает новое выражение, полученное путем подстановки на место указанной переменной некоторого другого выражения. Последнее должно быть подготовлено и скопировано (операциями Cutили Copy)в буфер обмена. Наряду с получением результата в символьном виде эта команда позволяет найти и числовые значения функции некоторой переменной путем замены ее на числовое значение.
Differentiate(Дифференцировать переменной) Нахождение символьного значения производной — одна из самых распространенных задач в аналитических вычислениях. Операция Differentiate (Дифференцировать по переменной) возвращает символьное значение производной выражения по той переменной, которая указана курсором. Для вычисления производных высшего порядка (свыше 1) нужно повторить вычисление необходимое число раз. На рисунке ниже показано применение операции дифференцирования. 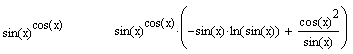 Integrate (Интегрировать по переменной) Другая не менее важная операция при символьных вычислениях — вычисление интегралов (или нахождение первообразных) для аналитически заданной функции. Для этого используется операция Integrate (Интегрировать по переменной). Она возвращает символьное значение неопределенного интеграла по указанной курсором ввода переменной. Выражение, в состав которого входит переменная, является подынтегральной функцией. 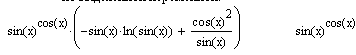 На рисунке показаны пример символьного интегрирования по переменной х. Визуализация таких вычислений (как и описанных выше), прямо скажем, не велика: совсем неясно, откуда берутся выражения в документе и результаты чего они представляют. Как и для операции дифференцирования, в состав исходных выражений и результатов символьного интегрирования могут входить встроенные в систему специальные математические функции. Expand to Series... (Разложить в ряд) Операция Expand to Series...(Разложить в ряд) возвращает разложение в ряд Тейлора выражения относительно выделенной переменной с заданным по запросу числом членов ряда п (число определяется по степеням ряда). По умолчанию задано n=6.<\p>
Символьные операции нередко можно комбинировать для решения сложных задач. Convert to Partial Fraction (Разложить на элементарные дроби) Операция Convert to Partial Fraction(Разложить на элементарные дроби) возвращает символьное разложение выражения, представленное относительно заданной переменной в виде суммы правильных целых дробей.
Операции с выделенными матрицами представлены позицией подменю Matrix (Матричные операции), которая имеет свое подменю со следующими операциями:
В MathCAD 2000 PRO в позиции Symbol содержится раздел операций преобразования, создающий подменю со следующими возможностями: Fourier Transform (Преобразование Фурье)— выполнить прямое преобразование Фурье относительно выделенной переменной; Inverse Fourier Transform (Обратное преобразование Фурье) — выполнить обратное преобразование Фурье относительно выделенной переменной; Laplace Transform (Преобразование Лапласа)— выполнить прямое преобразование Лапласа относительно выделенной переменной (результат — функция от переменной s), Inverse Laplace Transform (Обратное преобразование Лапласа) — выполнить обратное преобразование Лапласа относительно выделенной переменной (результат — функция от переменной t); Z Transform (Z-преобразование) — выполнить прямое Z-преобразование выражения относительно выделенной переменной (результат — функция от переменной z); Inverse Z Transform (Обратное Z-преобразование) - выполнить обратное Z-преобразование относительно выделенной переменной (результат — функция от переменной n).
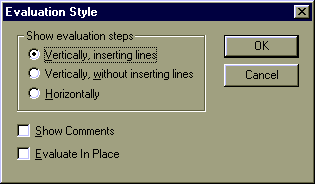
В меню Symbolics находится команда Evaluation Style..., при исполнении которой на экран выводится диалоговое окно, позволяющее установить вид вывода результатов при работе с символьным процнссором MathCAD.
|