тригонометрические функции. КАРАГАНДИНСКИЙ УНИВЕРСИТЕТ БУКЕТОВА. "Тригонометрические и обратно тригонометрические функции"

• Название: "Тригонометрические и обратно тригонометрические функции"
• Анкор: тригонометрические функции
• Дата: 25.11.2022
• Размер: 242.49 Kb.
• Имя файла: КАРАГАНДИНСКИЙ УНИВЕРСИТЕТ БУКЕТОВА.docx
• Тип: Реферат; #812361

КАРАГАНДИНСКИЙ УНИВЕРСИТЕТ БУКЕТОВА

КАФЕДРЫ ФИЗИКИ И НАНОТЕХНОЛОГИЙ

РЕФЕРАТ

На тему : “Тригонометрические и обратно тригонометрические функции”

РАБОТУ ВЫПОЛНИЛА:

Маратова Дильнур Жасланкызы

Студент 2 курса

Группа ФЕР 203

г. Караганда

Оглавление

Введение

1. Общие вопросы изучения тригонометрических функций в школе.

2. Теория обратных функций. Обратные тригонометрические функции

2.1.Определение обратной функции

2.2.Определение, свойства и графики обратных тригонометрических

Функций

3.3. Заключение

Введение

Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода, а ведь их решение систематизирует знания учащихся по всему курсу тригонометрии, проверяет понимание и усвоение важнейших понятий раздела.Исходя из вышесказанного, проблема исследования сформулирована следующим образом: в чем заключается основная сложность при обучении решению уравнений и неравенств, содержащих обратные тригонометрические функции. Это проблема и обусловила тему исследования: «Обратные тригонометрические функции».

Объект исследования - обратные тригонометрические функции.

Предмет исследования - изучение теории обратных тригонометрических функции, различных методов и приемов решения уравнений и неравенств, содержащих обратные тригонометрические функции.

Цель исследования состоит в том, чтобы на основе изучения научной, учебной и периодической литературы по рассматриваемому вопросу систематизировать и последовательно изложить теоретический материал с подробным разбором упражнений по данной теме.

1. 
   Общие вопросы изучения тригонометрических функций
   

в школьном курсе

Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника, является разделом геометрии, тригонометрические функции являются объектом изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.

Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и являются тригонометрическими функциями, встречаются уже в Ш в. до н. э. в работах Евклида, Архимеда, Аполлония Пергского и др. Тригонометрия от греческих: trigonom – “треугольник”, metreo – “измеряю”, изучает зависимость между сторонами и углами треугольника.

Тригонометрия возникла из пратических нужд человека. С ее помощью можно определить расстояния до недоступных предметов. Она существенно упрощает процесс геодезической съемки местности, нужный для составления карт.

Зачатки тригонометрических познаний родились в древности. Жрецы постоянно наблюдали за небом, за перемещением звезд. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вспомогательным разделом.

Во введении говорилось о необходимости изучения тригонометрических функций числового аргумента в школьном курсе алгебре и математического анализа. Что же обуславливает данную необходимость?

Итак, основными целями изучения тригонометрических функций числового аргумента являются:

1.Ознакомление учащихся с новым видом трансцендентных функций;

2.Развитие навыков вычислительной практики (работа с трансцендентными функциями зачастую требует громоздких вычислений);

3.Наглядная иллюстрация всех основных свойств функций (в особенности периодичности);

4.Установление межпредметных связей с практикой (изучение колебаний маятника, электрического тока, волновой теории света невозможны без знаний о тригонометрических функциях);

5.Развитие логического мышления (обилие формул порождает необходимость преобразований не алгебраического характера, которые носят исследовательский характер).

В изучении тригонометрических функций можно выделить следующие этапы:

1.Первое знакомство с тригонометрическими функциями углового аргумента в геометрии. Значение аргумента рассматривается в промежутке (0^о;90^о). На этом этапе учащиеся узнают, что sin, сos, tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения.

2.Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0^о;180^о). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.

3.Введение понятий тригонометрических функций числового аргумента.

4.Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе и с помощью производной.

Отметим, что существует несколько способов определения тригонометрических функций. Их можно подразделить на две группы: аналитические и геометрические. К аналитическим способам относят определение функции у = sin х как решения дифференциального уравнения

f ^''(х)=-c*f(х) или как сумму степенного ряда sin х = х – х³ /3!+ х⁵ /5! – …

К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности. В школьном курсе предпочтение отдается геометрическим способам в силу их простоты и наглядности.

Отметим, что изучение тригонометрических функций в школьном курсе имеет некоторые особенности. Во-первых, до изучения тригонометрических функций, рассматривались функции вида у=f(x), где х и у – некоторые действительные числа, здесь же - углу ставится в соответствие число, что является несколько непривычным для учащихся. Кроме того, раньше все функции задавались формулами, в которых явным образом был указан порядок действий над значениями аргумента для получения значений функции. Теперь же учащиеся сталкиваются с функциями, заданными таблично.

Таким образом, изучая тригонометрические функции, учащиеся лучше начинают разбираться в сущности самого понятия функции. Они начинают осознавать, что функцией может быть зависимость между любыми множествами объектов, даже если они имеют различную природу (лишь бы каждому значению аргумента соответствовало единственное значение функции).

2.Теория обратных функций

Обратные тригонометрические функции

Определение обратной функции

Определение. Если функция f(x) задает взаимно однозначное соответствие между своей областью определения X и своей областью значений У (иными словами, если любым различным значениям аргумента соответствуют различные значения функции), то говорят, что функция f(x) имеет обратную функцию или что функция f(x) обратима.

Определение. Обратная функция - это правило, которое каждому числу у є У сопоставляет число х є X, причем y=f(x). Область определения обратной функции есть множество У, область значений - X.

Теорема о корне . Пусть функция f возрастает (или убывает) на промежутке I, число а - любое из значений, принимаемых f на этом промежутке. Тогда уравнение f(x)=a имеет единственный корень в промежутке I.

Доказательство. Рассмотрим возрастающую функцию f (в случае убывающей функции рассуждения аналогичны). По условию в промежутке I существует такое число b, что f(b)=a. Покажем, что b - единственный корень уравнения f(x)=a.

Допустим, что на промежутке I есть еще число с≠ Ь, такое что f(c)=a. Тогда или сb. Но функция f возрастает на промежутке I, поэтому соответственно либо f(c)f(b). Это противоречит равенству f(c)= f(b)=a. Следовательно, сделанное предположение неверно и в промежутке I, кроме числа b, других корней уравнения f(x)=a нет.

Теорема об обратной функции. Если функция f возрастает (или убывает) на промежутке I, то она обратима. Обратная к f функция g, определенная в области значений f также является возрастающей (соответственно убывающей).

Доказательство. Положим для определенности, что функция f возрастает. Обратимость функции f - очевидное следствие теоремы о корне. Поэтому остается доказать, что функция g, обратная к f, возрастает на множестве E(f).

Пусть х1 и х2 - произвольные значения из E(f), такие, что х2> х1 и пусть y1= g (х1), у2= g(х2). По определению обратной функции х1= f(y1) и х2= f(y2).

Воспользовавшись тем условием, что f - возрастающая функция, находим, что допущение y1≥ y2 приводит к выводу f(y1) > f(y2), то есть х1 > х2 . Это

противоречит предположению х2> х1 Поэтому, y1 > y2 , то есть из условия х2> х1 следует, что g(x2)> g(х1). Что и требовалось доказать.

Исходная функция и обратная ей являются взаимно обратными.

Графики взаимно обратных функций

Теорема. Графики взаимно обратных функций симметричны относительно прямой у=х.

Доказательство. Заметим, что по графику функции f можно найти числовое значение обратной к f функции g в произвольной точке а. Для этого нужно взять точку с координатой а не на горизонтальной оси (как это обычно делается), а на вертикальной. Из определения обратной функции следует, что значение g(a) равно b.

Таким образом, если считать, что выбрана несколько необычная система координат, то можно сказать, что график обратной к f функции g - это график функции f (построенной в обычной системе координат).

Для того, чтобы изобразить график g в привычной системе координат, надо отразить график f относительно прямой у=х.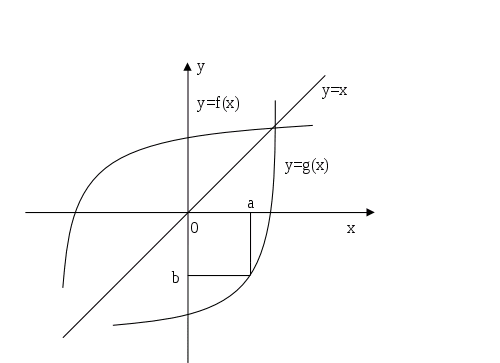



Алгоритм составления обратной функции для функции y=f(x), x  X.

1 .Убедиться в том, что функция y=f(x) обратима на X.

2.Из уравнения y=f(x) х выразить через у, учитывая при этом, что х є X.

З.В полученном равенстве поменять местами х и у.

2.2.Определение, свойства и графики обратных тригонометрических

функций

Арксинус

Функция синус возрастает на отрезке   и принимает все значения от -1 до 1. Следовательно, по теореме о корне для любого числа а, такого, что  , в промежутке   существует единственный корень уравнения sin x = a. Это число и называют арксинусом числа а и обозначают arcsin а.

Определение.Арксинусом числа а, где  , называется такое число из отрезка , синус которого равен а.

Свойства.

1. 
   D(у) = [ -1;1 ]
   
2. 
   Е(у) = [-π/2;π/2]
   
3. 
   у (-х) = arcsin(-х) = - arcsin х – функция нечетная, график симметричен относительно точки О(0;0).
   
4. 
   arcsin х = 0 при х = 0.
   
5. 
   arcsin х > 0 при х є (0;1]
   

arcsin х < 0 при х є [-1;0)

6. 
   у = arcsin х возрастает при любом х є [-1;1]
   

-1 ≤ х₁ < х₂ ≤ 1 <=> arcsin х₁ < arcsin х₂ – функция возрастающая.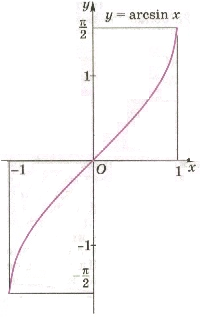



Арккосинус

Функция косинус убывает на отрезке [0; ] и принимает все значения от -1 до 1. Поэтому для любого числа а, такого, что |а|1, на отрезке [0; ] существует единственный корень в уравнении cosx=a. Это число в называют арккосинусом числа а и обозначают arcos а.

Определение.Арккосинусом числа а, где -1 а 1, называется такое число из отрезка [0; ], косинус которого равен а.

Свойства.

1. 
   D(у) = [-1;1]
   
2. 
   Е(у) = [0;π]
   
3. 
   у(-х) = arccos(-х) = π - arccos х – функция не является ни четной, ни нечетной.
   
4. 
   arccos х = 0 при х = 1
   
5. 
   arccos х > 0 при х є [-1;1)
   

arccos х < 0 – нет решений

6. 
   у = arccos х убывает при любом х є [-1;1]
   

-1 ≤ х₁ < х₂ ≤ 1 <=> arcsin х₁ ≥ arcsin х₂ – убывающая.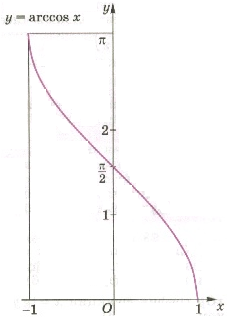



Арктангенс

Функция тангенс возрастает на отрезке - , следовательно, по теореме о корне уравнение tgx=a, где а - любое действительное число, имеет единственный корень х на интервале - . Этот корень называют арктангенсом числа а и обозначают arctga.

Определение.Арктангенсом числа a R называется такое число х ,<sup>тангенс которого равен а.

Свойства.</sup>

1. 
   D(у) = R
   
2. 
   Е(у) = (-π/2;π/2)
   
3. 
   у(-х) = у = arctg(-х) = - arctg х – функция является нечетной, график симметричен относительно точки О(0;0).
   
4. 
   arctg х = 0 при х = 0
   
5. 
   Функция возрастает при любом х є R
   

-∞ < х₁ < х₂ < +∞ <=> arctg х₁< arctg х₂

6. 
   Функция непрерывна при любом х є R.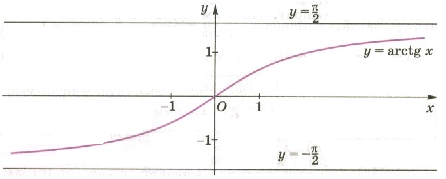
   

Арккотангенс

Функция котангенс на интервале (0; ) убывает и принимает все значения из R. Поэтому для любого числа а в интервале (0; ) существует единственный корень уравнения ctg х = а. Это число а называют арккотангенсом числа а и обозначают arcctg а.

Определение. Арккотангенсом числа а, где а   R, называется такое число из интервала (0; ), котангенс которого равен а.

Свойства.

1. 
   D(у) = R
   
2. 
   Е(у) = (0;π)
   
3. 
   у(-х) = arcctg(-х) = π - arcctg х – функция не является ни четной, ни нечетной.
   
4. 
   arcctg х = 0 – не существует.
   
5. 
   Функция у = arcctg х убывает при любом х є R
   

-∞ < х₁ < х₂ < + ∞ <=> arcctg х₁ > arcctg х₂

6. 
   Функция непрерывна при любом х є R.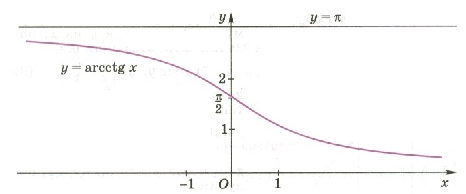
   

Заключение.

Изучив литературу по выбранной теме, я узнала очень много интересных фактов из истории развития тригонометрии как науки, узнала очень много до сих пор не известных мне имён математиков прошлого.

Я повторила решение тригонометрических уравнений школьного курса алгебры и научилась решать уравнения методом введения вспомогательного угла – такие уравнения встречаются в сборнике для проведения итоговой аттестации выпускников.