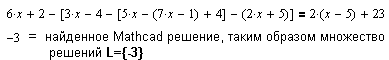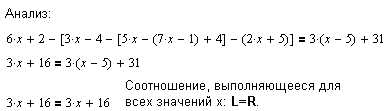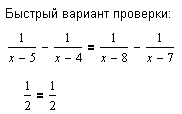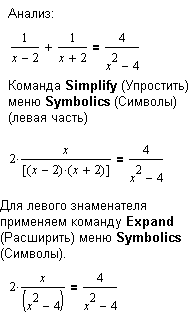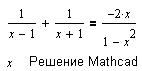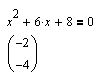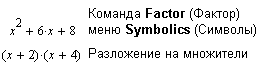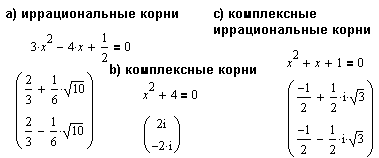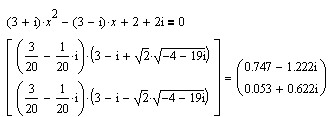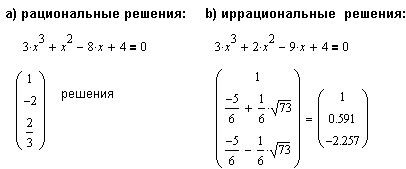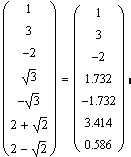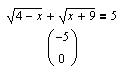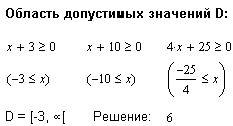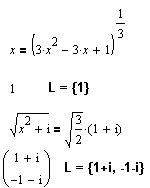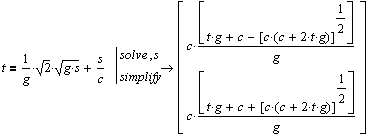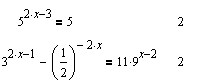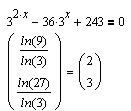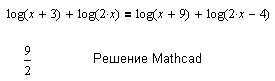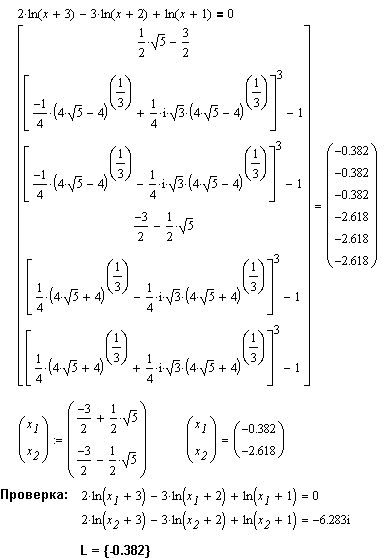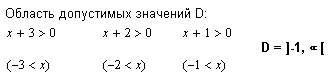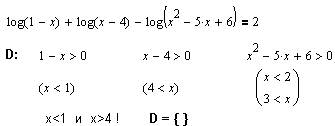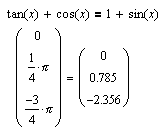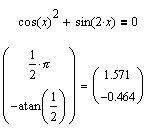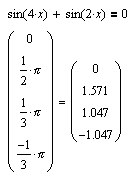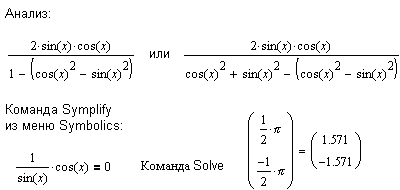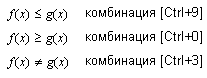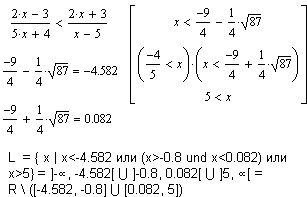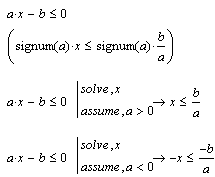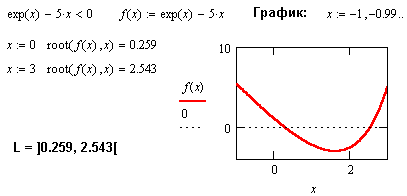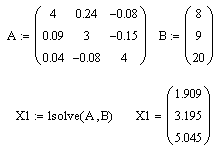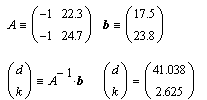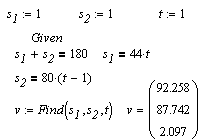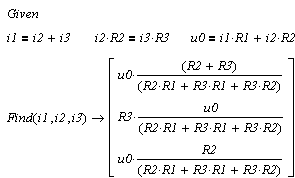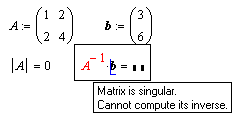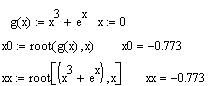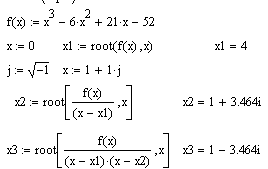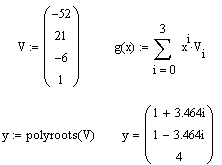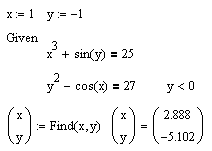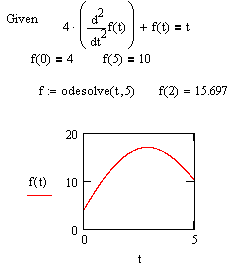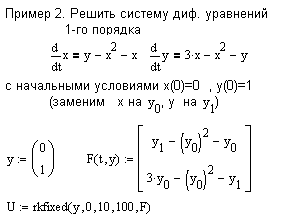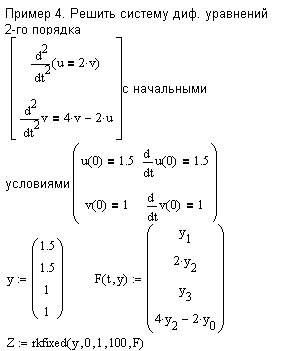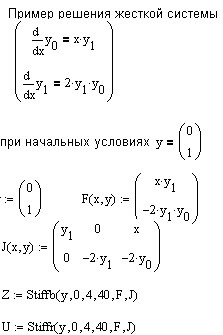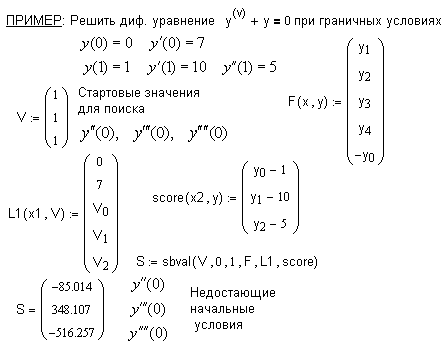4.4 Оптимизация.
Оптимизация вычислений достигается заменой сложной функции или математиского выражения их аналитическим представлением (если оно, конечно, есть). Для включения процесса оптимизации необходимо выделить выражение, которое хотелось бы оптимизоровать, и выполнить команду Optimize позиции главного меню Math.

|
Признаком оптимизации выражения является появление после него красной звездочки. Кроме того, щелкнув правой кнопкой мыши и выбрав из контекстного меню команду Show Popup, можно наблюдать появление окна с оптимизированным выражением.
|
Особый выигрыш оптимизация может дать при многократном вычислении сложных функций, содержащих интегралы, производные, суммы, произведения и ряды.
Лекция 5.
Решение уравнений и систем.
5.1 Решение алгебраических (и других) уравнений и систем.
5.2 Решение дифференциальных уравнений и систем (задача Коши и граничные задачи).
5.3 Задание.

   
5.1 Решение алгебраических (и других) уравнений и систем.
Линейные алгебраические уравнения.
Квадратные уравнения и алгебраические уравнения высших порядков.
Иррациональное уравнения.
Экспоненциальные и логарифмические уравнения.
Тригонометрические уравнения.
Неравенства.
Системы линейных уравнений.
Нелинейные уравнения и системы уравнений.

| Линейные алгебраические уравнения. |
Определение: Уравнение вида ax+b=0 с заданным базовым множеством Gx, a из Ga , b из Gb называется линейным уравнением.
Этапы решения при помощи Mathcad:
Ввести уравнение (знак "=" вводится при помощи комбинации [Ctrl++]).
Выделить курсором переменную, относительно которой должно быть решено уравнение.
Выбрать команду Solve (Вычислить) подменю Variable (Переменные) меню Symbolics (Символы).
При решении линейных уравнений (без параметров) или дробных уравнений, которые сводятся к линейным, MathCAD находит все существующие решения. Однако при этом следует правильно интерпретировать сообщения, выдаваемые системой.
Нормальный случай.
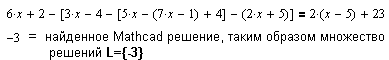
|
В качестве решения MathCAD выдает число - это означает,
|
что уравнение однозначно разрешимо (однозначное решение линейного уравнения над множеством действительных чисел, которое одновременно является областью определения этого уравнения).
Решение отсутствует.
Рассмотрим другой пример: 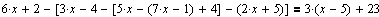

|
После выполнения описанных выше действий для нахождения решения Mathcad выдает сообщение о том, что решение не найдено.
|
Проанализировав данное уравнение приходим к выводу, что выданное Mathcad сообщение означает, что решений нет L={}.
MathCAD выдает сообщение "Решение не найдено", даже если уравнение имеет "формальное решение", которое не принадлежит области определения (смотри примеры ниже).
Многозначность.
Если в качестве решения MathCAD выдает имя переменной, это означает, что множество решений уравнения совпадает с областью определения. Однако, такие понятия, как множество решений уравнения и область определения, отсутствуют в MAthCAD и он не выписывает оболасть определения. Вы можете найти область определения, решая с помощью Mathcad систему неравенств или уравнений
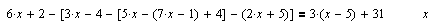 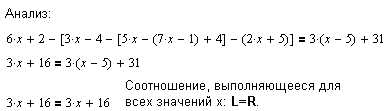
|
Такой результат, выданный Mathcad после выполнения действий по решению уравнения, означает, что любое значение x из базового множества удовлетворяет этому уравнению, т. е. L=R.
|
Дробные уравнения
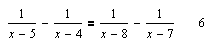
|
Команда Solve (Вычислить) из подменю Variable (Переменные) меню Symbolics (Символы)выдает множество решений: L = {6}.
|
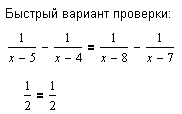
|
Решение 6 копируем в буфер, а затем выделяем маркером переменную x и активизируем команду Substitute (Замена) подменю Variable (Переменные) меню Symbolics (Символы) для замены переменной значением 6.
|
Рассмотрим другой пример: 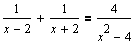
Последнее уравнение (рисунок справа) условно эквивалентно уравнению:2x=4. Решение уравнения Mathcad: 2. Формальное решение x = 2 не входит в область допустимых значений. Mathcad выдает правильное сообщение!
|
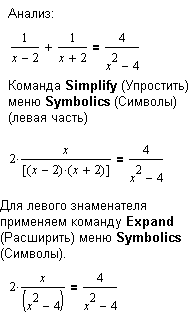
|
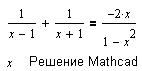
|
Здесь также правильное решение: множество решений совпадает с областью допустимых значений L = D. Только следует учесть, что D={R\{-1,1}}.
|

| Квадратные уравнения и алгебраические уравнения высших порядков. |
Определение: Уравнение P(x)=0 называется алгебраическим уравнением n-го порядка, если P(x) представляет собой полином степени n, при n=2 данное уравнение называется квадратным уравнением.
При решении такого рода уравнения необходимо выполнить те же действия, что и при решении линейных уравнений.
Квадратное уравнение.
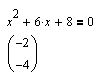
|
Команда Solve (Вычислить) подменю Variable (Переменные) меню Symbolics (Символы) дает решение в виде вектора: L={-2, -4}.
<
|
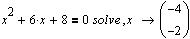
|
Аналогичный результат можно получить, используя директивы системы Smartmath.
|
Для этого необходимо включить панель символьных преобразований и после ввода выражения нажать кнопку со словом solve. В шаблоне, появившемся после вставки ключевого слова, необходимо указать переменную, относительно которой решается уравнение.
Другой способ решения заключается в использовании команды Factor (Фактор) меню Symbolics (Символы) для разложения полинома на множители в соответствии с теоремой Виета:
|
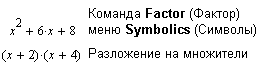
|
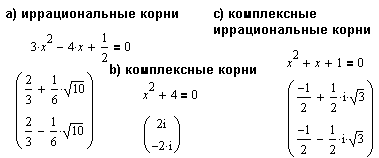
|
Отметим, что при иррациональных и комплексных решениях команда Factor (Фактор) меню Symbolics (Символы) не работает.Но MathCAD находит и такие решения при использовании команды Solve
|
Квадратные уравнения с комплексными коэффициентами.
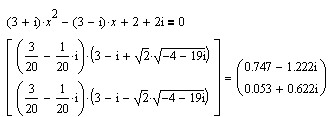
|
: При вводе уравнения с комплексными коэффициентами Сследует вводить для i: 1i; для -i: -1i; для 2i: 2i; ни в коем случае не вводить "*"! Как видим, MAthCAD неплохо справляется и с такими задачами.
|
Уравнения более высокого порядка.
Mathcad может решать уравнения вплоть до порядка 4 (даже символьно). Если возможно частичное разложение на множители, то разрешимы уравнения и более высокого порядка.
Кубические уравнения.
|
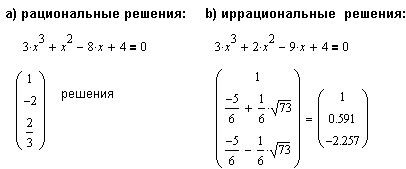
|

|
Уравнение седьмого порядка. 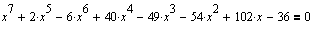 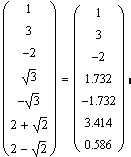
|

| Иррациональное уравнения (уравнения с радикалами). |
Корни (радикалы) могут вычисляться в MathCAD либо при помощи знака корня (клавиши [Ctrl+\]), либо как степени (клавиша [^] с дробными показателями. Знак квадратного корня вводится нажатием клавиши [\]. Знак корня и квадратный корень можно найти на панели Calculator (Калькулятор). Последовательность действий при решении уравнений с радикалами та же, что и при решении рассмотренных ранее уравнений.
С точки зрения теории, между решениями уравнений с радикалами и решением алгебраических уравнений имеется два важных различия, по крайней мере, при нахождении действительных решений.
Радикалы определены не везде в действительной области. Это обстоятельство приводит к необходимости находить область определени, прежде чем решать само уравнение. Данная проблема справедливо игнорируется MathCAD, поскольку он не может знать, во множестве каких чисел (действительных или комплексных) вы намерены решать уравнение. Выход: вы можете самостоятельно найти область определения, воспользовавшись при этом возможностями MathCAD, связанными с решениями неравенств.
Вторая проблема, возникающая при решении уравнений с радикалами, имеет принципиальный характер. Функция x2 (как и любая другая функция с четным показателем) на является инъективной (проблема главных значений). В связи с этим возведение в квадрат обеих частей уравнения, содержащего квадратные корни, не является эквивалентным преобразованием. Как всегда, при применении к обеим частям уравнения не инъективного преобразования увеличивается множество решений. В результате в него могут войти "фиктивные" решения. Как ни удивительно, MAthCAD сам производит проверку решений на "фиктивность".
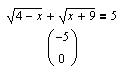
|
Классический случай решения уравнения с радикалами.
|
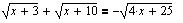 
|
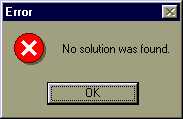
Mathcad распознает "фиктивные" решения (которые могут возникнуть в результате неэквивалентного преобразования "возведение в квадрат") и выдает верное сообщение: Решение не найдено. L = { }
|
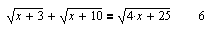 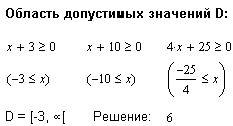
|
В приведенных примерах демонстрируется способность MathCAD находить область определения иррационального уравнения путем решения неравенств.
|
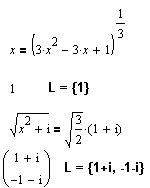
|
Уравнения с радикалами третьей степени, как и уравнения с комплексными коэффициентами, не представляют для MathCAD никакой сложности.
|
Уравнения с параметрами.
При решении уравнений с параметрами MathCAD ведет себя по-разному, в зависимости от того, каким образом производятся символьные вычисления - с помощью символьного знака равенства или команд меню Symbolics.
В данном примере использование палитры символьных преобразований позволяет решить уравнение (solve) и упрстить результат (simplify)
|
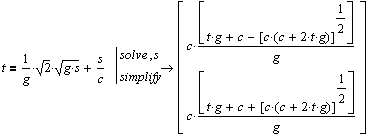
|
Экспоненциальные и логарифмические уравнения. |
Определение: Уравнение, в котором независимая переменная входит в аргумент хотя бы одной экспоненциальной (логарифмической) функции, называется экспоненциальным (логарифмическим) уравнением.
Способ решения с помощью Mathcad такой же, как и для других типов уравнений.
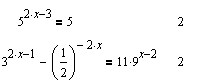
|
Экспоненциальные уравнения во множестве действительных чисел не создают дополнительных сложностей в том смысле, что их область определения совпадает со множеством действительных чисел, а логарифмирование представляет собой инъективное отображение.
|
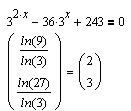
|
Если при решении экспоненциального уравнения возникают проблемы,их,как правило,можно устранить посредством вспомогательного логарифмирования. В крайнем случае можно обратиться к численным методам (См. Решение нелинейных уравнений и систем).
|
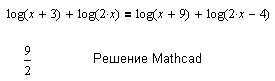
|
Значительно больше сложностей возникает при решении логарифмических уравнений. Область определения этих уравнений, если рассматривать их во множестве действительных чисел, как правило, не совпадает с действительной числовой прямой. MathCAD рассматривает логарифмические уравнения в комплексной области, т.е. не учитывая область определения.
|
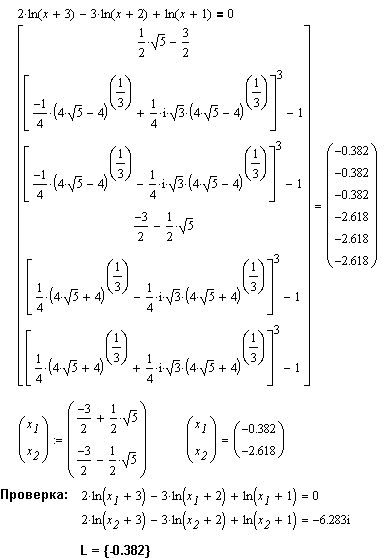 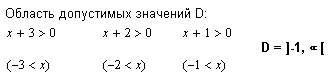
|
В данном примере показано, что MathCAD иногда находит решения (и даже действительные) там, где их быть не может (проблемы с комплексным логарифмом). Но нахождение области определения позволяет придти к верному решению.
|
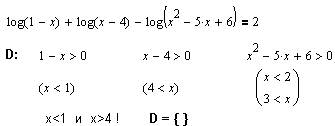
|
Насколько полезным может быть предварительное нахождение области определения, показывает следующий пример. Область определения пустое множество, следовательно,множество решений L={}.
|

| Тригонометрические уравнения. |
Сложность решения уравнений, содержащих тригонометрические функции, состоит прежде всего в том, что функций, обратных к тригонометрическим, не существует, а существуют лишь бесконечно многозначные обратные отображения. Поэтому прихдится мириться с тем, что любое вычислительное средство сможет найти только главное значение обратного выражения. Чтобы получить множество решений, необходимо самостоятельно воссоздать побочные значения обратного отображения.
Для тангенса (и котангенса) этого главного значения достаточно посредством периодического продолжения atan(x)+kp, где k - целое представить все решения. При решении уравнений с тангенсами и котангенсами возникает также вполне разрешимая проблема, связанная с тем, что данные функции определены не во всех точках числовой прямой.
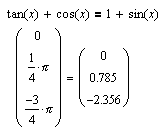
|
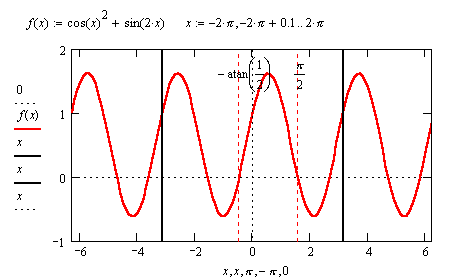
Данный пример показывает, что вышеуказанное ограничение не играет особой роли при решении уравнений с помощью MathCAD. Поскольку синус и косинус определены для всех значений аргумента, вопрос об области определения при решении уравнений, содержащих только эти тригонометрические функции, как правило, отпадает.
|
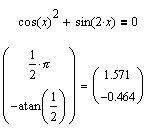
|
<
Вместо этого возникает другая сложность: обратные функции asin(x) и acos(x), значениями которых являютмя главные значения обратных отображений, не дают всех решений в рамках одного периода (2p).
|
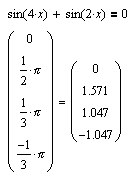
|
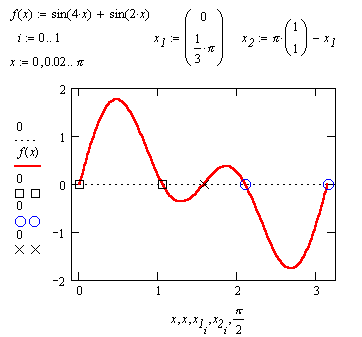
Поскольку остается неясным, какое именно из значений обратного отображения MathCAD рассматривает в качестве главного при решении уравнений, оказывается сложно получить еще одно значение, отстоящее от главного менее чем на период; тем самым задача была бы решена с точностью до периода. В подобных ситуациях на выручку приходит построение графиков.
|

|
Данный пример демонстрирует пределы возможности MathCAD. Решение в лоб не дает никаких результатов.
|
<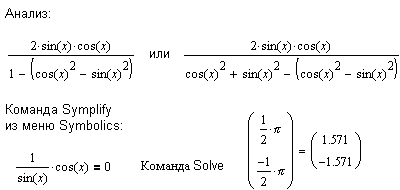
|
Проведя дополнительные преобразования, нам все-таки удается найти решение.
|

| Неравенства. |
MathCAD обладает достаточно мощными возможностями для решения неравенств. Эти возможности уже использовались нами ренее для нахождения области определения уравнений, содержащих функции, определенные не во всех точках числовой прямой.
Неравенства, как и уравнения, можно решать либо с использованием символьного знака равенства, либо, отметив переменную следм курсора, посредством выполнения команды Solve (Вычислить) подменю Variable (Переменные) меню Symbolics (Символы). В разных неравенствах могут быть использованы различные знаки неравенств.
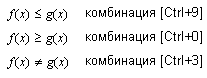
|
Знаки "больше" и "меньше" могут вводиться непосредственно с клавиатуры. Все остальные знаки можно вводить при помощи панели Evaluation (Вычисления), либо сочетанием клавиш.
|
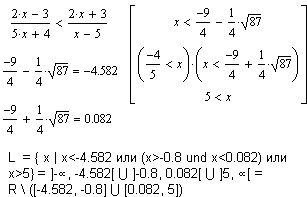
|
Линейные неравенства и неравенства с дробно-рациональными функциями не составляют сложности для MathCAD.
|
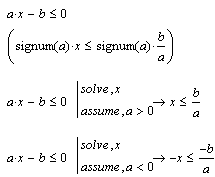
|
Неравенства с параметрами удобно анализировать с использованием знака символьного равенства, если значения параметра ограничены некоторыми условиями.
|
|
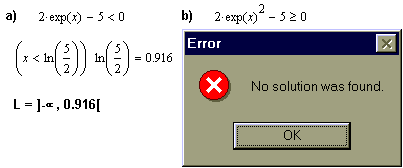
При решении неравенств, содержащих трансцендентные функции,возможности MathCAD ограничены.
|
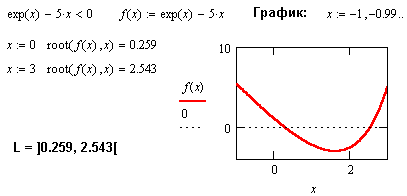
|
В данном примере MathCAD не может решить неравенство при использовании символьного процессора. На помощь приходят графики и функция численного решения уравнений root. Для работы этой функции необходимо задать начальное приближение для искомого решения.
|

| Системы линейных уравнений. |
Для численного решения линейных систем уравнений в MathCAD имеется специальная функция:
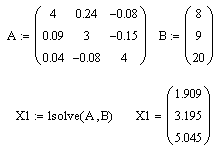
|
lsolv(A,B) Она решает систему линейных алгебраических уравнений вида А x X =B, выдавая решение - вектор X.
А - матрица коэффициентов размерности nxn;
В - вектор свободных членов размерности n ;
X - вектор неизвестных пока решений.
|
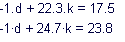
|
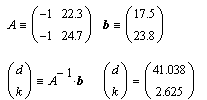
|
Эквивалентной для MathCAD формой представления систем линейных уравнений является матричная форма. Представленные таким образом системы можно решать как символьно, так и численно.
|
Хорошей альтернативой решению систем в матричной форме является так называемый solve block (Блок решения). Он удобен тем, что при его использовании уравнения записываются не в матричной, а в обычной форме, а также тем, что позволяет решать нелинейные уравнения и вводить ограничительные условия для определяемого решения. Блок решения применяется как для нахождения численного решения, так и для отыскания решеня в символьном виде.
Синтаксис Блока решения:
Given
Уравнения
Ограничительные условия
Find(v1,v2,...vn) - возвращает значение одной
или ряда переменных для точного решения
vi - переменные, которые надо найти.
Последовательность действий при численном решении:
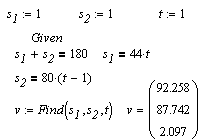
|
Задаем начальные (стартовые) значения для искомых переменных.
Заключаем уравнения в блок решения, начинающийся ключевым словом Given и заканчивающийся ключевым словом Find(v1,v2,...vn).
Если после слова Find(v1,v2,...vn) ввести знак равенства [=], MathACD выдаст численное решение.
|
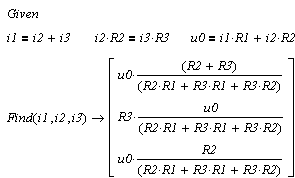
|
При символьном решении не надо вводить начальные значения, а после ключевого слова Find(v1,v2,...vn) вместо знака равенства следует ввести символьный знак равенства (при помощи комбинации [Ctrl+.] или соответствующей пиктограммы панели Evaluation).
|
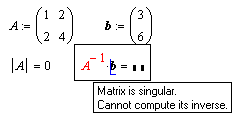 
|
Существует еще одно важное отличие между блоком решения и использованием матричных операций. Если определитель матрицы коэффициентов равен нулю, матричные методы оказываются непригодными. В таком случае система не имеет решений или разрешима неоднозначно. Если же применить блок решения, MathCAD распознает неоднозначность и выдает решение в параметрической форме.
|

| Нелинейные уравнения и системы уравнений. |
Многие уравнения, например трансцендентные, и системы из них не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью (не более значения, заданного системной переменной (TOL). Для простейших уравнений вида F(x)=0 решение находится с помощью функции
Rооt(Выражение, Имя_переменной)
Эта функция возвращает значение переменной с указанным уровнем точности, при котором выражение дает 0.
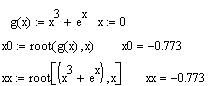
|
Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно, если возможно несколько решений. Тогда выбор решения определяется выбором начального значения переменной. Пример ниже иллюстрирует технику применения функции root для вычисления корней кубического полинома.
|
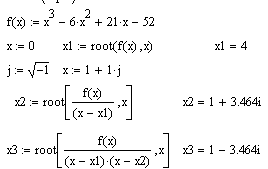
|
Как известно, кубическое уравнение обязательно имеет хотя бы один кубический корень х1. Он найден вначале функцией root. Два других корня могут оказаться и комплексными. Функция root может отыскивать и такие корни. Для поиска второго корня, х2, первый исключается делением F(x) на (х-х1). Соответственно для поиска третьего корня, хЗ, F(X) делится еще и на (х-х2).
|
Эту процедуру можно распространить и на поиск корней полиномов более высокой степени, однако надо помнить, что найти корни полинома можно гораздо более изящным и простым способом - используя операцию символьных вычислений.
Функция поиска корней многочлена polyroots
Для поиска корней обычного полинома р(х) степени п MathCAD содержит очень удобную функцию:
polyroots(V)
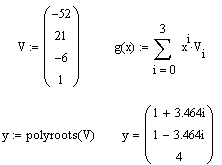
|
Она возвращает вектор корней многочлена (полинома) степени п, коэффициенты которого находятся в векторе V, имеющем длину равную п+1.
Заметим, что корни полинома могут быть как вещественными, так и комплексными числами. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой-шестой, так как тогда трудно получить малую погрешность вычисления корней.
|
При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый служебным словом — директивой Given — и имеющий следующую структуру:
Given
Уравнения
Ограничительные условия
Выражения с функциями Find и Minerr
В блоке используется одна из следующих двух функций:
Find(vl, v2, ..., vn) — возвращает значение одной или ряда переменных для точного решения;
Minerr(vl, v2, ..., vn) — возвращает значение одной или ряда переменных для приближенного решения.
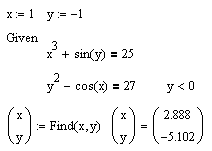
|
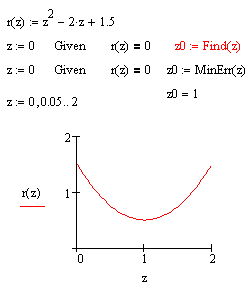
Между этими функциями существуют принципиальные различия. Первая функция используется, когда решение реально существует (хотя и не является аналитическим). Вторая функция пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения.
|
|
При использовании функции Minerr для решения систем нелинейных уравнений надо проявлять известную осторожность и обязательно предусматривать проверку решений. Нередки случаи, когда решения могут оказаться ошибочными, чаще всего из-за того, что из нескольких корней система предлагает нереальный (или не представляющий интереса) корень. Полезно как можно точнее указывать начальные приближения к решению.
|
5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Численное решение задачи Коши для дифференциальных уравнений и систем.
Решение граничных задач для обыкновенных дифференциальных уравнений.

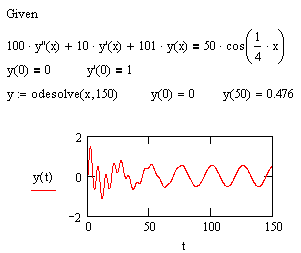
| Решение одиночного дифференциального уравнения. |
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) - Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x - переменная интегрирования, действительное число
b - конечная точка отрезка интегрирования
step - величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
Уравнение должно быть линейным относительно старшей производной.
Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ' (штрих) - [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
Конечная точка должна быть больше начальной.
Не допускаются начальные и граничные условия смешанного типа (f '(a)+f(a)=5).
Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))

| Численное решение задачи Коши для дифференциальных уравнений и систем. |
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F) - возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x
rkadapt(y,x1,x2,n,F) - ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed
Bulstoer(y,x1,x2,n,F) - дает более точное решение (методом Bulirsch-Stoer)
Агрумкнты вышеуказанных функций:
y - вектор начальных условий
x1,x2 - границы интервала для поиска решения
n - количество точек на интервале
F(x,y) - вектор-функция первых производных
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
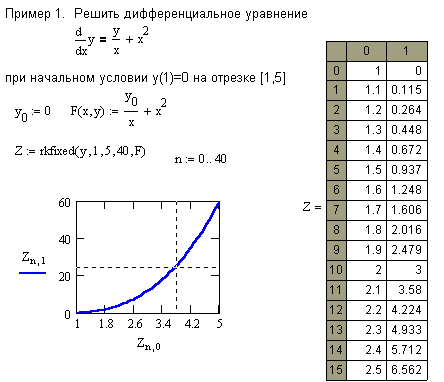 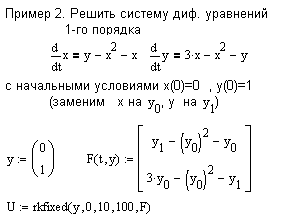
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй - значение функции, третий - для диф. уравнений 2-го порядка - значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M< >
 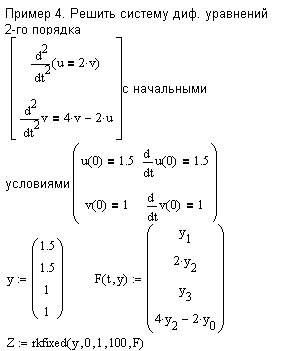
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr
Stiffb(y,x1,x2,n,F,J) - ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer
Stiffr(y,x1,x2,n,F,J) - ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock
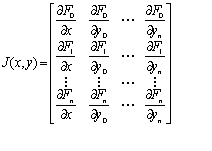
|
Первые пять аргументов такие же,как и при решении хорошо обусловленных систем дифференциальных уравнений . Дополнительный аргумент - матрица J размером nx(n+1), первый столбец которой содержит частные производные dF/dx, остальные столбцы и строки представляют собой матрицу Якоби dF/dy
|
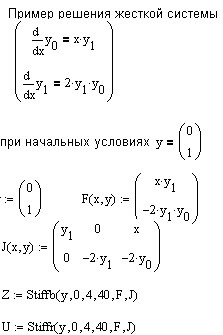
|
Пример решения жесткой системы дифференциальных уравнений.
|
Для отыскания решения системы диф. уравнений только в конечной точке используются функции bulstoer,rkadapt, stiffb, stiffr (начинаются с прописной буквы).

|
Набор парамтров для этих функций :
bulstoer(y,x1,x2,acc,F,kmax,save)
rkadapt(y,x1,x2,acc,F,kmax,save)
stiffb(y,x1,x2,acc,F,J,kmax,save)
stiffr(y,x1,x2,acc,F,J,kmax,save)
|
Первые три параметра и пятый (F) этих функций те же, что идля функции Rkadapt. Дополнительные параметры:
acc - параметр, контролирующий точность решения (реком. асс=0.001)
kmax - максимальное число промежуточных точек в которых ищется решение
save - минимально допустимый интервал между точками, в которых ищется решение

| Решение граничных задач для обыкновенных дифференциальных уравнений. |
Если для дифференциального уравнения n-го порядка k граничных условий заданы в начальной точке х1, а (n-k) граничных условий - в конечной точке х2, то такая задача называется краевой. В MathCAD реализованы две функции, позволяющие численно найти недостающие условия в точках х1 и х2.
Двухточечная краевая задача
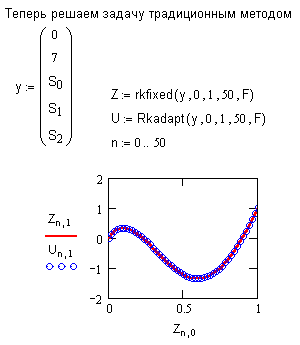
Задача решается в два этапа. Сначала с помощью функции sbval находятся недостающие начальные значения, а затем применяется одна из выше описанных функций для решения стандартной задачи Коши на отрезке.
sbval(v,x1,x2,F,load,score) - ищет недостающие начальные условия в точке х1
v - вектор началных приближений для искомых начальных значений в точке х1,
х1,х2 - граничные точки интервала
F(x,y) - вектор-столбец из n элементов, содержит правые части дифференциальных уравнений
load(x1,v) - вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(x2,y) - вектор-столбец размерности вектора v, содержащий разность между начальным условием в точке х2 и значеием искомого решения в этой точке.
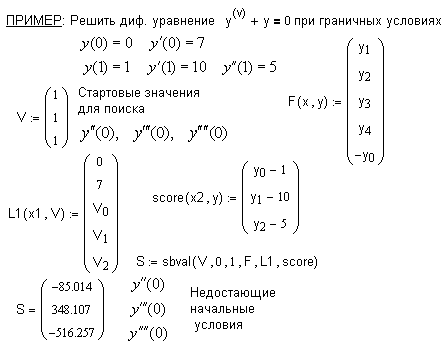 
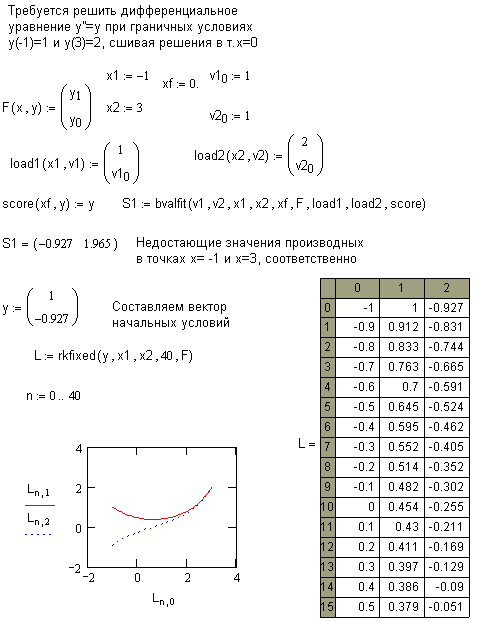
Краевая задача с условиями внутри интервала.
На первом этапе используется функция
balfit(V1,V2,x1,x2,xf,F,load1,load2,score) - ищет недостающие начальные условия в точках х1 и х2, сшивая решения, выходящие из этих точек, в точке xf
V1,V2 - вектора началных приближений для искомых начальных значений в точках х1 и х2
х1,х2 - граничные точки интервала
load1(x1,V1) - вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения
load2(x2,V2) - вектор-столбец из n элементов, содержит начальные значения в точке х2; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(xf,y) - вектор-столбец размерности n, содержащий разность между решениями, начинающимися в точках х1 и х2, в точке xf
Программирование в MathCAD.
6.1 Обзор программных операторов.
6.2 Примеры программ.
6.3 Задание.

|
 Скачать 1.69 Mb.
Скачать 1.69 Mb.