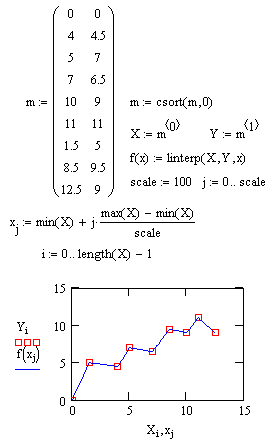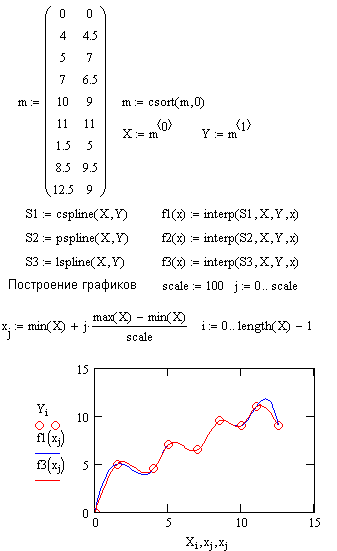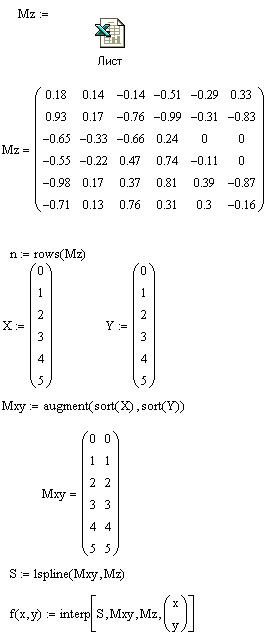|
|
Лабы и лекции по Mathcad. 1. 1 Интерфейс пользователя
7.1 Функции линейной и сплайновой аппроксимации.
   
Одномерная линейная аппроксимация.
Одномерная сплайн-интерполяция и сплайн-аппроксимация.
Двумерная линейная сплайн-интерполяция и сплайн-аппроксимация.

| Одномерная линейная аппроксимация. |
При проведении научно-технических расчетов часто используются зависимости вида у (х), причем число точек этих зависимостей ограничено. Неизбежно возникает задача получения приемлемой представительности функций в промежутках между узловыми точками (интерполяция) и за их пределами (экстраполяция). Эта задача решается аппроксимацией исходной зависимости, т. е. ее подменой какой-либо достаточно простой функцией. Система MathCAD предоставляет возможность аппроксимации двух типов: кусочно-линейной и сплайновой.
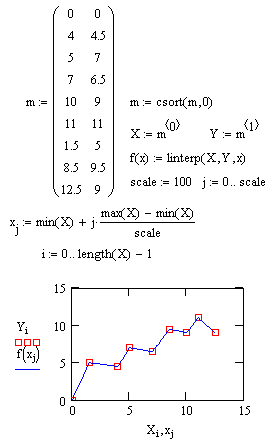
|
При кусочно-линейной интерполяции, или аппроксимации, вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает просто соединение узловых точек отрезками прямых, для чего используется следующая функция:
linterp(VX, VY, х)
Для заданных векторов VX и VY узловых точек и заданного аргумента х эта функция возвращает значение функции при ее линейной аппроксимации. При экстраполяции используются отрезки прямых с наклоном, соответствующим наклону крайних отрезков при линейной интерполяции.
|

| Одномерная сплайн-интерполяция и сплайн-аппроксимация. |
При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. Для целей экстраполяции функция linterp не предназначена и за пределами области определения может вести себя непредсказуемо.
Гораздо лучшие результаты дает сплайн-аппроксимация. При ней исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные.
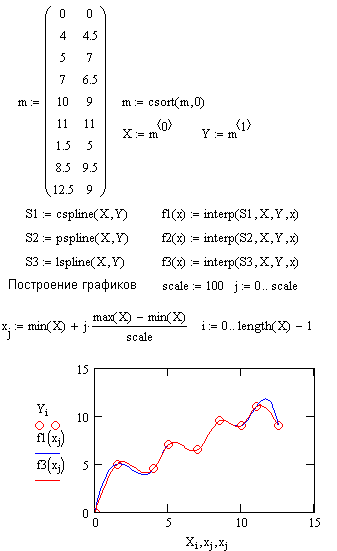
|
Для осуществления сплайновой аппроксимации система MathCAD предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн-функций при различном виде интерполяции:
cspline(VX, VY) — возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;
pspline(VX, VY) — возвращает вектор VS вторых производных при приближении к опорным точкам параболической кривой;
lspline(VX, VY) — возвращает вектор VS вторых производных при приближении к опорным точкам прямой.
Наконец, четвертая функция
interp(VS, VX, VY, x)-возвращает значение у (х) для заданных векторов VS, VX, VY и заданного значения x.
|
Таким образом, сплайн-аппроксимация проводится в два этапа. На первом с помощью функций cspline, pspline или Ispline отыскивается вектор вторых производных функции у (х), заданной векторами VX и VY ее значений (абсцисс и ординат). Затем, на втором этапе для каждой искомой точки вычисляется значение у (х) спомощью функции interp.

| Двумерная линейная сплайн-интерполяция и сплайн-аппроксимация. |
Для повышения качества построения ЗD-графиков имеется возможность осуществления двумерной сплайн-интерполяции. Это позволяет существенно повысить представительность сложных графиков SD-функций, в том числе контурных.
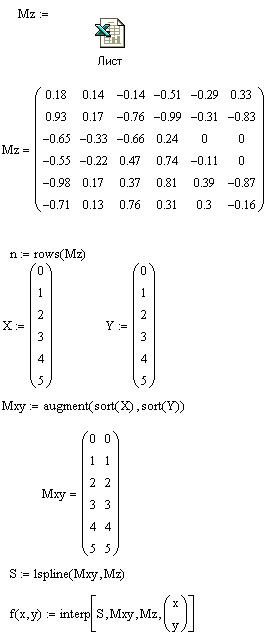
|
|
Интерполяция функции 2-х переменных проводится также в два этапа:
1. Вычисляется вектор VS вторых производных в опорных точках с помощью функций
cspline(Mxy,Mz),
pspline(Mxy,Mz),
lspline(Mxy,Mz)
.
Здесь Mxy - матрица размера n*2, сторки которой определяют по диагонали (x,y)координаты прямоугольной сетки,
Mz - матрица размера n*n значений функции в узлах вышеопределенной сетки.
2. Вычисление с помощью функции interp(VS,Mxy,Mz,V). Здесь V - вектор координат (x,y).
|
|
|
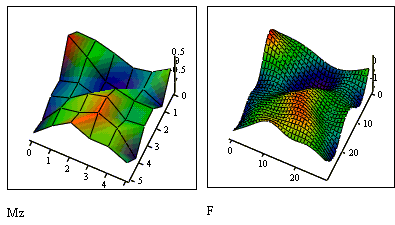
На рисунке справа показан график функции 2-х переменных после проведения двумерной сплайн-интерполяции, а слева - без нее.
|
|
|
 Скачать 1.69 Mb.
Скачать 1.69 Mb.