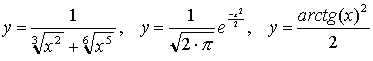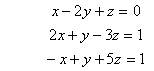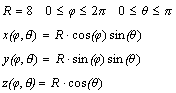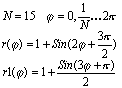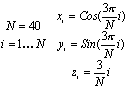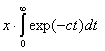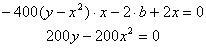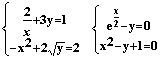|
|
Лабы и лекции по Mathcad. 1. 1 Интерфейс пользователя
7.3 Функции сглаживания данных.
   
Данные большинства экспериментов имеют случайные составляющие погрешности. Поэтому часто возникает необходимость статистического сглаживания данных. Ряд функций MathCAD предназначен для выполнения операций сглаживания данных различными методами. Вот перечень этих функций:
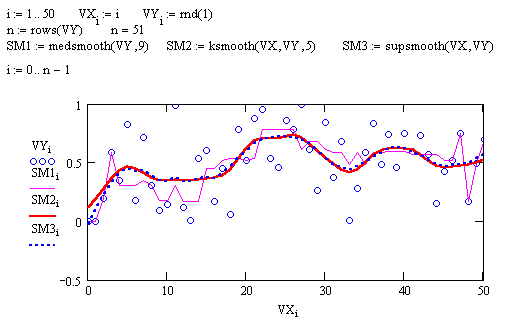
medsmooth(VY,n)— для вектора с m действительными числами возвращает m-мерный вектор сглаженных данных по методу скользящей медианы, параметр n задает ширину окна сглаживания (n должно быть нечетным числом, меньшим m);
ksmooth(VX, VY, b) — возвращает n-мерный вектор сглаженных VY, вычисленных на основе распределения Гаусса. VX и VY — n-мерные векторы действительных чисел. Параметр b (полоса пропускания) задает ширину окна сглаживания ( b должно в несколько раз превышать интервал между точками по оси х );
supsmooth(VX, VY) — возвращает n-мерный вектор сглаженных VY, вычисленных на основе использования процедуры линейного сглаживания методом наименьших квадратов по правилу k-ближайших соседей с адаптивным выбором k. VX и VY — n-мерные векторы действительных чисел. Элементы вектора VX должны идти в порядке возрастания.

7.4 Функция предсказания.
   
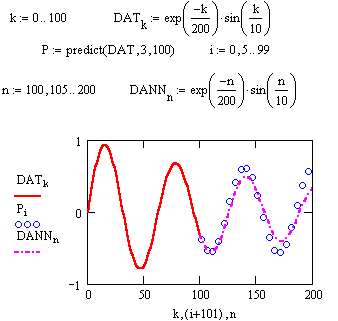
Весьма интересной является функция предсказания predikt(data,k,N), где data — вектор данных,
|
где data — вектор данных, k — число последних точек существующих данных, на основе которых происходит расчет предсказываемых точек; и N — число точек, в которых необходимо предсказать данные. Она по ряду заданных равномерно расположенных точек позволяет рассчитать некоторое число N последующих точек, т. е. по существу выполняет экстраполяцию произвольной (но достаточно гладкой и предсказуемой) зависимости.
|
Функция предсказания обеспечивает высокую точность при монотонных исходных функциях или функциях, представляемых полиномом невысокой степени.
Лабораторная работа №1.
   
Вычислите для каждого значения Х=1,5,7 следующие функции:
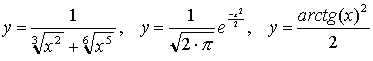
Рекомендуется использовать операцию векторизации (MathPalette, матричные операции) Измените количество значащих цифр , выводимых на экран после десятичной точки, на 6.
Решите двумя способами (матричным и с помощью функции lsolve ) систему линейных уравнений,
Справку по использованию функции lsolve найдите в справочной системе MathCAD.
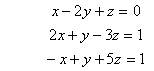
Смените нижнюю границу индексации массивов на 1.Выведете решение системы уравнений из п.2 в виде вектора-столбца и поэлементно.
Скопируйте первую из формул п.1 и замените в ней первое подкоренное выражение в знаменателе на sin(x) , а второй операнд в знаменателе - на ctg(x/2). Присвойте полученное выражение новой переменной G ( удалив у) .
Вставьте в документ текстовую область: "Построение простейшего графика."
Определите функцию f(x)= sin(x)+cos(x)-1.
Постройте график функции f(x)(воспользуйтесь быстрым построением графиков).
Лабораторная работа №2.
   
Задайте вектор V1, состоящий из трех элементов {2,3,1}, и вектор V2 - {4,1,7}.
Выполните следущие операции: V1*3, V1-V2, V1*V2, V1xV2, прсуммируйте элементы V1, транспонируйте вектор V2, вычислите норму вектора V1; используя операцию векторизации, вычислите Sin(V1) и посчитайте норму получившегося вектора.
Задайте матирицу М с размерностью 2x3, транспонируйте ее.
Создайте единичную матрицу Е размерности 5x5, вычислите ее след.
Создайте две квадратные матрицы М1 и М2 размерности 3x3,перемножьте их; у полученной матрицы вычислите определитель, выведите на экран второй столбец, и поэлементно третью строку.
Сложите матрицы М1 и М2 (матрица ММ), для полученной матрицы вычислите ехр(ММ).
Объедините матрицу ММ и вектор V1, отсортируйте полученную матрицу по первым столбцу и строке.
Вычислите собственные значения любой из введенных матриц размерности 3x3, а также собственный вектор, принадлежащий второму собственному значению.
Лабораторная работа №3.
   
Построение графиков функций, заданных явным выражением.
Задайте ранжированную переменную х, меняющуюся от 0 доp/2 с шагом 0.1; определите функцию f(x) = x*Sin(2x)2 , постройте ее график.
Определите изменение целого индекса i от нуля до 15,
xi = i/10, yi = xiSin(2xi)2, постройте график функции yi(xi).
Постройте график функции g(x,y) =x2 - y2, где переменные x и y меняются от -5 до 5.
Построение графиков функций, заданных параметрически.
Изобразите сферу. Ее параметрическое представление имеет вид:
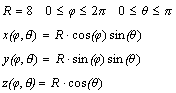
Число точек N=30.
Анимация. Измените определение радиуса сферы R(f)=|cos(FRAMEf)|. Постройте анимационный график (число кадров равно 20, число кадров в секунду - 3. Просмотрите на Плеере получившуюся анимацию.
ВНИМАНИЕ!!! Перед построением анимации не забудьте отключить АВТОМАСШТАБ!!!
Постройте графики функций, заданных полярно:
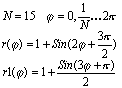
Изобразите пространственную кривую:
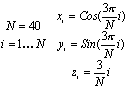
Увеличьте число точек N, повторите построение предыдущего графика; поэкспериментируйте, меняя различные параметры отображения графика .
Лабораторная работа №4.
   
Используя команды меню Symbolic, вычислите в символьном виде:
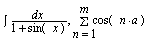
Разложите по степеням Sin(5x); Посчитайте производную от полученного выражения. Постройте график функции и ее представлений в виде ряда, включающих 2 члена разложения, 5 членов разложения и 10 членов разложения.
Вычислите коэффициенты полинома по степеням х и у:
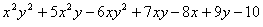
Используя интегральное преобразование Лапласа ( и обратное преоразование Лапласа) решите в символьном виде дифференциальное уравнение
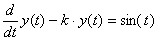
Используя палитру символьных преобразований, найдите точку, в которой функция двух переменных имеет экстремум
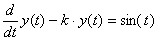
Вычислите в символьном виде интеграл, предположив, что с - действительное число, с>0:
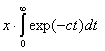
Используя оператор символьного вывода и блок Given… Find, Решите в символьном виде систему уравнений:
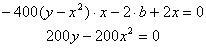
Вычислите предел от функции tg(x) при х стремящемся к p/2- обыкновенный, слева и справа.
Исследуйте аналитически функцию f(x): определите точки максимума и минимума, точки перегиба, постройте графики f(x), f ' (x) и f "(x)
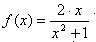
Лабораторная работа №5.
   
Найдите решения систем уравнений (если они существуют !) с помощью блоков Given…Find, Given…Minner. Проверьте, все ли решения найдены.
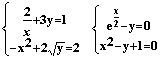
Решите на отрезке [0,3] задачу Коши используя:
а) функцию odersolve (в блоке с Given)
b) функцию rkfixed. Выведите значение полученного решения в точке x=3.
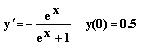
Решите задачу Коши для дифференциального уравнения на отрезке [0,1], используя:
а) функцию odersolve (в блоке с Given)
b) функцию rkadapt..
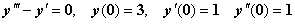
Решите систему дифференциальных уравнений на отрезке [0,3]. Выведите значения искомых функций и их производных в точке с координатой х=1.5
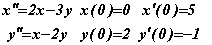
Решите краевую задачу для дифференциального уравнения на отрезке [0,8], выведите значение функции и ее производных в конечной точке отрезка.
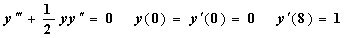
Для примера из п.4 вычислите значение функции только в конечной точке. (используйте специально предназначенные для этого формы функций bulstoer, rkadapt, stiffb, stiffr )
Найдите корни многочлена y(x) = 2x3 + 20 x2 - 2x + 100 с помощью функций root и poltroots. (Обратите внимание на значение системной переменной TOL).
Лабораторная работа №6.
   
Составьте программу, вычисляющую константу, фигурирующую в легенде об изобретателе шахмат. Изобретатель попросил дать ему в награду определенное количество зерна, положив на первую клетку одно зернышко ( 2 1-1 , т.е. 2 0), на вторую - два зернышка (2 2-1), на третью - четыре (2 3-1) и т.д. (на новой клетке зерен в 2 раза больше, чем на предыдущей). Найдите общее число зерен, составляющих награду изобретателя. Вычислите их массу, приняв за массу одного зерна 0,3 грамма. Переведите полученный результат в тонны. Вы знаете это число ??? А MathCAD знает!!!
Модифицируйте программу, предусмотрев выход из неё, если число зерен больше триллиона (10 12).
Составьте программу-функцию, вычисляющую по заданным длинам сторон треугольника а, в, с три величины: периметр треугольника, его площадь и радиус вписанной окружности ( s=[p(p-a)(p-b)(p-c)]1/2 , r = [(p-a)(p-b)(p-c)/p]1/2 , где p - полупериметр). Предусмотрите в программе оценку существования треугольника с заданными длинами сторон а, в, с и выдачу результата об ошибке, если треугольник с указанными сторонами не существует.
Составьте программу-функцию, вычисляющую n коэффициентов разложения функции f(x), заданной на отрезке[-L,L], в ряд Фурье - т.е. параметрами являются f, n, L.
Используя построенную в п.4 функцию, вычислите приближение рядом Фурье ступенчатой функции, заданной на [-1,1]:
f(x) = 0, если -1
   
Лабораторная работа № 7.
1. Введите матрицу координат точек плоскости:
-
х
|
0.1
|
5
|
1.1
|
0.5
|
3.4
|
2.7
|
1.9
|
4
|
4.7
|
у
|
10
|
1.3
|
5
|
7
|
3
|
4.5
|
6
|
2.5
|
1.5
|
А) Постройте линейную и сплайновую интерполяцию для данного облака точек.
Б) Постройте функции линейной,полиномиальной и обобщенной регрессии для этих же точек.
2. С помощью функции rnd введите 50 случайных чисел из отрезка [0,2]. Постройте функции сглаживания данных (с помощью различных встроенных функций).
3. Спомощью функции predict предскажите поведение функции f(x)=Sin(2*x) на [2p,4p], если предположить, что она задана на отрезке [ 0,2p] . Изменится ил предсказанное поведение, если в качестве исходных данных взять функцию, определенную на [0,p] ?
|
|
|
 Скачать 1.69 Mb.
Скачать 1.69 Mb.