Прикладная механика. Шпоры. 13 Геометрический метод сложения сил
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Физическая сторона задачи о плоском изгибе. Используя закон Гука при осевом растяжении, получаем 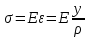 . .Подставив в выражение, отражающее статическую сторону задачи о плоском изгибе, значение 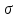 , получаем , получаем 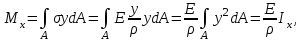 откуда 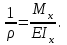 Подставив значение 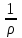 в исходную формулу, получаем в исходную формулу, получаем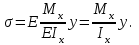 Данное выражение отражает физическую сторону задачи о плоском изгибе, которое дает возможность рассчитать нормальные напряжения по высоте сечения. Хотя это выражение получено для случая чистого изгиба, но как показывают теоретические и экспериментальные исследования, оно может быть использовано и для плоского поперечного изгиба. Нейтральная линия. Положение нейтральной линии определим из условия равенства нулю нормальной силы в сечениях балки при чистом изгибе 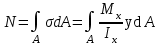 . .Так как 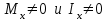 , то необходимо, чтобы нулю был равен интеграл , то необходимо, чтобы нулю был равен интеграл 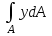 . Данный интеграл представляет собой статический момент сечения относительно нейтральной оси. Так как статический момент сечения равен нулю только относительно центральной оси, следовательно, нейтральная линия при плоском изгибе совпадает с главной центральной осью инерции сечения. . Данный интеграл представляет собой статический момент сечения относительно нейтральной оси. Так как статический момент сечения равен нулю только относительно центральной оси, следовательно, нейтральная линия при плоском изгибе совпадает с главной центральной осью инерции сечения.Касательные напряжения. Касательные напряжения, которые возникают в сечениях балки при плоском поперечном изгибе, определяются по зависимости: 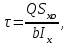 где 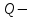 поперечная сила в рассматриваемом сечении балки; поперечная сила в рассматриваемом сечении балки;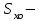 статический момент площади отсеченной части сечения относительно нейтральной оси балки; статический момент площади отсеченной части сечения относительно нейтральной оси балки;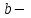 ширина сечения в рассматриваемом слое; ширина сечения в рассматриваемом слое;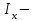 момент инерции сечения относительно нейтральной оси. момент инерции сечения относительно нейтральной оси.Касательные напряжения равны нулю в крайних волокнах сечения и максимальны в волокнах нейтрального слоя. 28 Расчет балок на прочность при изгибе. Прочность балки будет обеспечена, если будут выполняться условия: 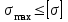 ; ; 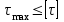 . .Максимальные нормальные напряжения при изгибе возникают в сечениях, где действует максимальный изгибающий момент, в точках сечения наиболее удаленных от нейтральной оси 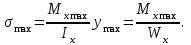 Максимальные касательные напряжения возникают в сечениях балки, где действует максимальная поперечная сила 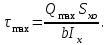 Касательные напряжения 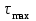 обычно малы по сравнению с обычно малы по сравнению с 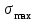 и в расчетах, как правило, не учитываются. Проверка по касательным напряжениям производится только для коротких балок. и в расчетах, как правило, не учитываются. Проверка по касательным напряжениям производится только для коротких балок.29 Гипотеза наибольших касательных. Эта гипотеза была выдвинута Кулоном в 1773 году и носит название третьей теории прочности. Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее касательное напряжение достигает значения, предельного для данного материала. При объемном напряженном состоянии 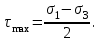 Условие прочности по третьей теории прочности имеет вид 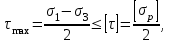 или или 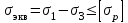 . .Во многих практических случаях третья теория прочности дает удовлетворительные результаты. Подставляя значения главных нормальных напряжений, выраженных через нормальные и касательные напряжения, получаем 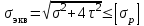 . .31 Понятие о сложном сопротивлении. К сложному сопротивлению относятся такие виды нагружения бруса, при которых в поперечных сечениях возникают одновременно не менее двух внутренних силовых факторов. Исключением является поперечный изгиб, который не принято рассматривать как случай сложного сопротивления, хотя в сечениях возникает изгибающий момент и поперечная сила. Это связано с тем, что в большинстве случаях расчеты на прочность и жесткость проводятся без учета влияние поперечной силы. Случаи сложного сопротивления можно словно разделить на две группы. К первой группе относятся такие случаи сложного сопротивления, когда в опасных точках бруса напряженное состояние является одноосным. В эту группу относят косой изгиб (рис. 27,а), изгиб с растяжением (рис. 27,б), внецентренное растяжение-сжатие (рис. 27,в) и др. При косом изгибе условие прочности имеет вид: 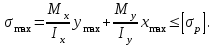 Условие прочности при изгибе с растяжением, пренебрегая действием поперечных сил, имеет вид:  Рис. 27 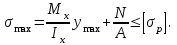 . .Ко второй группе относятся такие случаи сложного сопротивления, когда напряженное состояние является плоским. Например, изгиб с кручением (рис. 28). Для случая нагружения, относящейся к первой группе, в отличие от второй группы, нет необходимости в применении гипотез прочности. 32 Изгиб с кручением. На практике часто встречаются стержни круглого и некруглого сечения, подверженные одновременному действию крутящих и изгибающих моментов. Такому нагружению подвержены валы машин и механизмов и многих других конструкций. Для расчета бруса необходимо в первую очередь установить опасные сечения. Для этого необходимо построить эпюры изгибающих и крутящих моментов (рис. 28).  Рис. 28 Начнем с того, что, пользуясь принципом независимости действия сил, определим отдельно напряжения, возникающие в брусе при кручении, и отдельно при изгибе. От кручения в поперечных сечениях бруса возникают касательные напряжения, достигающие наибольшего значения в точках контура сечения 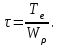 При изгибе в поперечных сечениях бруса возникают нормальные напряжения, достигающие наибольшего значения в крайних волокнах бруса 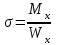 и касательные напряжения, достигающие наибольшего значения у нейтральной оси, и определяемые по формуле Журавского 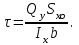 Эти напряжения значительно меньше напряжений от крутящего момента, поэтому ими пренебрегают. Опасное сечение бруса будет у заделки, где действуют максимальные напряжения от изгиба и кручения. Опасными точками будут точки 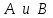 . .Рассмотрим напряженное состояние в наиболее опасной точке 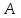 (рис. 29). Так как напряженное состояние двухосное, то для проверки прочности применяет одну из гипотез. (рис. 29). Так как напряженное состояние двухосное, то для проверки прочности применяет одну из гипотез. Рис. 29 Применим третью теорию прочности 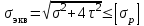 . .Учитывая, что 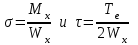 , получаем , получаем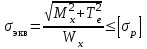 . .Отсюда для подбора сечения находим требуемый момент сопротивления 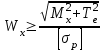 . .При проверочных расчетах, когда диаметр вала известен, коэффициент запаса прочности 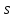 вычисляется по формуле вычисляется по формуле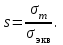 |
