Прикладная механика. Шпоры. 13 Геометрический метод сложения сил
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
19 Растяжением или сжатием называется такой вид нагружения, при котором в поперечных сечениях бруса возникает только продольная сила N, дейст-вующая перпендикулярно плоскости поперечного сечения. Многие детали и узлы авиатехники в процессе эксплуатации испытывают деформацию растяжения или сжатия. Болты и шпильки при затяжке растягива-ются. Тяги управления самолетом и двигателем, в зависимости от характера и режима полета, растягиваются или сжимаются. Растяжение и сжатие воспри-нимают полки лонжеронов, шатуны кривошипных механизмов, рама крепления двигателя к самолету, стойки шасси и т.д. Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют силы 2F и 3F (рис. 2.4). 1. Разбиваем брус на участки, границами которого являются точки приложения сосредоточенных сил или изменение поперечного сечения. 2. Методом сечений на каждом участке определяем продольные силы N1 и N2, начиная со свободного конца. Во всех точ-ках поперечного сечения бруса будут дей-ствовать внутренние распределенные си-лы, равнодействующая которых опреде-лится из условия равновесия одной из частей бруса. 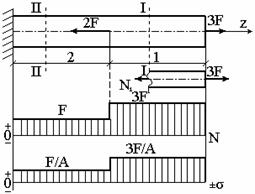 Рис. 2.4 Аналогично находим продольную силу N2: В пределах одного участка продольная сила будет иметь постоянное значение. Растягивающие продольные силы будем считать положительными, а сжимающие - отрицательными. 20. В расчетах прочности стержней при растяжении и сжатии необходимо знать механические свойства материалов. Эти свойства выявляются при испытаниях образцов на растяжение под нагрузкой.  График зависимости между растягивающей силой Fи удлинением образца ΔL называют диаграммой растяжения. График зависимости между растягивающей силой Fи удлинением образца ΔL называют диаграммой растяжения.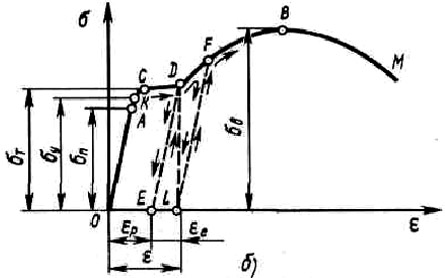 Диаграмму можно условно разделить на четыре зоны. Первая зона называется зоной упругости, здесь свойства материала на участке ОА подчиняются закону Гука. Вблизи точки Аможно отметить точку К, в которой после снятия нагрузки (разгрузки) в образце возникает остаточная деформация. Напряжение в точке К называют пределом упругости. Практически величина предела упругости близка к пределу пропорциональности материалов. Вторая зона KDназывается зоной общей пластичности. Для нее характерно существенное увеличение деформации (длины) образца без заметного увеличения напряжения (нагрузки). В этой зоне для некоторых материалов (например, малоуглеродистой стали) наблюдается почти горизонтальный участок — площадка текучести (отрезок CDдиаграммы). Третья зона DB– зона упрочнения; здесь удлинение образца более интенсивное по сравнению с зоной ОК. Если разгрузить образец в любой точке Fэтой зоны, то при последующем нагружении материал приобретает способность воспринимать без остаточных деформаций большие нагрузки. Явление повышения упругих свойств материала в результате предварительного пластического деформирования носит название наклепа или нагартовки и широко используется в технике. Так, например, цепи и тросы грузоподъемных машин, а иногда болты и пружины подвергают предварительному растяжению силами, превышающими рабочие, для того чтобы избежать остаточных удлинений в дальнейшем. Проволока, полученная волочением, выдерживает большие нагрузки, чем материал, из которого она изготовлена. Наклеп может быть снят термической обработкой — отжигом. Для этого материал нагревают до известной температуры, выдерживают при этой температуре в течение определенного времени, а затем медленно охлаждают. Четвертую зону ВМ называют з о ной местной текучести. Здесь удлинение образца происходит с уменьшением силы и сопровождается образованием местного сужения — шейки. При этом среднее напряжение в поперечном сечении шейки возрастает. В точке М наступает разрушение образца. У многих материалов разрушение происходит без заметного образования шейки. 2 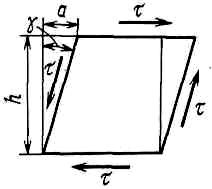 1 Сдвиг, внутренние силовые факторы и деформация. (Без внутренние силовые факторы, деформация гавно какое то). 1 Сдвиг, внутренние силовые факторы и деформация. (Без внутренние силовые факторы, деформация гавно какое то).Сдвиг- вид деформации, когда в поперечных сечениях стержня действует только перерезывающая сила, а остальные силовые факторы отсутствуют. Сдвиг соответствует действию на стержень двух равных противоположно направленных и бесконечно близко расположенных поперечных сил,вызывающих срез по плоскости, расположенной между силами (как при разрезании ножницами прутков, листов и т. п.). Срезу предшествует деформация — искажение прямого угла между двумя взаимно перпендикулярными линиями. При этом на гранях выделенного элемента возникают касательные напряжения τ. Напряженное состояние, при котором на гранях выделенного элемента возникают только касательные напряжения называется чистым сдвигом. Величина а называется абсолютным сдвигом, угол на который изменяются прямые углы элемента, называют относительным сдвигом, tgγ≈γ=a/h. Деформация. Если на боковую поверхность круглого стержня нанести сетку, то после закручивания можно обнаружить: образующие цилиндра обращаются в винтовые линии большого шага; сечения круглые и плоские до деформации сохраняют свою форму, и после деформации; происходит поворот одного сечения относительно другого на некоторый угол, называемый углом закручивания; расстояния между поперечными сечениями практически не изменяются. На основании этих наблюдений принимают гипотезы, что: сечения, плоские до закручивания, остаются плоскими после закручивания; радиусы поперечных сечений при деформации остаются прямыми. В соответствии с этим кручение стержня можно представить как результат сдвигов, вызванных взаимным поворотом сечений. Закон Гука при сдвиге. Р 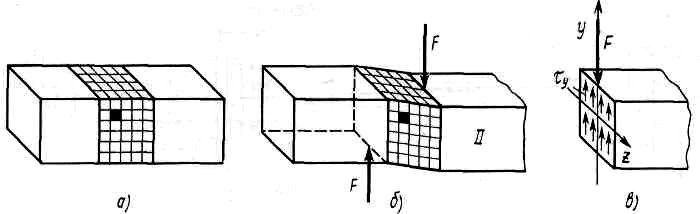 ассмотрим равновесие отсеченной правой части стержня . Действие отброшенной левой части на правую заменим внутренними силами упругости. Запишем уравнение равновесия(ΣY=0), найдем, что в сечении действует лишь перерезывающая сила Qy=F. Эта сила является равнодействующей касательных напряжений: Qy=∫AτydA. Касательные напряжения равномерно распределены по поперечному сечению площадью А, тогда τy=Qy/A=F/A. В пределах упругих деформаций величина сдвига, а пропорциональна сдвигающей силе F,расстоянию h,на котором происходит сдвиг, и обратно пропорциональна площади сечения А. Введем коэффициент пропорциональности G, зависящий от свойств материала, тогда закон упругости для сдвига выразится формулой: а=Fh/GA, где GA — жесткость сечения при сдвиге.Учитывая последние равенства, найдем выражение для закона Гука при сдвиге. τ=Gγ. Величина G называется модулем упругости при сдвиге (модулем сдвига). Между модулями упругости Е и сдвига G существует взаимосвязь: G=E/(2(1+μ)), μ - коэффициент Пуассона. 22. Построение эпюр крутящих моментов. Крутящий момент в сечении бруса определяется методом сечений. По модулю он численно сечения равен алгебраической сумме внешних моментов слева или справа от сечения. Брус разбивается на участке и на каждом участке проводится сечение (рис. 21).  Рис. 21 В каждом сечении определяется крутящий момент, а затем строится эпюра крутящих моментов. Для случая, изображенного на рис. 20, крутящие моменты в сечениях 1 и 2 будут равны 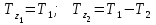 . .23 Расчеты на прочность и жесткость при кручении. Условие прочности при кручении имеет вид 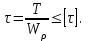 Условие жесткости при кручении 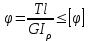 . .Для бруса круглого сечения эти условия имеют вид 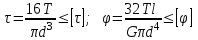 . .24 Кручением называют такой вид нагружения, когда в поперечных сечениях бруса возникает только один силовой фактор – крутящий момент. Брус, работающей на кручение называется валом. При кручении вала его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса.  Рис. 19 Рис. 19Напряжения и деформации при кручении бруса. Под действием внешнего скручивающего момента, приложенного на правом конце бруса, левый конец которого жестко закреплен, брус будет закручиваться. Выделим из бруса элементарный цилиндр длиной 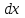 (рис. 19). Будем считать, что левое сечение бруса жестко закреплено. Под действием крутящего момента (рис. 19). Будем считать, что левое сечение бруса жестко закреплено. Под действием крутящего момента 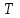 правое сечение повернется на некоторый угол правое сечение повернется на некоторый угол 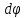 . .Из рис. 19 видно, что 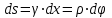 , откуда получаем , откуда получаем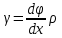 . .Из данной зависимости видно, что угол сдвига 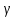 изменяется по радиусу вала по линейному закону. изменяется по радиусу вала по линейному закону. Деформация бруса при кручении характеризуется относительным углом закручивания 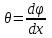 . Согласно закону Гука при сдвиге, имеем . Согласно закону Гука при сдвиге, имеем 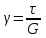 . Откуда получаем: . Откуда получаем: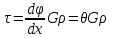 . .Из данной зависимости видно, что касательные напряжения изменяются по радиусу по линейному закону.  Рис. 20 При кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей - к крутящему моменту. Касательные напряжения перпендикулярны радиусам, проведенные через точки их действия (рис. 20). Крутящий момент 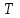 в сечении бруса определяется по уравнению в сечении бруса определяется по уравнению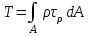 , ,где 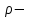 плечо элементарной силы. плечо элементарной силы. Подставляя значение касательного ускорения, получим 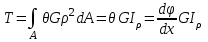 . .Элементарный угол закручивания 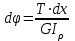 , а полный угол закручивания бруса , а полный угол закручивания бруса 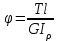 . .Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости: 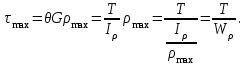 Таким образом, максимальное касательное напряжение в поперечном сечении бруса равно частному от деления крутящего момента на полярный момент сопротивления. 25 Построение эпюр поперечных сил и изгибающих моментов. При расчете балок на прочность необходимо знать характер изменения изгибающего момента и поперечной силы вдоль оси балки и знать положение опасного сечения. С этой целью строят эпюры поперечных сил и изгибающих моментов. Поперечная сила 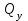 в сечении численно равна алгебраической сумме всех внешних сил справа или слева от сечения. в сечении численно равна алгебраической сумме всех внешних сил справа или слева от сечения.Изгибающий момент 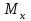 в сечении численно равен алгебраической сумме моментов внешних сил справа или слева от сечения. в сечении численно равен алгебраической сумме моментов внешних сил справа или слева от сечения.Если внешняя сила стремится повернуть отсеченную часть по часовой стрелке относительно рассматриваемого сечения, то поперечная сила положительна (рис. 24). Изгибающий момент будет положительным, если при действии момента внешних сил балка искривляется выпуклостью вниз (рис. 25).  Рис. 24  Рис. 25 Построение эпюр поперечных сил и изгибающих моментов рассмотрим на конкретном примере. Пусть на балку действует внешний изгибающий момент 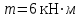 и внешняя сила и внешняя сила 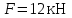 , , 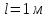 . Определим реакции в опорах . Определим реакции в опорах 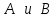 . Составим уравнения равновесия моментов всех внешних сил относительно опор . Составим уравнения равновесия моментов всех внешних сил относительно опор 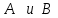 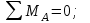 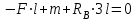 ; ;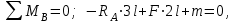 откуда 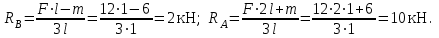  Рис. 26 Проведем сечения на каждом характерном участке и определим значения поперечной силы 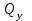 и изгибающего момента и изгибающего момента 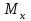 . .В сечении 1 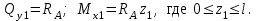 При 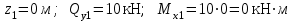 ; ;при 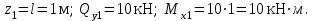 В сечении 2 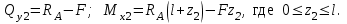 При 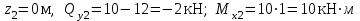 ; ;при 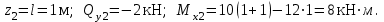 В сечении 3 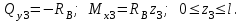 При 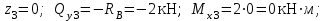 при 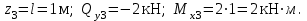 По полученным значениям строим эпюры поперечных сил и изгибающих моментов (рис. 26). 26-27 Основные понятия и определения. В отличие от деформации растяжения-сжатия и кручения изгиб представляет такую деформацию, при которой происходит искривление оси прямого бруса. Осью бруса называется геометрическое место точек центров тяжестей поперечных сечений бруса. Если в сечении бруса действует только один изгибающий момент, то изгиб называется чистым. Если в поперечных сечениях кроме изгибающего момента действует и поперечная сила, то изгиб называется поперечным. Брус, работающий на изгиб, называется балкой. Изгиб называется плоским, если ось балки после деформации остается плоской линией. В противном случае имеет место косой изгиб. В настоящем разделе рассматривается плоский прямой изгиб. Нормальные напряжения при чистом прямом изгибе. Так как нормальные напряжения зависят только от изгибающих моментов, то вывод формулы для вычисления 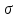 можно производить применительно к чистому изгибу. можно производить применительно к чистому изгибу.Статическая задача о плоском изгибе. Изгибающий момент в сечении представляет собой сумму моментов всех элементарных внутренних нормальных сил 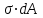 , возникающих на элементарных площадках поперечного сечения балки (рис. 22), относительно нейтральной оси , возникающих на элементарных площадках поперечного сечения балки (рис. 22), относительно нейтральной оси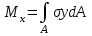 . . Рис. 22 Данное выражение представляет собой статическую сторону задачи о плоском изгибе. Однако его нельзя использовать для определения нормальных напряжений, так как неизвестен закон распределения напряжений по сечению. Геометрическая сторона задачи о плоском изгибе. Выделим двумя поперечными сечениями элемент балки длиной 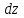 (рис. 23). Под нагрузкой нейтральная ось искривляется (радиус кривизны (рис. 23). Под нагрузкой нейтральная ось искривляется (радиус кривизны 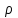 ), а сечения поворачиваются относительно своих нейтральных линий на угол ), а сечения поворачиваются относительно своих нейтральных линий на угол 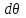 . Длина отрезка волокон нейтрального слоя при этом остается неизменной . Длина отрезка волокон нейтрального слоя при этом остается неизменной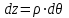 . . Рис. 23 Определим длину отрезка волокон, отстоящего от нейтрального слоя на расстоянии 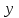 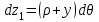 . .Относительное удлинение в этом случае будет 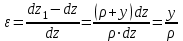 . .Зависимость 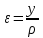 отражает геометрическую сторону задачи о плоском изгибе, из которой видно, что деформации продольных волокон изменяются по высоте сечения по линейному закону. отражает геометрическую сторону задачи о плоском изгибе, из которой видно, что деформации продольных волокон изменяются по высоте сечения по линейному закону. |
