Прикладная механика. Шпоры. 13 Геометрический метод сложения сил
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
Рис. 3.1Момент силы относительно оси Вращательный эффект действия силы на тело относительно оси определяется моментом силы относительно оси. Момент силы относительно оси находится иначе, чем момент силы относительно точки. Алгебраический момент силы относительно некоторой оси равен алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения плоскости с осью (рис. 3.2). Правило нахождения момента относительно оси: Необходимо спроецировать силу 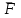 на плоскость перпендикулярную оси z. на плоскость перпендикулярную оси z.Подсчитать момент проекции силы 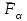 относительно точки пересечения оси с плоскостью относительно точки пересечения оси с плоскостью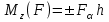 . (3.2) . (3.2)Момент силы относительно оси считается положительным, если при взгляде с положительного направления оси проекция силы  стремится повернуть тело против часовой стрелки. стремится повернуть тело против часовой стрелки.Аксиома: сила, параллельная оси, и сила пересекающая ось, не создают вращения относительно этой оси, то есть моменты таких сил относительно оси равны нулю.  Рис. 3.2 6 Способы задания движения точки Задать движение точки – значит задать ее положение относительно некоторой системы отсчета в любой момент времени. Естественный способ задания движения точки (рис. 4.1). Задать движение точки естественным образом – значит: а) задать траекторию движения точки в некоторой системе отсчета; б) на траектории выбрать начало О и положительное направление отсчета расстояний S=OM; в) указать закон движения точки S=f(t), а также начало отсчета времени t0. Функция S=f(t) должна быть однозначной, непрерывной, дифференцируемой. Закон движения точки может быть задан графически: кривой, отражающей зависимость S от t. Это графическое изображение закона движения точки называют графиком движения точки. 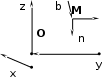 Рис. 4.1 На рис. 4.1 - ось, касательная к траектории движения точки, направленная в сторону положительного отсчета расстояния S; n – нормаль к траектории движения точки, направленная в сторону вогнутости траектории, b – бинормаль, перпендикулярна к первым двум так, чтобы она образовала с ними правую тройку. Эти оси называются естественными осями. Координатный способ. Положение точки в пространстве трех измерений можно однозначно определить, задав три ее координаты в некоторой системе отсчета. Задать движение точки в координатной форме – значит задать координаты этой точки как функции времени: x=f(t), y=f(t), z=f(t). Эти уравнения называются уравнениями движения точки. 7 Виды движения точки в зависимости от ускорения Прямолинейное движение. В этом случае траектория движения точки – прямая, причем точка движется вдоль этой прямой в одном направлении. Радиус кривизны прямой R равен бесконечности (прямую можно считать окружностью бесконечно большого радиуса). Тогда 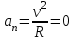 , поэтому может изменяться только алгебраическая величина скорости точки. Это изменение полностью характеризуется касательным ускорением , поэтому может изменяться только алгебраическая величина скорости точки. Это изменение полностью характеризуется касательным ускорением 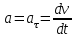 . .Равномерное криволинейное движение. Так как при равномерном движении точки модуль скорости остается постоянным, то есть v = const, тогда 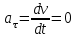 . Вектор полного ускорения а, следовательно, направлен по главной нормали в сторону вогнутости, модуль полного ускорения равен . Вектор полного ускорения а, следовательно, направлен по главной нормали в сторону вогнутости, модуль полного ускорения равен 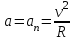 . .Равномерное прямолинейное движение. В этом случае 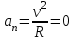 и и 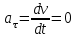 , а значит а = 0. Единственный вид движения, в котором ускорение точки все время остается равным нулю, - равномерное прямолинейное движение. , а значит а = 0. Единственный вид движения, в котором ускорение точки все время остается равным нулю, - равномерное прямолинейное движение.Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиной постоянной: 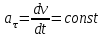 . Если при равномерном криволинейном движении точки модуль скорости возрастает, то движение называется равноускоренным, а если убывает – равнозамедленным. . Если при равномерном криволинейном движении точки модуль скорости возрастает, то движение называется равноускоренным, а если убывает – равнозамедленным.8 Вращение твердого тела вокруг неподвижной оси В  ращательным движением твердого тела называется движение, при котором две его точки А и В остаются неподвижными. Так как тело абсолютно твердое, то вместе с точками А и В будут неподвижны все точки, лежащие на прямой АВ. Эта прямая называется осью вращения (рис. 5.2). Все точки тела при вращательном движении описывают дуги окружностей с центрами в основаниях перпендикуляров, опущенных из этих точек на ось вращения. Проведем через ось вращения две полуплоскости, одну из которых зафиксируем, а другую свяжем с телом. Двугранный угол , угол поворота, между этими полуплоскостями будет однозначно определять положение тела. Задавая значение угла в каждый момент времени t, можно тем самым определить положение тела для любого t. Уравнение 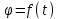 (5.3) (5.3)носит название закона вращательного движения тела. Функция (5.3) предполагается дважды дифференцируемой. Главными кинематическими характеристиками вращательного движения тела будут угловая скорость (с-1) и угловое ускорение (с-2). Пусть за некоторый промежуток времени 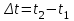 угол получит приращение угол получит приращение 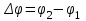 . Величина . Величина 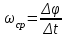 называется средней угловой скоростью тела. Предел, к которому стремится средняя угловая скорость при t0, называется угловой скоростью тела в данный момент времени t. называется средней угловой скоростью тела. Предел, к которому стремится средняя угловая скорость при t0, называется угловой скоростью тела в данный момент времени t.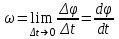 . (5.4) . (5.4)Если тело совершает вращательное движение по произвольному закону, то угловая скорость является функцией времени: 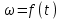 . .Пусть за некоторый промежуток времени 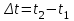 угловая скорость получила приращение угловая скорость получила приращение 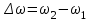 . Величина . Величина 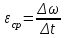 называется средним угловым ускорением. Предел, к которому стремится среднее ускорение при t 0, называется угловым ускорением в данный момент времени t. называется средним угловым ускорением. Предел, к которому стремится среднее ускорение при t 0, называется угловым ускорением в данный момент времени t.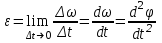 . (5.5) . (5.5)9 Понятие о плоскопараллельном движении твердого тела Движение твердого тела называется плоскопараллельным, если все точки тела перемещаются в плоскостях, параллельных некоторой фиксированной плоскости (основной плоскости). Пусть некоторое тело V совершает плоское движение, - основная плоскость (рис. 5.4). Из определения плоскопараллельного движения и свойств абсолютно твердого тела следует, что любой отрезок прямой АВ, перпендикулярный плоскости , будет совершать поступательное движение. То есть траектории, скорости и ускорения всех точек отрезка АВ будут одинаковы. Таким образом, движение каждой точки сечения s параллельного плоскости , определяет собой движение всех точек тела V, лежащих на отрезке перпендикулярном сечению в данной точке. П 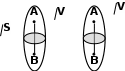 римерами плоскопараллельного движения являются: качение колеса по прямолинейному отрезку, так как все его точки перемещаются в плоскостях, параллельных плоскости, перпендикулярной оси колеса; частным случаем такого движения является вращение твердого тела вокруг неподвижной оси, в самом деле, все точки вращающегося тела движутся в плоскостях параллельных некоторой перпендикулярной оси вращения неподвижной плоскости. римерами плоскопараллельного движения являются: качение колеса по прямолинейному отрезку, так как все его точки перемещаются в плоскостях, параллельных плоскости, перпендикулярной оси колеса; частным случаем такого движения является вращение твердого тела вокруг неподвижной оси, в самом деле, все точки вращающегося тела движутся в плоскостях параллельных некоторой перпендикулярной оси вращения неподвижной плоскости.Рис. 5.4 Теорема о возможности представления плоскопараллельного движения в виде совокупности двух движений: поступательного и вращательного. Пусть некоторое тело совершает плоскопараллельное движение. Рассмотрим некоторое сечение этого тела параллельное основной плоскости. Произвольно выбранную точку сечения или плоскости, которой принадлежит сечение и которая неизменно связана с сечением, называют полюсом. Теорема. Всякое перемещение плоской фигуры в её плоскости может быть представлено в виде совокупности двух движений: поступательного и вращательного. Доказательство. П 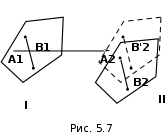 усть плоская фигура за некоторый промежуток времени t переместилась из положения I в положение II (рис. 5.7). Положение произвольно выбранного отрезка неизменно связанного с фигурой, определяет положение всей фигуры в любой момент времени. Выберем две произвольные точки фигуры А1 и В1 и примем точку А1 за полюс. Отрезок А1В1 через промежуток времени t займёт положение А2В2. Поступательным перемещением фигуры совместим точки А1 и А2. Точка В1 при этом займёт положение В'2, а сама фигура перейдёт в положение, отмеченное пунктиром. Поступательное перемещение фигуры определится вектором 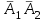 , и отрезок А1В1 будет параллелен отрезку А2В'2. Если теперь повернуть фигуру вокруг полюса А2 на угол В'2А2 В2, то отрезок А2В'2 займёт положение А2В2, а сама фигура - положение II, что и требовалось доказать. , и отрезок А1В1 будет параллелен отрезку А2В'2. Если теперь повернуть фигуру вокруг полюса А2 на угол В'2А2 В2, то отрезок А2В'2 займёт положение А2В2, а сама фигура - положение II, что и требовалось доказать.Теорема рассматривает не реальное, а возможное движение точки. Следствие из теоремы: Угловая скорость плоской фигуры не зависит от выбора полюса. 12-13 Кинетическая энергия Кроме количества движения основной мерой механического движения является кинетическая энергия. Кинетической энергией материальной точки называется скалярная величина, равная 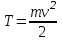 . (8.1) . (8.1)Кинетическая энергия – есть величина положительная при любых значениях скорости, при 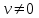 . Если . Если 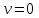 , то точка покоится относительно инерциальной системы отсчета и ее кинетическая энергия равна нулю. , то точка покоится относительно инерциальной системы отсчета и ее кинетическая энергия равна нулю.Теорема. Изменение кинетической энергии материальной точки за некоторый промежуток времени равно работе приложенной к точке силы за тот же промежуток времени. Доказательство: 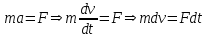 . .Умножим обе части скалярно на v, получим: 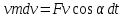 , где - угол между направлением вектора скорости и направлением линии действия силы. Полученную запись представим в виде , где - угол между направлением вектора скорости и направлением линии действия силы. Полученную запись представим в виде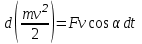 . .Правая часть этого равенства представляет собой элементарную работу силы F. Интегрируя полученное выражение в соответствующих пределах, получим: 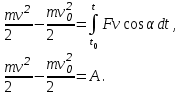 (8.2) (8.2) 14 Статические моменты сечения. Любое сечение бруса имеет определенную геометрическую форму и площадь (рис. 7). Выделим в сечение элементарную площадку 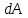 , положение которой определено координатами xи y. Статическим моментом сечения , положение которой определено координатами xи y. Статическим моментом сечения  называется интеграл по площади произведения элементарной называется интеграл по площади произведения элементарной площадки на расстояние до оси. Статические моменты сечения относительно осей xи y будут соответственно равны 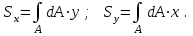  15 Определение центра тяжести сечения. Статические моменты сечения относительно осей проходящих через центр тяжести равны нулю, поэтому их используют для определения координат центров тяжести сечения. Для этого проводят вспомогательные оси xи y и координаты центра тяжести сечения определяют по зависимостям: 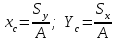 . .16 Моменты инерции сечения. Осевым моментом инерции сечения 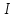 называется интеграл по площади произведения элементарной площадки на квадрат расстояния до оси. Осевые моменты инерции сечения относительно осей xи y будут соответственно равны называется интеграл по площади произведения элементарной площадки на квадрат расстояния до оси. Осевые моменты инерции сечения относительно осей xи y будут соответственно равны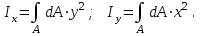 Полярным моментом инерции сечения 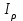 называется интеграл по площади произведения элементарной площадки на квадрат расстояния до начало координат. называется интеграл по площади произведения элементарной площадки на квадрат расстояния до начало координат.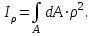 Учитывая, что 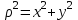 , получаем , получаем 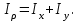 Полярный момент инерции сечения равен сумме осевых моментов инерции сечения. Центробежным моментом инерции сечения 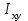 называется интеграл по площади произведения элементарной площадки на расстояния до осей. называется интеграл по площади произведения элементарной площадки на расстояния до осей.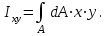 Если сечение имеет ось симметрии, то центробежный момент инерции сечения равен нулю. 17 Момент сопротивления сечения. Момент сопротивления сечения относительно оси представляет собой отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки сечения от этой же оси. 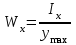 . .Момент сопротивления прямоугольного сечения, изображенного на рис. 8, относительно оси, проходящей через центр тяжести, равен 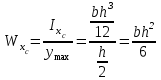 . .Полярный момент инерции представляет собой отношение полярного момента инерции к наибольшему расстоянию от центра тяжести сечения до наиболее удаленной точки сечения 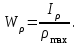 18. Диаграмма растяжения. Основные механические свойства материала. Необходимые сведения о различных механических свойствах материала получают экспериментальным путем. Самым распространенным является испытание на растяжение. Испытание производят на разрывной машине стандартного образца. При нагружении снимают показание растягивающей силы и длину образца. Затем строится условная диаграмма растяжения в координатах 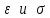 . Напряжение в сечении определяют по зависимости: . Напряжение в сечении определяют по зависимости: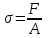 , ,где 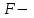 сила нагружения; сила нагружения;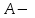 площадь поперечного сечения образца. площадь поперечного сечения образца.Относительная линейная деформация определяется из выражения 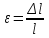 , , где 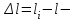 относительное удлинение образца; относительное удлинение образца;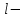 исходная длина образца; исходная длина образца;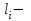 длина образца в данный момент отсчета. длина образца в данный момент отсчета.Диаграмма растяжения для пластичных материалов имеет вид, показанный на рис. 6. На диаграмме растяжения можно выделить четыре характерные участка. Участок 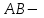 участок пропорциональности. На этом участке выполняется закон Гука участок пропорциональности. На этом участке выполняется закон Гука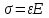 . . Рис. 6 Участок 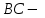 площадка текучести. На этом участке происходит удлинение образца без изменения нагрузки. Напряжение, при котором происходит течение образца, называется пределом текучести и обозначается площадка текучести. На этом участке происходит удлинение образца без изменения нагрузки. Напряжение, при котором происходит течение образца, называется пределом текучести и обозначается 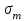 . .Участок 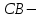 участок упрочнения. На этом участке для дальнейшего удлинения образца необходимо увеличить нагрузку. участок упрочнения. На этом участке для дальнейшего удлинения образца необходимо увеличить нагрузку.В точке 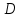 происходит образование шейки и на участке происходит образование шейки и на участке 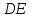 происходит местное удлинение образца. Напряжение, при котором образуется шейка, называется пределом прочности и обозначается происходит местное удлинение образца. Напряжение, при котором образуется шейка, называется пределом прочности и обозначается 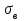 . . |
