вопросы. вопросы надежности. 1 Анализ задач исследования надежности
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
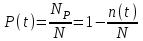 , (1) , (1)где NР - число работоспособных изделий к концу времени t испытаний или эксплуатации; N - число изделий, поставленных на испытания или эксплуатацию; n(t) - число изделий, отказавших к концу времени t испытаний или эксплуатации. Так как безотказная работа и отказ - взаимно противоположные события, то оценку вероятности отказа определяют по формуле 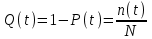 , (2) , (2)Распределение отказов во времени характеризуется функцией плотности распределения f(t) наработки до отказа. Статистическая оценка плотности распределения имеет вид: 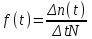 , (3) , (3)где Δn(t) - приращение числа отказавших изделий за время Δt. Вероятность отказов и безотказной работы в функции плотности распределения выразятся зависимостями: 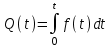 , (4) , (4)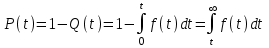 , (5) , (5)Интенсивность отказов в статистической трактовке определяется соотношением: 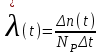 , (6) , (6)В вероятностном смысле интенсивность отказов выразится зависимостью: 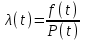 , (7) , (7)Отсюда вероятность безотказной работы после преобразований определится по формуле: 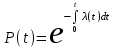 , (8) , (8)Это соотношение является одним из основных уравнений теории надежности. 20 Показатели безотказности В рассматриваемых способах оценки вероятности безотказной работы до первого отказа отказы не различаются по тяжести их последствий. В большинстве случаев при проектировании изделий необходимо установить критерий отказа изделия: по экономическим последствиям восстановления его работоспособности, исчерпанию ресурса и другим характеристикам. Критерием отказа называют признак или совокупность признаков неработоспособного состояния объекта, установленных в нормативно-технической или конструкторской документации. Средняя наработка на отказ - это отношение наработки восстанавливаемого объекта к математическому ожиданию числа отказов в течение этой наработки. Статистическую оценку среднего значения наработки на отказ 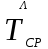 вычисляют как отношение суммарной наработки за рассматриваемый период испытаний или эксплуатации объектов к суммарному числу отказов этих объектов за тот же период: вычисляют как отношение суммарной наработки за рассматриваемый период испытаний или эксплуатации объектов к суммарному числу отказов этих объектов за тот же период: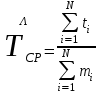 , (8) , (8)Средняя наработка до отказа - это математическое ожидание наработки объекта до первого отказа. Среднюю наработку до отказа определяют по формулам: для непрерывной функции надежности 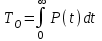 , (9) , (9)для дискретной функции надежности: 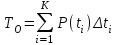 , (10) , (10)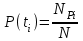 , (11) , (11)где Npi - число работоспособных объектов на интервале наработки ti+1-ti, N - общее число объектов, поставленных на испытания или в эксплуатацию; Δti=ti+1-ti, К - общее число рассматриваемых интервалов наработки эмпирической функции надежности. Средняя наработка между отказами - это математическое ожидание наработки объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа. Статистическую оценку среднего значения наработки между отказами вычисляют как отношение суммарной наработки объекта между отказами за рассматриваемый период испытаний или эксплуатации к числу отказов этого(их) объекта(ов) за тот же период: 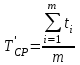 , (12) , (12)Статистическую оценку параметра потока отказов вычисляют как отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки 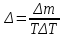 , (13) , (13)где Δm - среднее число отказов восстанавливаемого объекта на интервале ΔT наработки; T-рассматриваемый период наработки. Перечисленные показатели безотказности в зависимости от целей исследования определяют на различных стадиях работы объекта. Так, наработку на отказ в период приработки объекта определяют для выявления ранних отказов с целью принятия необходимых мер по совершенствованию конструкции и технологии изготовления, исключающих причины появления подобных отказов при серийном производстве этих объектов. 21Функции распределения и основные свойства Отказы, возникающие в процессе испытаний или эксплуатации, могут быть вызваны неблагоприятным сочетанием различных факторов -рассеянием действующих нагрузок, отклонением от номинального значения физических характеристик материалов, неблагоприятным сочетанием допусков в местах сопряжения и т.п. Поэтому в расчетах надежности различные параметры рассматриваются как случайные величины, которые могут принимать то или иное значение, неизвестное заранее. Различают случайные величины прерывного (дискретного) и непрерывного типов. Условимся случайные величины в дальнейшем обозначать большими буквами, а их возможные значения - соответствующими малыми. Для каждого числа х в диапазоне изменения случайной величины X существует определенная вероятность Р(Х<х) того, что X не превышает значения х. Вероятность этого события называют функцией распределения: 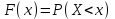 , (14) , (14)Функция распределения - универсальная характеристика, так как она является функцией как непрерывных, так и дискретных случайных величин. Функция F(x) относится к неубывающим функциям - она монотонно возрастает при непрерывных процессах и ступенчато возрастает при дискретных процессах (рисунок 1). 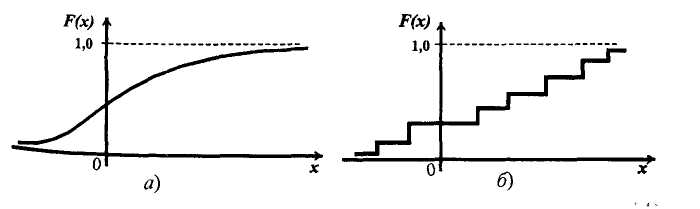 Рисунок 1 - Функция распределения: а - для непрерывных процессов; б - для дискретных процессов Основными свойствами функции распределения являются: Функция изменяется от 0 до 1 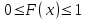 , (15) , (15)На минус бесконечности функция равна нулю 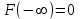 , (16) , (16)На плюс бесконечности функция равна единице 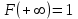 , (17) , (17)22 Плотность распределения и основные свойства Производная от функции распределения по текущей переменной называется плотностью распределения, которая характеризует частоту повторений данного значения случайной величины. В теории надежности величину f(x) называют плотностью вероятности: 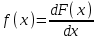 , (18) , (18)Основные свойства плотности распределения: Плотность распределения есть неотрицательная функция своего аргумента: 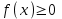 , (19) , (19)Интеграл в бесконечных пределах от плотности распределения равен единице: 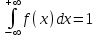 , (20) , (20)Плотность распределения существует только для непрерывных случайных величин. Графическое изображение показано на рисунке 2. 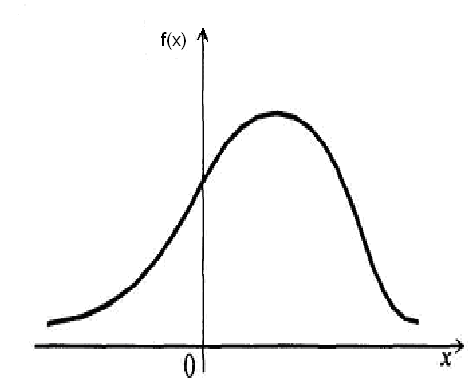 Рисунок 2 Плотность распределения 23 Математическое ожидание, дисперсия В ряде случаев в качестве характеристик распределения случайных величин достаточно использовать некоторые числовые величины, среди которых в теории надежности наиболее употребительными являются математическое ожидание (среднее значение), мода и медиана (характеризуют положение центров группирования случайных величин на числовой оси), дисперсия, среднее квадратическое отклонение и коэффициент вариации (характеризуют рассеяние случайной величины). Значения характеристик, полученные по результатам испытаний или эксплуатации, называют статистическими оценками. Характеристики распределения используют для прогнозирования надежности. Для дискретных случайных величин математическое ожидание Мх равно сумме произведения всех возможных значений X на вероятности этих значений: 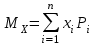 , (21) , (21)Математическое ожидание для непрерывной случайной величины выражается интегралом в бесконечных пределах от произведения непрерывно изменяющихся возможных значений случайной величины на плотность распределения 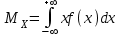 , (22) , (22)Математическое ожидание случайной величины непосредственно связано со средним значением. При неограниченном увеличении числа опытов среднее арифметическое значение величины х приближается к математическому ожиданию и называется оценкой среднего значения: 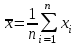 , (23) , (23)где n - общее число опытов; хi - текущее значение случайной величины. Дисперсией (DX) случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания. Для дискретной случайной величины дисперсия равна: 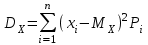 , (24) , (24)Для непрерывной случайной величины дисперсия определяется из выражения 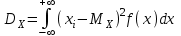 , (25) , (25)Оценка дисперсии случайной величины: 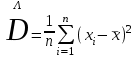 , (26) , (26)Дисперсия случайной величины является характеристикой рассеяния - разбросанности значений случайной величины около ее математического ожидания. Размерность дисперсии соответствует квадрату размерности случайной величины. Для наглядности в качестве характеристики рассеяния удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такой характеристикой может быть среднее квадратическое отклонение σХ, которое определяется как корень квадратный из дисперсии: 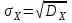 , (27) , (27)Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен: 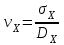 , (28) , (28)24 Мода, медиана, квантиль Модой случайной величины называют ее наиболее вероятное значение или то ее значение, при котором плотность вероятности максимальна. Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам. Квантиль - значение случайной величины, соответствующее заданной вероятности. Квантиль, соответствующую вероятности 0,5, называют медианой. Аналогично предыдущим характеристикам понятия моды и медианы даны в статистической трактовке. Для симметричного модального (т.е. имеющего один максимум) распределения математическое ожидание, мода и медиана совпадают. 25 Показатели безотказности и ремонтопригодности Любая система характеризуется безотказностью и ремонтопригодностью. В качестве основной характеристики безотказности системы служит функция надежности, которая представляет собой вероятность безотказной работы в течение некоторого времени t. Пусть система состоит из n элементов, функции надежности которых обозначим через p1(t), p2(t), ..., pn(t). Так как элементы, входящие в состав системы, являются независимыми, то вероятность безотказной работы системы определяется как произведение вероятностей составляющих ее элементов: 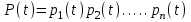 , (29) , (29)В частном случае, когда функции надежности составляющих элементов имеют экспоненциальное распределение с постоянными интенсивностями отказов, функция надежности системы определяется по формуле: 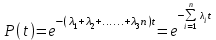 , (30) , (30)Одной из важнейших характеристик безотказности системы является среднее время жизни, которое вычисляют, используя выражение 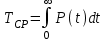 , (31) , (31)Для случая экспоненциального распределения среднее время жизни системы равно: 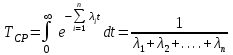 , , (32) (32)Среднее время жизни системы или наработку на отказ по результатам статистических данных вычисляют по формуле: 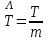 , (33) , (33)где Т - суммарная наработка системы, полученная по результатам испытаний или эксплуатации; m - суммарное число отказов, зафиксированное в процессе испытаний или эксплуатации. В качестве основной характеристики ремонтопригодности служит среднее время восстановления системы, которое находят из соотношения вида: 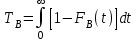 , (34) , (34)где FB(t) - функция распределения времени восстановления. Среднее время восстановления системы по результатам испытаний или эксплуатации определяют из зависимости:  , (35) , (35)где mi - число отказов i-го элемента; tBi- время восстановления i-го отказа. 26 Комплексные показатели и их характеристика Любая система характеризуется комплексными показателями надежности, такими, как коэффициенты: готовности КГ, технического использования КТ.И и оперативной готовности КО.Г. Коэффициент оперативной готовности характеризует надежность системы, необходимость применения которой возникает в произвольный момент времени (кроме планируемых периодов, в течение которых применение системы по назначению не предусматривается). Значение коэффициента оперативной готовности определяют из выражения: 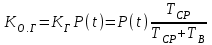 , (36) , (36)27 Среднее время восстановления и вероятность восстановления В теории надежности для изделий машиностроения чаще всего используют два показателя ремонтопригодности - среднее время восстановления и вероятность восстановления. Среднее время восстановления - математическое ожидание времени восстановления объекта. Статистическую оценку этого параметра определяют по формуле: 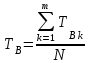 , (37) , (37)где ТВk - время восстановления k - го отказа объекта; m - число отказов объекта за заданный срок испытаний или эксплуатации. Вероятность восстановления работоспособного состояния - это вероятность того, что объект будет восстановлен в заданное время tв. Для большинства изделий машиностроения вероятность восстановления подчиняется закону Пуассона: 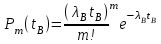 , (38) , (38)где λВ - интенсивность восстановления, m - число восстановлений (отказов). 28 Комплексные показатели надежности К комплексным показателям относятся коэффициенты: готовности, технического использования и оперативной готовности. Коэффициент готовности (КГ) - вероятность того, что объект окажется работоспособным в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. По КГ судят о надежности объекта на определенном интервале эксплуатации, поэтому при нормировании этого показателя необходимо в нормативно-технической документации (НТД) указывать интервал эксплуатации объекта, на котором следует оценивать КГ. Среднее статистическое значение КГ определяют по формуле 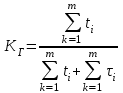 , (39) , (39)где ti - суммарная наработка i-го объекта в заданном интервале эксплуатации; τi- - суммарное время восстановления i-го объекта за тот же период эксплуатации; N - число наблюдаемых объектов в заданном интервале эксплуатации. Если на заданном интервале эксплуатации определены среднее значение наработки на отказ и среднее время восстановления объекта после отказа, то: 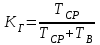 , (40) , (40)где ТСР - среднее значение наработки на отказ, ТВ - среднее время восстановления объекта после отказа. Коэффициент технического использования - отношение математического ожидания наработки Т объекта за некоторый период эксплуатации к сумме математических ожиданий наработки, продолжительности технических обслуживании τ ТО, плановых ремонтов τР и внеплановых восстановлений τВ за тот же период эксплуатации. Рассчитывают КТИ по формуле: 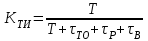 , (41) , (41)Коэффициент оперативной готовности — вероятность того, что объект окажется работоспособным в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и, начиная с этого момента, объект будет работать безотказно в течение заданного интервала времени. Численное значение коэффициента оперативной готовности определяют из выражения |
