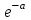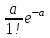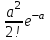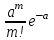вопросы. вопросы надежности. 1 Анализ задач исследования надежности
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
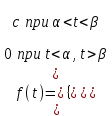 , (119) , (119)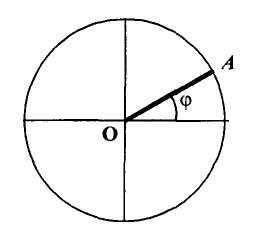 Рисунок 13 Вертикально поставленное симметричное колесо 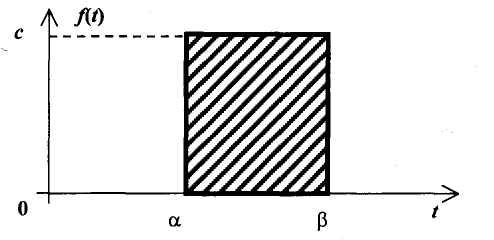 Рисунок 14 Плотность распределения для равномерного закона Так как площадь, ограниченная кривой распределения, равна едини- це, т.е. с( β-α )=1, то с = 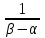 . .Тогда плотность распределения имеет вид: 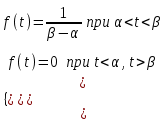 , (120) , (120)Формула (120) выражает закон равномерного распределения плотности на участке (α, β). Функция распределения для равномерного закона (рисунок 15) определяется соотношением вида: 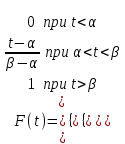 , (121) , (121)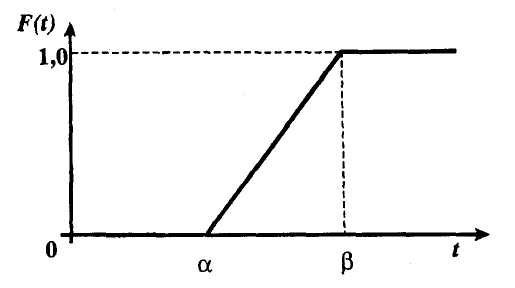 Рисунок 15 Функция распределения для равномерного закона Определим числовые характеристики случайной величины Т, подчиненной закону равномерной плотности на участке от α до β. Математическое ожидание величины Т равно: 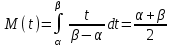 , (122) , (122)Дисперсия определяется по формуле: 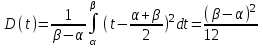 , (123) , (123)откуда среднее квадратичное отклонение равно: 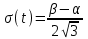 , (124) , (124)Вероятность попадания случайной величины Т, распределенной по закону равномерной плотности, на участок (α, β) определяется по соотношению вида (рисунок 16) 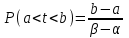 , (125) , (125)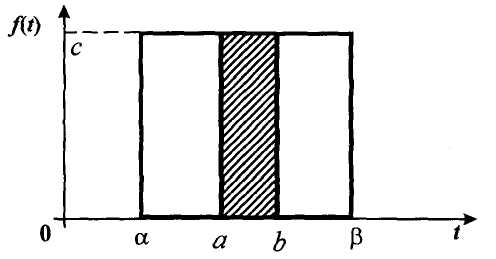 Рисунок 16 График закона равномерной плотности при попадании случайной величины на участок (a, b) 17 Закон Пуассона случайной величины Во многих задачах практики часто приходится встречаться со случайными величинами, которые в процессе испытаний принимают целые неотрицательные числа 0, 1, 2,..., m, причем последовательность этих чисел теоретически неограничена. Случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой 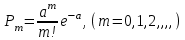 , (126) , (126)где а - некоторая положительная величина, называемая параметром закона Пуассона. Ряд распределения случайной величины X, распределенной по закону Пуассона, имеет вид:
Графически многоугольник распределения случайной величины, распределенной по закону Пуассона, для различных значений а представлен на рисунке 17. 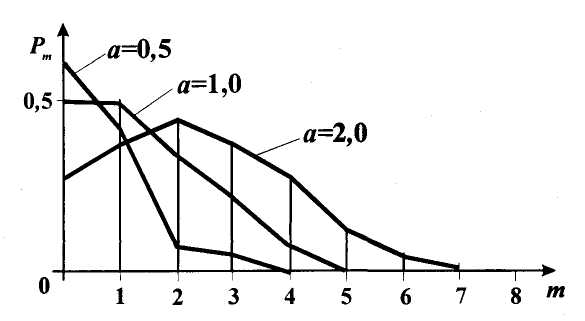 Рисунок 17 Распределение по закону Пуассона Математическое ожидание 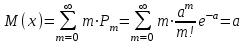 , (127) , (127)Таким образом, параметр а представляет собой не что иное, как математическое ожидание случайной величины X. Дисперсия случайной величины для закона Пуассона также равна параметру 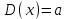 , (128) , (128)Это свойство распределения Пуассона часто применяется на практике для решения вопроса: правдоподобна ли гипотеза о том, что случайная величина Х распределена по закону Пуассона. Одним из наиболее важных дискретных распределений является биномиальное. Это двухпараметрическое распределение с параметрами n и р нашло практическое применение при оценке надежности изделий, работающих в циклическом режиме, где n - любое натуральное число, а р — любое вещественное число от 0 до 1. Важно отметить, что и должно быть либо фиксированным в начале испытаний, либо независимым от результатов каждого испытания. Если проводят n независимых испытаний с вероятностью q отказа и вероятностью р успеха в каждом из них, то вероятность появления m отказов подчиняется биномиальному распределению и определяется по формуле: 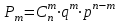 , (129) , (129)где p=1-q 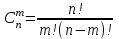 Соответственно вероятность появления k успехов вычисляют, используя соотношение: 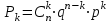 , (130) , (130) Математическое ожидание числа отказов равно 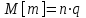 , (131) , (131)а числа успехов соответственно:  , (132) , (132)Дисперсия числа отказов (успехов) одинакова и равна 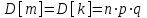 , (133) , (133)18 Закон биномиального распределения случайной величины Закон биномиального распределения нашел широкое применение в технике при оценке надежности изделий, работающих в циклическом режиме, а также в вопросах теории стрельбы из артиллерийских орудий. Для оценки вероятности появления случайного события не менее m' раз используют соотношение: 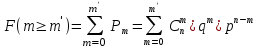 , (134) , (134)где р - вероятность появления случайного события в одном испытании (опыте), q = 1 - р - вероятность непоявления случайного события в одном испытании (опыте). В случае большого числа опытов и соответственно большого числа появлений интересующего нас события биномиальное распределение приближается к нормальному и тогда вместо формулы (134) можно воспользоваться соотношением: 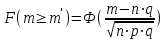 , (135) , (135)где Ф(UP) - функция нормального распределения берется из приложения. 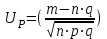 - квантиль функции нормального распределения - квантиль функции нормального распределенияВ практических вопросах теории надежности часто встречаются задачи, связанные с выбраковкой деталей из больших партий. Пусть проводится случайная выборка объемом n изделий, причем известно, что объем партии проводимой выборки составляет N изделий, в которой содержится М бракованных изделий. Ставится задача найти вероятность того, что в выборке объемом n изделий окажется m дефектных. Особенно вызывает интерес, когда М значительно меньше N, а также n мало по сравнению с N. В этом случае m может принимать целые неотрицательные числа 0, 1, 2,..., min (M, n). Для гипергеометрического распределения вероятность появления рассматриваемого события (в нашем случае появления m дефектных изделий в выборке) определяются по формуле: 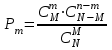 , (136) , (136)Математическое ожидание числа дефектных изделий равно: 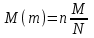 , (137) , (137)Дисперсия числа дефектных изделий находится из выражения вида: 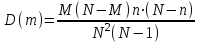 , (138) , (138)Дискретная функция распределения описывается соотношением: 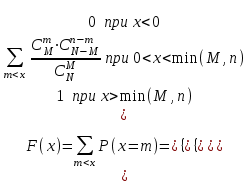 , (139) , (139)В соотношении (139) биномиальные коэффициенты вычисляют используя выражения: 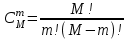 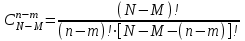 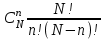 19 Задачи исследования при проектировании технической системы Для ряда изделий и сооружений проблема обеспечения надежности решается без использования методов теории надежности. Промышленные и жилые здания, мосты, плотины и другие сооружения проектируются с учетом эксплуатационных нагрузок и изменений во времени свойств конструкционных материалов. Установленные для различных видов сооружений нормы прочности и другие строительные и проектные нормы обеспечивают практическое отсутствие отказов в течение всего срока службы. При проектировании технической системы в основу исследований ставятся следующие задачи: - задача обоснования требований по надежности к системе и ее основным составным частям. Выбор путей их достижения с учетом ограничений, связанных с научно-техническими достижениями и ресурсами, выделяемыми на создание системы. - задача синтеза требуемой надежности системы в рамках принятых концепций построения системы с учетом упомянутых выше ограничений. - задача анализа надежности системы и ее основных составных частей с помощью расчетных оценок показателей надежности для различных вариантов технических решений по обеспечению надежности системы. - задачи распределения выделенных ресурсов на обеспечение надежности, реализуемых при создании, эксплуатации и применении системы по назначению. К их числу относят задачи обоснования программ обеспечения надежности, программ испытаний, выбора эффективных средств контроля качества изделия, поддержания надежности системы в процессе эксплуатации и др. Все перечисленные задачи могут успешно решаться при использовании различных количественных методов исследования надежности, которыми располагает теория надежности. Необходимо помнить, что теория надежности - наука экспериментальная, которая базируется на результатах испытаний или эксплуатации ранее созданной техники, поэтому количественный анализ надежности не исключает возможность ошибок, однако нельзя пренебрегать и количественной оценкой надежности при обосновании проектных решений. 20 Проектный расчет вероятностной функции надежности систем с последовательным соединением элементов Последовательным, в смысле надежности, называют такое соединение элементов в системе, при котором отказ хотя бы одного элемента приводит к отказу всей системы. Большинство механических, электромеханических, гидромеханических, оптико-механических и других средств представляют собой системы с последовательным соединением элементов. Высокий уровень надежности таких систем достигается за счет использования надежных элементов, правильного назначения периодичности технического обслуживания, обеспечения быстрого восстановления или замены отказавших элементов в процессе эксплуатации. К последовательному соединению элементов относятся также некоторые резервные элементы, когда отказ резервного элемента приводит к отказу системы. На практике это происходит, например, в электронной аппаратуре при коротком замыкании, в гидравлической и пневматической системах при разрыве трубопроводов и выходе из строя клапанов и т.п. Последовательные системы могут состоять из невосстанавливаемых и восстанавливаемых элементов. Для системы, состоящей из n последовательно соединенных невосстанавливаемых элементов, случайная наработка до отказа системы равна минимальному значению случайных наработок ее элементов. Если элементы являются независимыми и известны вероятности безотказной работы каждого элемента за заданное время t0, то вероятность безотказной работы системы за заданное время t0 будет равна: 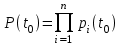 , (165) , (165)21Резервирование элементов Одним из способов повышения надежности систем является резервирование элементов, которое широко используется на стадии проектирования. Система с параллельным соединением элементов построена таким образом, что отказ ее происходит лишь в случае отказа всех элементов, т.е. система исправна, если исправен хотя бы один элемент. При разработке технических систем в зависимости от выполняемой задачи применяют нагруженное (горячее) и ненагруженное (холодное) резервирование. Горячее резервирование применяют тогда, когда не допускается перерыва времени на переключение отказавшего элемента на резервный с целью выполнения задачи в установленное время. Чаще всего горячему резервированию подвергаются отдельные элементы или отдельные каналы. Холодное резервирование применяют тогда, когда требуется увеличение ресурса работы элемента и допускается время на переключение отказавшего элемента на резервный. 22 Параллельное резервирование Существуют технические системы с частично параллельным резервированием. Это такие системы, которые оказываются работоспособными в случае отказа нескольких элементов. Если система представляет собой ряд нагруженных параллельно соединенных n элементов, изображенных на рисунке 19, то вероятность отказа системы равна: 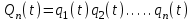 , (180) , (180)При условии одинаковой ненадежности элементов выражение принимает вид: 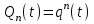 , (181) , (181)где n - число параллельно соединенных элементов. 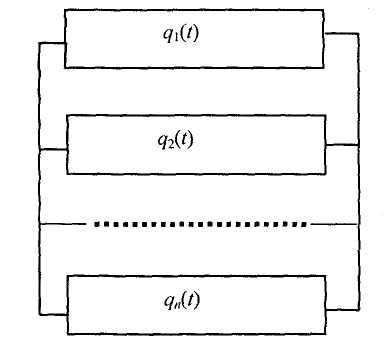 Рисунок 19 Структурная схема надежности системы с параллельным соединением элементов Тогда вероятность безотказной работы системы будет соответственно равна: 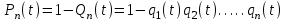 , (182) , (182)При  : :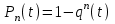 , (183) , (183)Формула (181) проста и удобна в практическом применении. Если, например, известна вероятность отказа элемента q(t) и требуется определить такое число резервных элементов, при котором ненадежность Qn(t) не будет превосходить заданной величины Q(t), т.е. 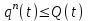 , (184) , (184)Тогда из неравенства (184) получим: 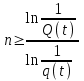 , (185) , (185)Если же, наоборот, задавшись числом резервных элементов, определять какой должна быть надежность каждого из них, то получим: 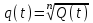 , (186) , (186)Среднее время безотказной работы резервной группы из n элементов при равнонадежных элементах: 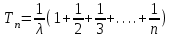 , (187) , (187)В случае ненагруженного (холодного) резерва среднее время резервной группы равно: 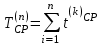 , (188) , (188)где 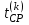 - среднее время жизни k-го элемента. - среднее время жизни k-го элемента.В частности, если все элементы равнонадежны, то: 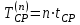 , (189) , (189)Тогда надежность систем при холодном резервировании определится соответственно по формуле: 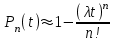 , (190) , (190)Если в системе (рисунок 20)  элементов не дублированы, a b элементов дублированы, то надежность системы: элементов не дублированы, a b элементов дублированы, то надежность системы: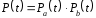 , (191) , (191)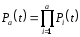 , (192) , (192)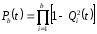 , (193) , (193)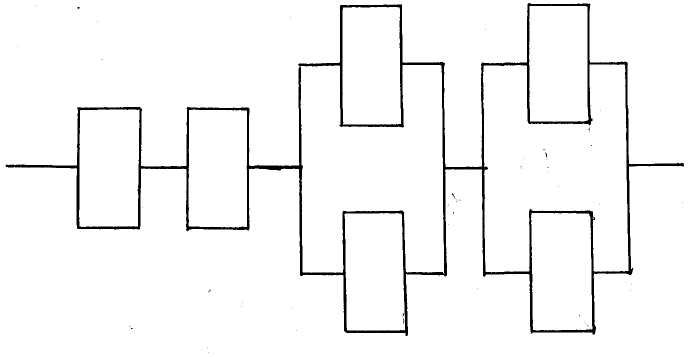 Рисунок 20 Частично зарезервированная система 23 Резервирование с замещением При резервировании замещением резервные элементы включаются только при отказе основных элементов (рисунок 21,22,23,24). Это включение может производиться автоматически или вручную. 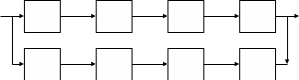 Рисунок 21 - Дублированная система с постоянным резервом          |