вопросы. вопросы надежности. 1 Анализ задач исследования надежности
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
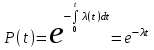 , (71) , (71)где е - основание натурального логарифма; λ - интенсивность отказов (параметр распределения). Если, как обычно, λ<<0,1, то формула вероятности безотказной работы упрощается в результате разложения в ряд и принимает вид: 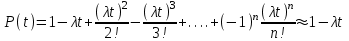 , (72) , (72)Плотность распределения экспоненциального закона (рисунок 6) описывается соотношением: 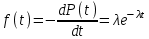 , (73) , (73) Рисунок 6 График плотности экспоненциального распределения Функция распределения выражается зависимостью:  , (74) , (74)Математическое ожидание, дисперсия и среднее квадратическое отклонение этого закона соответственно равны:  , , 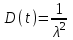 , , 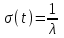 (75) (75)10 Нормальный закон распределения Нормальный закон распределения часто называют законом Гаусса. Этот закон занимает важное место, и наиболее часто используется на практике по сравнению с другими законами распределения. Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надежности его используют для описания постепенных отказов, когда распределение времени безотказной работы в начале имеет низкую плотность, затем максимальную и далее плотность снижается, т.е. нормальным распределением описывают наработки на отказ элементов и систем вследствие их износа и старения. Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы. Нормальный закон распределения описывается плотностью вероятности: 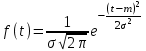 , (76) , (76)где m и 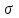 - параметры распределения, определяемые по результатам испытаний. - параметры распределения, определяемые по результатам испытаний. Кривая плотности распределения имеет вид колоколообразной формы (рисунок 7).  а) б) Рисунок 7 Кривая плотности вероятности (а) функции надежности (б) нормального распределения Параметр m представляет собой среднее значение исследуемой случайной величины 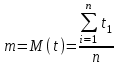 , (77) , (77)параметр 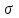 - среднее квадратическое отклонение исследуемой случайной величины, оцениваемое по формуле: - среднее квадратическое отклонение исследуемой случайной величины, оцениваемое по формуле: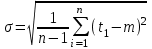 , (78) , (78)Функция распределения имеет вид: 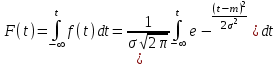 , (79) , (79)Функция надежности противоположна функции распределения: 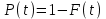 . (80) . (80)Вычисление интегралов заменяют использованием таблиц нормального распределения, при котором m = 0 и 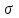 = 1. Для этого распределения функция плотности вероятности имеет одну переменную t и выражается зависимостью: = 1. Для этого распределения функция плотности вероятности имеет одну переменную t и выражается зависимостью: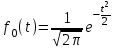 , (81) , (81)Величина t является центрированной (так как m = 0) и нормированной (так как 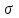 = 1). = 1).Функция распределения соответственно запишется в виде: 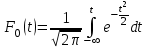 , (82) , (82)Из этого уравнения следует, что F0(t)+ F0(-t)=1 или 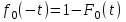 При использовании таблицей 1 приложения следует в формулу (82) вместо t подставить значение: 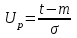 , (83) , (83)при этом 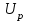 , называют квантилью нормированного нормального распределения. , называют квантилью нормированного нормального распределения.Нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий. Помимо задачи оценки вероятности безотказной работы за данное время или за данную наработку встречается обратная задача - определение наработки, соответствующей заданной вероятности безотказной работы. Значения этой наработки (времени) определяют с помощью квантили нормального распределения:  (84) (84)Значения квантилей 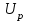 в зависимости от требуемой вероятности в зависимости от требуемой вероятностиданы в таблице 1 приложения. В работах по надежности часто вместо интегральной функции распределения 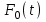 используют функцию Лапласа: используют функцию Лапласа: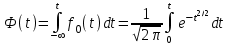 , (85) , (85)Очевидно, что: 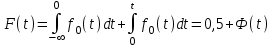 , (86) , (86)Вероятности отказа и безотказной работы, выраженные через функцию Лапласа: 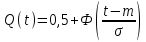 , (87) , (87)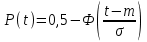 Вероятность попадания случайной величины в интервал 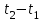 вычисляют по формуле: вычисляют по формуле: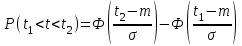 , (88) , (88) Табличный интеграл Ф(t) равен площади кривой, заключенной между осью симметрии и ординатой, соответствующей значению t, и определяет вероятность того, что значение случайной величины находится в пределах от 0 до t. 11 Закон распределения Вейбулла Среди непрерывных распределений закон Вейбулла занимает одно из наиболее часто применяемых в оценке надежности технических систем по результатам испытаний и эксплуатации. Это распределение Вейбулл использовал при описании разбросов усталостной прочности стали, пределов ее упругости, размеров частиц копоти и др. В последнее время закон распределения Вейбулла нашел применение при описании надежности сложных технических систем, а также при изучении разбросов в сроках службы изделий различного назначения. Его используют для оценки надежности деталей и узлов машин, а также для оценки надежности машин в процессе их приработки. Такое широкое использование данного закона объясняется тем, что он представляет собой двухпараметрическое распределение. Плотность распределения описывается зависимостью: 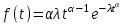 , (89) , (89)где α - параметр формы кривой распределения; λ - параметр масштаба. График плотности распределения дан на рисунке 8. Экспоненциальное распределение является частным случаем распределения Вейбулла при α = 1. Функция распределения описывается соотношением:  , (90) , (90)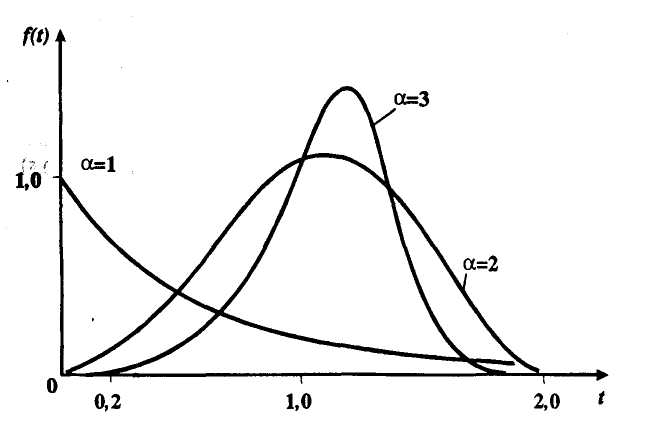 Рисунок 8 Плотность распределения Вейбулла для λ = 1 Функция надежности - величина, противоположная функции распределения:  , (91) , (91)Математическое ожидание и среднее квадратическое отклонение соответственно равны: 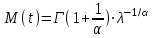 , , (92) 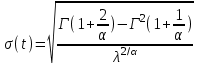 где Г(α) - гамма-функция. Гамма-функция для непрерывной величины описывается интегралом  , (93) , (93)Для вычисления значений функции Г(n+α), где n — целое число, а α - дробное при 2 ≤ n≤ 6, рекомендуется применять формулу: 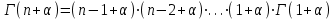 , (94) , (94) При n > 6 значения Г(n + α) можно находить по формуле: 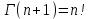 , (95) , (95)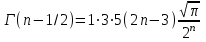 , (96) , (96)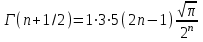 , (97) , (97)Широкое применение закона распределения Вейбулла объясняется тем, что этот закон, обобщая экспоненциальное распределение, содержит дополнительный параметр α. Подбирая нужным образом параметры α и λ, можно получить лучшее соответствие расчетных значений опытным данным по сравнению с экспоненциальным законом, который является однопараметрическим (параметр λ). Так, для изделий, у которых имеются скрытые дефекты, но некоторые длительное время не стареют, опасность отказа имеет наибольшее значение в начальный период, а потом быстро падает. Функция надежности для такого изделия хорошо описывается законом Вейбулла с параметром α<1. Наоборот, если изделие хорошо контролируется при изготовлении и почти не имеет скрытых дефектов, но подвергается быстрому старению, то функция надежности описывается законом Вейбулла с параметром α>1. При α=3,3 распределение Вейбулла близко к нормальному. 12 Логарифмически нормальный закон распределения Логарифмически нормальное распределение является двухпараметрическим распределением случайной величины, логарифм которой распределен по нормальному закону. Как распределение положительных величин, оно несколько точнее, чем нормальное. В теории надежности такое распределение используют для описания наработки на отказ деталей и узлов в период наступления усталости материала, а также процессов восстановления, износовых отказов, наработки на отказ подшипников качения и наработки между отказами сложных технических систем. Плотность распределения описывается зависимостью: 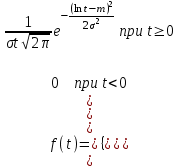 , (98) , (98)Параметры m и σ оценивают по результатам испытаний с помощью формул:  , (99) , (99)где ti - наработка до отказа i-го изделия; n - число изделий, поставленных на испытания 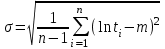 , (100) , (100)Функция распределения имеет вид:   , (101) , (101)Или: 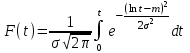 , (102) , (102)Вероятность безотказной работы можно определить по таблицам для нормального распределения в зависимости от значения квантили:  , (103) , (103)Математическое ожидание и среднее квадратическое отклонение наработки на отказ соответственно равны: 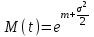 ; ; 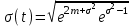 , (104) , (104)Коэффициент вариации равен: 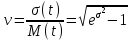 , (105) , (105)При ν≤0,3 полагают, что ν=σ, при этом ошибка не более 1 %. Кривые плотности распределения изображены на рисунке 9. 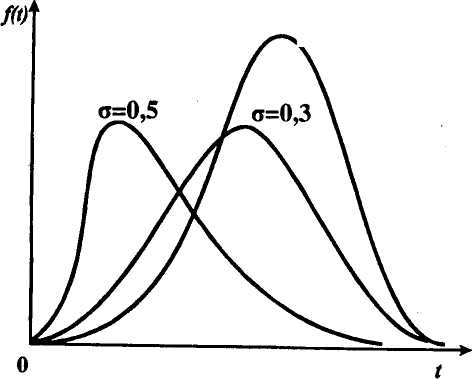 Рисунок 9 Плотность логарифмически нормального распределения для различных σ 13 Гамма-распределение Гамма-распределение является двухпараметрическим распределением, оно занимает важное место в математической статистике и теории надежности. Это распределение имеет ограничение с одной стороны (0 Если параметр формы кривой распределения α - целое число, то гамма-распределение описывает время, необходимое для появления α событий (отказов), при условии, что они независимы и появляются с постоянной интенсивностью λ. В большинстве случаев это распределение описывает наработку системы с резервированием, отказов стареющих элементов, время восстановления системы и т.д. При различных количественных значениях параметров гамма-распределение принимает самые разнообразные формы, что и объясняет его широкое применение. Плотность вероятности гамма-распределения определяется равенством, если λ > 0 и α > 0: 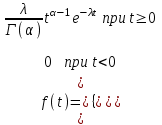 , (106) , (106)где Г(α)= 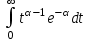 Функция распределения: 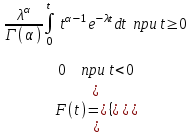 , (107) , (107)Функция надежности выражается формулой:  , (108) , (108)Математическое ожидание и дисперсия соответственно равны: 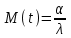 ; ; 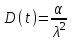 (109) (109)При α < 1 интенсивность отказов монотонно убывает, что соответствует периоду приработки изделия. При а > 1 интенсивность отказов возрастает, что характеризует период изнашивания и старения элементов. При α = 1 гамма-распределение совпадает с экспоненциальным распределением; при α > 10 гамма-распределение приближается к нормальному закону. Если α принимает значения произвольных целых положительных чисел, то такое гамма-распределение называют распределением Эрланга. Если значение α кратно 1/2 и λ = 1/2, то гамма-распределение совпадает с распределением хи-квадрат (χ2). Кривые плотности распределения приведены на рисунке 10. 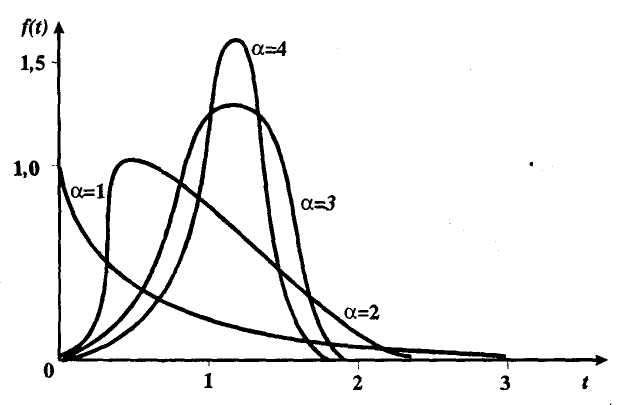 Рисунок 10 Кривые плотности гамма-распределения Если случайные величины Т1 и Т2, ..., Тn независимы и имеют нормальное распределение, причем математическое ожидание и дисперсия этих величин соответственно равны: 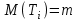 ; ; 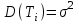 , (110) , (110)Функция распределения величины:  , (111) , (111)носит название распределения χ2 (хи-квадрат). Плотность распределения χ2 имеет вид: 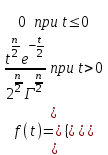 , (112) , (112)где n - число степеней свободы. Математическое ожидание и дисперсия соответственно равны: 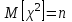 ; ; 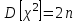 , (113) , (113)14 Распределение хи-квадрат случайной величины Распределение χ2 нашло применение при проверке статистических гипотез о виде распределения случайной величины Т, а также в теории надежности - при определении доверительных границ. Распределение хи-квадрат может быть определено как сумма квадратов n-независимых случайных величин с нулевым средним значением и единичным средним квадратическим отклонением. На рисунке 11 показаны формы кривых распределения. Следует отметить, что при n = 1 кривая несимметрична, а при n = 6 уже приближается к симметричной. При n > 30 кривая χ2 приближается к кривой нормального распределения.  Рисунок 11 Форма кривых χ2 распределения для n = 1 и n = 6 15 Бета-рапределение случайной величины В задачах математической статистики и теории надежности важное значение имеет бета-распределение, плотность вероятности которого задается формулой 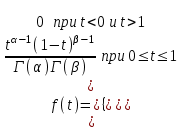 , (114) , (114)Математическое ожидание равно: 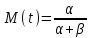 , (115) , (115)Дисперсия выражается формулой: 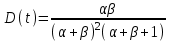 , (116) , (116)Графически плотность распределения изображена на рисунке 12. 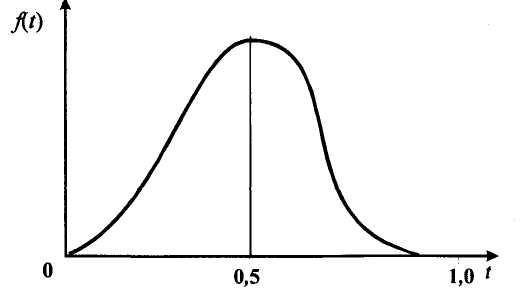 Рисунок 12 Плотность бета-распределения Если случайные величины ξ и η независимы, при этом величина ξ, распределена нормально с математическим ожиданием, равным нулю М[ξ]=0 и дисперсией, равной единице D[ξ] = 1, а величина η2 имеет распределение χ2 , то отношение ξ/η распределено по закону Стьюдента (Госсета) с плотностью вероятности вида:  , (117) , (117)Математическое ожидание и дисперсия соответственно равны: 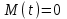 ; ;  , (118) , (118)16 Закон равномерного распределения случайной величины При решении практических задач часто встречаются случайные величины, о которых известно, что их возможные значения лежат в некотором интервале, причем все значения случайной величины одинаково вероятны, т.е. обладают одной и той же вероятностью. В качестве примера рассмотрим вертикально поставленное на оси симметричное колесо (рисунок 13), которое разгоняется и затем вследствие трения останавливается. Рассматривается случайная величина: φ - угол, который после остановки будет составлять с горизонтом фиксированный радиус колеса ОА. Очевидно, величина φ распределена с равномерной плотностью на участке (0, 2π). Рассмотрим случайную величину Т, подчиненную закону равномерного распределения на участке от α до β (рисунок 14), и напишем для нее выражение плотности f(t). Плотность распределения f(t) постоянна и равна с на отрезке (α, β); вне этого отрезка равна нулю: |
