вопросы. вопросы надежности. 1 Анализ задач исследования надежности

• Название: 1 Анализ задач исследования надежности
• Анкор: вопросы
• Дата: 23.06.2020
• Размер: 0.65 Mb.
• Имя файла: вопросы надежности.docx
• Тип: Документы; #132174
• страница: 3 из 6

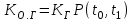, (42)
где P(t₀,t₁) - вероятность безотказной работы объекта в интервале (t₀,t₁)

t₀- момент времени, с которого возникает необходимость приме­нения объекта по назначению;

t₁ - момент времени, когда применение объекта по назначению прекращается.

Коэффициент К_Г в формуле (25) определяют для периода ожида­ния работы, непосредственно предшествующего моменту t_O, когда возни­кает необходимость в применении объекта.
29 Основные показатели невосстанавливаемого и восстанавливаемого элемента

К основным характеристикам (показателям) надежности невосста-навливаемого элемента относятся: наработка до отказа, интенсивность отказов, вероятность безотказной работы, вероятность отказа, средняя наработка на отказ, средний ресурс, гамма-процентный ресурс, назначен­ный ресурс, установленный ресурс, средний срок службы, установлен­ный срок службы, средний срок сохраняемости, гамма-процентный срок сохраняемости, назначенный срок хранения, установленный срок сохра­няемости.

К характеристикам (показателям) надежности восстанавливаемого элемента относятся все показатели надежности невосстанавливаемого элемента и дополнительно средняя наработка между отказами, параметр потока отказов, среднее время восстановления, вероятность восстановле­ния, коэффициент готовности, коэффициент технического использова­ния, коэффициент оперативной готовности.

30 Характеристики долговечности: ресурс и срок службы.

Средний ресурс - математическое ожидание ресурса. Статистическая оценка среднего ресурса:

, (43)
где T_pi - ресурс i-го объекта;

N- число объектов, поставленных на испы­тания или в эксплуатацию.

Гамма-процентный ресурс представляет собой наработку, в течение которой объект не достигает предельного состояния с заданной вероят­ностью γ, выраженной в процентах.

Значение гамма-процентного ресурса определяют с помощью кри­вых распределения ресурсов (рисунок 3).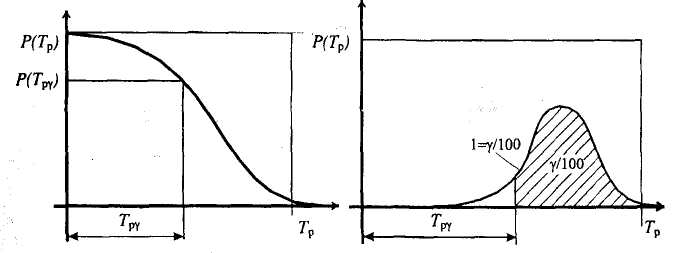

Рисунок 3 Определение значения гамма-процентного ресурса:

а и б- кривые соответственно убыли и распределения ресурсов
Вероятность обеспечения ресурса Т_Р.γ соответствующую значению γ/100, определяют по формуле:
, (44)

где Т_Р.γ - наработка до предельного состояния (ресурса).

Гамма-процентный ресурс является основным расчетным показате­лем для подшипников и ряда других элементов. Существенное достоин­ство этого показателя - возможность его определения до завершения ис­пытаний всех образцов. В большинстве случаев для различных элементов используют 90 % ресурс. Если отказ влияет на безопасность, то гамма-ресурс приближается к 100 %.

Назначенный ресурс - суммарная наработка, при достижении кото­рой применение объекта по назначению должно быть прекращено неза­висимо от его технического состояния.

Под установленным ресурсом понимается технически обоснованная или заданная величина ресурса, обеспечиваемая конструкцией, техноло­гией и эксплуатацией, в пределах которой объект не должен достичь пре­дельного состояния.

Средний срок службы - математическое ожидание срока службы. Статистическую оценку среднего срока службы определяют по формуле:
, (45)
где Т_{сл i} - срок службы i-го объекта.

Гамма-процентный срок службы представляет собой календарную продолжительность эксплуатации, в течение которой объект не достигает предельного состояния с вероятностью γ, выраженной в процентах. Для его расчета используют соотношение:
, (46)
Назначенный срок службы - суммарная календарная продолжитель­ность эксплуатации, при достижении которой применение объекта по назначению должно быть прекращено независимо от его технического состояния.

Под установленным сроком службы понимают технико-экономически обоснованный или заданный срок службы, обеспечиваемый конст­рукцией, технологией изготовления и эксплуатацией, в пределах которо­го объект не должен достичь предельного состояния.
1 Показатели сохраняемости

Средний срок сохраняемости - математическое ожидание срока со­храняемости объекта. В статистической трактовке этот показатель опре­деляют по формуле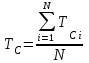

, (47)
где Т_Сi- срок сохраняемости i-го объекта.

Гамма-процентный срок сохраняемости - календарная продолжи­тельность хранения и (или) транспортировки объекта, в течение и после которой показатели безотказности, долговечности и ремонтопригодности объекта не выйдут за установленные пределы с вероятностью у, выра­женной в процентах.

Как и гамма-процентный ресурс, значение гамма-процентного срока сохраняемости определяют, используя выражение:
, (48)
Назначенный срок хранения - календарная продолжительность хране­ния в заданных условиях, по истечении которой применение объекта по назначению не допускается независимо от его технического состояния.

Под установленным сроком сохраняемости понимают технико-экономически обоснованный (или заданный) срок хранения, обеспечи­ваемый конструкцией и эксплуатацией, в пределах которого показатели безотказности, долговечности и ремонтопригодности объекта сохраняют­ся теми же, какими они были у объекта до начала его хранения и (или) транспортировки.

1. 
   Элементы теории вероятностей и математической статистики,
   

применяемые в теории вероятностей.

2. 
   Относительная частота и вероятность появления события. Теоремы
   

сложения и умножения вероятностей.
2 Случайное событие.
Теория вероятностей изучает случайные события, которые не предусмотрены нормальным протеканием технологического процесса на исправной машине. К таким событиям относятся, например, обрывы ремней, поломки деталей и др.

Все события делятся на:

- достоверные, которые обязательно произойдут при определенных условиях;

- невозможные, о которых заранее известно, что они не произойдут при определенных условиях;

- случайные о которых заранее не известно, произойдут они или нет.

Если события многократно повторяются при одних и тех же условиях, то они являются статически определимыми, или однородными. Основным требованием теории вероятностей к изучаемым событиям является постоянство их отношения к общему количеству всех наблюдений.
3 Вероятность появления случайного события

Рассматривая случаи появления или отсутствия события А в боль­шом числе испытаний, можно установить определенные закономерности появления этого события. Если при проведении n₁ испытаний событие А имело место m₁ раз, то относительную частоту появления события А определяют из соотношения:
, (49)
Если событие А имело место в каждом из n₁ испытаний, т.е. n₁= m₁ то . Если событие А не наступило ни в одном из n₁ испытаний,

т.е. m₁=0, 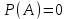. При проведении серии последовательных испы­таний получим соотношения: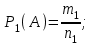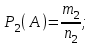
, (50)
Относительная частота становится все более устойчивой при увели­чении числа испытаний. Такая закономерность была замечена давно и подтверждена результатами решения многочисленных примеров. Самы­ми известными примерами являются примеры бросания монеты или иг­ральной кости. Так, при большом числе бросаний монеты относительная чистота выпадания герба равна 1/2 и равна относительной частоте выпа­дания цифры. При большом числе бросаний игральной кости относи­тельная частота выпадания каждой стороны, на которой изображены цифры от 1 до 6, равна 1/6.

Приведенные примеры показывают, что существует постоянная ве­личина (в нашем случае 1/2 или 1/6), около которой колеблется относи­тельная частота свершения случайного события и к которой она все более приближается с увеличением числа испытаний. Постоянную величину, к которой приближается относительная частота случайного события, назы­вают вероятностью случайного события А и обозначают символом Р(А). На практике при большом числе испытаний вероятность случайного со­бытия приближенно принимают равной относительной частоте этого со­бытия .

Математическим основанием этого утверждения является закон больших чисел (Я. Бернулли) - вероятность отклонения относительной частоты некоторого события А от вероятности Р(А) этого события более чем на произвольно заданную величину ε > 0 становится сколько угодно малой, если число испытаний n неограниченно возрастает.

Таким образом, вероятность события Р(А) представляет собой чис­ло, заключенное в интервале от нуля до единицы, т.е. справедливо нера­венство: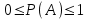
, (51)
4 Совместные и несовместные события. Теория сложение вероятностей

События могут быть совместными и несовместными. Два события называют несовместными, если в результате опыта они не могут поя­виться одновременно. И наоборот, события считаются совместными, если они появляются одновременно в результате такого опыта.

Вероятность суммы двух несовместных событий равна сумме веро­ятностей этих событий: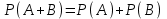
, (52)
Метод полной индукции позволяет использовать теорему сложения для произвольного числа несовместных событий. Так, вероятность сум­мы нескольких событий равна сумме вероятностей этих событий:
, (53)
Более удобная запись теоремы сложения:
, (54)

Следствие 1 Если события А₁ и А₂, ..., А_n образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
, (55)
Противоположными событиями называют два несовместных собы­тия, образующих полную группу.

Следствие 2 Сумма вероятностей противоположных событий рав­на единице:
, (56)
где 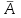- событие, противоположное событию А.

Вероятность суммы двух совместных событий А и В выражается формулой:
, (57)
Аналогично вероятность суммы трех совместных событий опреде­ляется выражением:
, (58)
Вероятность суммы любого числа совместных событий определяет­ся выражением

, (59)
Формула (59) выражает вероятность суммы любого числа событий через вероятности произведений этих событий, взятых по одному, по два, по три и т.д.

Аналогичную формулу можно написать для произведения двух со­бытий: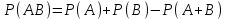
, (60)
для произведения трех событий: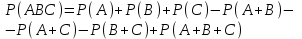
, (61)
Общая формула, выражающая вероятность произведения произ­вольного числа событий через вероятности сумм этих событий, взятых по одному, по два, по три и т.д., имеет вид :
, (62)
Формулы (59) и (62) находят практическое применение при пре­образовании различных выражений, содержащих вероятности сумм и произведений событий. В зависимости от специфики задачи в некоторых случаях удобнее бывает использовать только суммы, а в других только произведения событий.
5 Независимые и зависимые события. Теория умножения вероятностей

События могут быть независимыми и зависимыми. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называют зависимым от события В, если вероятность со­бытия А меняется в зависимости от того, произошло событие В или нет.

Понятие зависимости и независимости событий можно наглядно по­казать на следующих примерах.

Предположим, что опыт состоит в бросании двух мо­нет, при этом рассматривают следующие события: событие А - появле­ние герба на первой монете и событие В - появление герба на второй мо­нете.

В этом случае вероятность события А не зависит от того, произошло событие В или нет, следовательно, событие А независимо от события В.

Пусть в урне имеется два белых и один черный шар. Два человека вынимают из урны по одному шару, при этом рассматри­ваются следующие события: событие А - появление белого шара у перво­го человека и событие В - появление белого шара у второго человека.

Вероятность события А до того как станет известно что-либо о со­бытии В, равна 2/3. Если стало известно, что событие В произошло, то вероятность события А становится раной 1/2, из чего заключаем, что со­бытие А зависит от события В. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обо­значается Р(А/В).

Для условий примера

Теорема умножения вероятностей формулируется следующим обра­зом.

Вероятность произведения двух событий равна произведению ве­роятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место, т.е.:
, (63)
Очевидно, что при применении теоремы умножения безразлично, какое из событий - А или В - считать первым, какое вторым, и теорему можно записать так: два события называют независимыми, если появле­ние одного из них не изменяет вероятности появления другого.

Понятие независимых событий может быть распространено на слу­чай произвольного числа событий. Несколько событий называют незави­симыми, если любое из них не зависит от любой совокупности осталь­ных.

Вероятность произведения двух независимых событий равна произ­ведению вероятностей этих событий. Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий. В общем виде она формулируется так.

Вероятность произведения нескольких событий равна произведе­нию вероятностей этих событий, причем вероятность каждого следующе­го по порядку события вычисляют при условии, что все предыдущие имели место:
, (64)
В случае независимых событий теорема упрощается и принимает вид: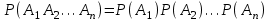
, (65)
т.е. вероятность произведения независимых событий равна произведению вероятностей этих событий.

Применяя знак произведения, теорему можно записать так: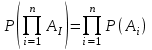
, (66)

6 Формула полной вероятности
Следствием обеих основных теорем - теоремы сложения вероятно­стей и теоремы умножения вероятностей - является формула полной ве­роятности.

Пусть требуется определить вероятность некоторого события А, ко­торое может произойти вместе с одним из событий: Н₁, Н₂, ….Н_n обра­зующих полную группу несовместных событий, называемых гипотезами. В этом случае:
, (67)
т.е. вероятность события вычисляется как сумма произведений вероятно­сти каждой гипотезы на вероятность события при этой гипотезе.
7 Формула Бернулли.

В практике применения теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются многократно. В результате каждого опыта может появиться некоторое событие А, причем представляет интерес не резуль­тат каждого отдельного опыта, а общее число появлений события А в результате серии опытов.

Если проводят n независимых опытов, в каждом из которых событие появляется с вероятностью р, то вероятность того, что событие появится ровно m раз, выражается формулой Бернулли:
, (68)
где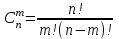


8 Вероятностные законы распределения

Вероятностные законы распределения могут быть представлены в виде функций (рисунок 5):

распределения
, (69)
плотности распределения
, (70)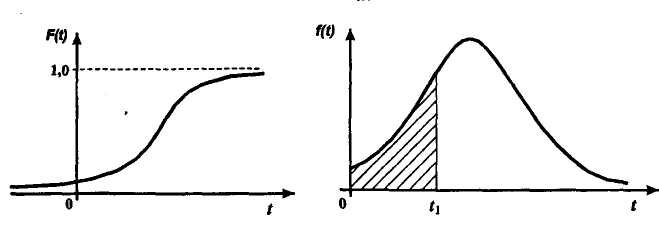


а) б)

Рисунок 5 Кривые:

а - функции распределения; б - плотности распределения
Заштрихованная площадь под кривой плотности распределения на участке (0; t₁) представляет собой вероятность попадания случайной ве­личины на этот участок. Если на оси абсцисс отложить наработку, то площадь под кривой, лежащая слева от точки t₁, определяет вероятность F(t₁) появления отказов в интервале (0; t₁), а площадь, лежащая справа от t₁, определяет вероятность P(t₁) отсутствия отказов в том же интервале. Существуют различные функции распределения (плотности распределе­ния), зависящие от одного или нескольких параметров, и соответственно называются однопараметрическими, двухпараметрическими и многопа­раметрическими. В теории и практике надежности технических систем наибольшее применение нашли одно- и двухпараметрические законы распределения.
9 Экспоненциальный закон распределения

В природе, и особенно в технике широкое применение нашел закон экспоненциального распределения. Этот закон описывает надежность ра­боты изделия в период его нормальной эксплуатации (технического ре­сурса), когда постепенные (износовые) отказы еще не проявляются и на­дежность характеризуется внезапными отказами. Эти отказы вызывают­ся неблагоприятным сочетанием различных факторов и поэтому имеют постоянную интенсивность отказов λ. Приведем примеры неблагоприят­ного сочетания условий работы деталей машин, вызывающих их внезап­ный отказ. Для зубчатой передачи это может быть действием максималь­ной нагрузки на наиболее слабый зуб при его зацеплении; для элементов радиоэлектронной аппаратуры - превышение допустимого тока или тем­пературного режима. Экспоненциальное распределение часто называют основным законом надежности. Существенное достоинство этого закона состоит в том, что он имеет один параметр.

Экспоненциальным законом распределения часто описывается вре­мя безотказной работы различных изделий: сложных технических сис­тем, эксплуатируемых в период после приработки и до проявления по­степенных отказов; элементов радиоэлектронной аппаратуры; систем управления и т.д. Кроме того, этот закон используют при решении про­блем, связанных с обслуживанием сложных систем, в частности при описании закона восстановления. Экспоненциальное распределение приме­няют также для описания времени безотказной работы системы с боль­шим числом последовательно соединенных элементов, если каждый из элементов в отдельности не оказывает влияния на отказы других элемен­тов системы.

Экспоненциальное распределение является частным случаем расп- ределения Вейбулла и гамма-распределения.

Вероятность безотказной работы (функция надежности) определяет­ся выражением