лек. 1-д_ріс. «Жа_артыл_ан мазм_нда_ы «Математика» п_нін о_ыту _дісте. 1дріс. Жаартылан мазмндаы Математика пнін оыту дістемесі бастауыш мектептегі математика дістемесіні негіздері жайлы ылым
 Скачать 383.54 Kb. Скачать 383.54 Kb.
|
|
Қос теңсіздік бір жолға жазылған екі теңсіздіктен тұрады. Оны бұл теңсіздіктің шешімдер жиынын сан сәулесінен көруге болады. а) 3 < х <6. Оның шешімін барлық шешімдердің жиыны түрінде жазуға болады: {4, 5}. ә) 5 < x < 15. Олардың шешімін барлық шешімдердің жиыны түрінде жазуға болады: {6, 7, 8, 9, 10, 11, 12, 13, 14}. Осы дәріске ағымдық, аралық, қорытынды бақылау бойынша тест тапсырмалары және сұрақтар 1. «Алгебра элементтері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: санды теңдік және санды теңсіздік; санды өрнек, өрнектің мәні, өрнектердегі амалдарды орындаудың рет тәртібі, әрпі бар өрнек, өрнектерді қарапайым теңбе-тең түрлендірулер, теңдеулер және оларды шешу тәсілдері. 2. «Алгебра элементтері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: есепті алгебралық тәсілмен шешу. № 10 дәріс. «Геометрия элементтері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы Қарастырылатын сұрақтар (дәріс жоспары): 1. Бастауыш сыныптарда қарастырылатын геометрия элементтері, нысандары. 2. Геометриялық фигуралармен таныстыру, қарапайым салулар, геометриялық мазмұнды есептер. 3.Геометрия элементтерін кезеңдер бойынша оқыту технологиясы. Қарастырылатын сұрақтар (дәріс жоспары): Дәрістің қысқаша мазмұны: Бастауыш математика курсында қарастырылатын геометриялық ұғымдар курстың негізгі мәселесі теріс емес бүтін сандар нумерациясы мен оларға арифметикалық амалдар қолдану мәселелерінің мән-мағынасын ашумен қатар, орта буын «Геометриясының» жүйелі курсын оқытуға дайындық және оқушылардың ойлау қабілеттерін дамыту, математикалық білім сапасын арттыру мақсатында оқытылып-үйретіледі. Геометриялық материалдар оқушыларға геометриялық фигуралар, олардың қасиеттері, геометриялық шамалар туралы жалпы түсінік қалыптастыру, салу есептерін орындау, геометриялық мазмұнды есептерді шешу түрінде оқытылады. Геометриялық фигуралар математиканың алғашқы сабақтарында-ақ санау материалы ретінде қарастырылып, осы кезеңнің өзінде кейбір қасиеттері (үшбұрыштың қабырғалары – кесінділер, оның үш төбесі бар, үш бұрышы бар т.б.) оқытылып-үйретіледі. Бастауыш сыныптарда жазық (дөңгелек, үшбұрыш, шаршы, сопақша, тік төртбұрыш, шеңбер, бұрыш, кесінді, түзу, сәуле, нүкте, параллель түзулер) және кеңістіктік (текше, цилиндр, пирамида, конус, тік бұрышты параллелепипед) қарастырылады, оларды өлшемдері мен элементтерімен таныстырылады. Геометриялық фигуралардың көпшілігі остенсивті (көрсету арқылы) түрінде таныстырылғанымен, кейбір фигуралардың нақты анықтамалары (тік, сүйір, доғал бұрыштар, тік төтрбұрыш, шаршы) да сұралады. Бұған қоса, геометриялық шамалар – аудан, периметр және көлем – да оқытылып үйретіледі. Көпбұрыштардың элементтерімен оқушылар көпбұрыштардың төбелері нүктелер екендігімен танысады. Мысалы, мұғалім балаларға тақтада көрсетілгендей 3 нүктені белгілеп алады (нүктелер бір түзудің бойында жатқан жоқ), оларды кесінділермен қосуды және қандай фигура шыққандығын айтудан кейін оның қанша төбесі бар екендігін санап білуді оқиды. Бірінші сынып оқушыларының түзу және қисық сызық туралы түсінігі олардың әр түрлі практикалық жаттығуларды орындау үдерісінде қалыптасады. Мұнда түзу сызықты қисық сызықпен салыстырады. Мысалы, жіпті (бау, шпагат) кереді, содан кейін оны ол салбырап тұратындай етіп, босатады. Түзу жол мен жалғыз аяқ қисық жол кескінделген суреттерді қарастырады, парақ қағазды бүктеп, оны қайта жазып, иілген жері бойынша оны қияды т.с.с. Әр жағдайда қандай сызық (тура сызық па әлде қисық сызық па) пайда болғанын түсіндіріп отырады. Кесінді туралы ұғымды пысықтауға мынандай жаттығулар көмектеседі: айналадағы нәрселерден түзудің кесіндісін көрсету; екі нүктені кесіндімен қосу; бір түзудің бойында жатқан үш нүкте арқылы кесінді жүргізу; осыдан пайда болған барлық кесінділерді көрсету. Кесінділерді өлшегенге дейін тең және тең емес кесінділер туралы ұғым енгізіледі. Осы қатынастарды тағайындау тәсілі (беттестіру арқылы) түсіндіріледі. Алдағы уақытта сантиметрмен, дециметрмен танысқаннан кейін оқушылар кесінділерді өлшеуде және сызуда көптеген жаттығуларды орындайды. Шеңбер мен дөңгелектің ұсқастықтары мен айырмашылықтары айтылады: ұқсастықтары: элементтері бірдей, яғни екеуінің де центрі, радиусы және диаметрі бар; айырмашылықтары: дөңгелектің ауданы, ал шеңбердің ұзындығы болады. Текше мен тік бұрышты параллелепипед жайлы да материалдар салыстыру арқылы жүзеге асырылады. Бұлардың ұқсастықтары өлшемдері мен элементтері бірдей, яғни өлшемдері: екеуінің де ұзындықтары, биіктіктері, ендері болады. Элементтері: 6 жағы, 8 қыры, 12 төбесі болады. Айырмашылықтары: текшенің барлық жақтары - шаршылар, ал тік бұрышты параллелепипедтің жақтары - тік төртбұрыштар. Геометриялық материалдарға жататын мәселелердің бір тобы – геометриялық салулар. Геометриялық салулар фигураны ерікті өлшеммен салу және берілген параметрлер бойынша салу деп бөлінеді. Салу есептерін орындауда оқушылар геометриялық фигуралардың қасиеттеріне көз жеткізеді, бастауыш математика курсы қарастырмайтын кейбір геометрияның жүйелі курсының мәселелерін де ұғынады. Жалпы салу есептері мынадай 4 кезеңнен тұрады: есепті талдау, салу, дәлелдеу, зерттеу. Бастауыш мектепте оқушылар еркін өлшеммен кез-келген фигураны, ал белгілі бір параметрлер бойынша тек кесінді, тік төртбұрыш пен шаршыны ғана салады. Циркульдің көмегімен дөңгелек және шеңбер салу, бұрыштар мен үшбұрыштардың бұрыштарын транспортирдің көмегімен өлшеу, үшбұрыштың барлық қабырғаларының қосындысы 1800 -қа тең болатынын үйренеді. ● Сызығы бар қағазда оның төбелерін білдіретін нүктелерді қоса отырып, тік төртбұрыш пен шаршыны сызғыштың көмегімен салуға болады.  ● Сызығы жоқ қағазда суреттегідей бұрыштықтың көмегімен алгоритм бойынша тік төртбұрыш салуға болады. Бұрыштықтың көмегімен қабырғалары 4 см және 2 см болатын тік төртбұрышты алгоритм бойынша сал: * Дәптердің торкөздерімен сәйкес келмейтіндей, ұзындығы 4 см кесінді сыз. * Кесіндінің екі ұшынан бұрыштықтың көмегімен екі тік бұрыш сыз. * Кесіндінің ұшынан бастап, өлшей отырып әр сәуленің бойынан 2 см өлшеп ал да нүкте қой. * Белгіленген екі нүктені кесіндімен қос. * Шыққан фигураның берілген қабырғалары бойынша тік төртбұрыш екендігіне көзіңді жеткіз. Геометриялық мазмұнды есептер бірінші сыныптан бастап оқытыла бастайды. геометриялық мазмұнды есептерге кесінділердің ұзындықтарын табу, ауданды, периметрді табумен, көлемді табумен, тік бұрышты параллелепипедтің жақтарының аудандарын табумен байланысты есептер жатады. Осы дәріске ағымдық, аралық, қорытынды бақылау бойынша тест тапсырмалары және сұрақтар 1. «Геометрия элементтері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: қарапайым геометриялық фигуралар, олардың қасиеттері мен белгіленуі; қарапайым геометриялық салулар; геометриялық мазмұнды есептер. 2.«Геометрия элементтері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: геометриялық шамалар (фигураның периметрі, ауданы мен көлемі) және көпбұрыштардың периметрлерін, тік төртбұрыштың (шаршының) ауданын, тік бұрышты параллелепипедтің (текшенің) көлемін есептеп табу. Начало формы 11-дәріс. «Математикалық модельдеу (жай есептер және оларды шешу)» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы Қарастырылатын сұрақтар (дәріс жоспары): 1. Есеп, оның түрлері, шығару тәсілдерін талдау. 2. Жай есептердің түрлері, шығару, модельдеудің үлгілеріне талдаулар жасау. 3. Жай есептерді есептерді шығаруға үйрету технологиясы. Дәрістің қысқаша мазмұны: «Есеп» ұғымымен айқын түрде таныстыру бұрынғы оқулықтарда да бар және әдістемелері ұқсас. Ол үшін көрнекілік ретінде асықтар мен қоржын алып келіп, нақты практикалық іс-әрекет түрінде көрсету қажет. Мысалы. «Асанда 3 асық бар еді. Оған атасы тағы 1 асық берді. Асанда неше асық болды?» есебі берілсін. Асанда 3 асық бар еді. (Асықтар көрсетіліп, қоржынға салынады). Оған атасы тағы 1 асық берді. (олар да көрсетіледі де, қоржынға салынады). Асанда неше асық болды? «Балалар, бұл – есеп» - деп хабарланады. «Есеп» деген жазуы бар карточка тақтаға ілінеді. Қоржыннан асықтар шығарылады да, есептің шарты қайтадан айтылады. - Асанда 3 асық бар еді. Оған атасы тағы 1 асық берді. - Бұл – есептің шарты. («Шарты» деген карточка тақтаға ілінеді) - Асанда неше асық бар? Бұл – есептің сұрағы. («Сұрағы» деген карточка да тақтаға ілініп, алдыңғы үш термин арасына стрелкалар қойылады: Есепті шешу үшін заттық иллюстрация көрсетіледі. Ары қарай есептің шешу жолын іздестіру жұмысы жүргізіледі. - Асанда неше асық бар еді? (3) - Тағы атасы неше асық береді? (1) - Балалар, асықтар артты ма, кеміді ме? - Артты. Онда қандай амал қолданамыз? 3 + 1 = 4. Бұл – есептің шешуі - Сонда қанша болды (4) - Асанда неше асық болды? - 4 асық, бұл – есептің жауабы. Әрбір жаңадан енгізілген термин тақтаға ілініп отырады. Сонда тақтада тізбек шығады, осы тізбекті келесі сабақта да қолдануға болады. Оқушылар көре отырып, есептің әр бөлігін және есеппен байланысты терминдерді естерінде сақтауға негіз жасалады. Бірінші сынып оқушыларын есептің мәнді белгілерімен, яғни 1) есеп мәтінмен беріледі; 2) сол мәтінде өмірде кездесетін нақты жағдаят сипатталады; 3) есептің сұрағы болады; 4) сол сұраққа жауап беру үшін қандай да бір амал орындалады сияқты мәселелерімен таныстыру, оларды анықтай алу, есепті басқа тапсырмалардан ажырата алу жұмыстарын жүргізу жүзеге асырылады. Жай есеп дегеніміз бір амалмен шығарылатын, ал құрама дегеніміз екі немесе одан да артық амалмен шығарылатын есептер. Жай есептің бірнеше түрлері бар: І. Арифметикалық амалдардың мән-мағынасын ашуға арналған жай есептер. Бұлар өз кезегінде бірнеше жай есептерге бөлінеді: а) қосындыны табуға арналған жай есептер. ә) қалдықты табуға арналған жай есептер. Б) бірдей қосылғыштардың қосындысын табуға арналған жай есептер в) тиісінше бөлуге арналған жай есептер. Г) теңдей бөлуге арналған жай есептер. ІІ. Амал қатынастарының мән-мағынасын ашуға арналған жай есептер. А) бірнеше бірлікке артық санды табуға арналған жай есептер. ә) бірнеше бірлікке кем санды табуға арналған жай есептер. Б) айырмалық салыстыруға арналған жай есептер. В) бірнеше бірлікке есе артық сандытабуға арналған жай есептер. Г) бірнеше бірлікке есе кем сандытабуға арналған жай есептер. Д) еселік салыстыруға арналған жай есептер. Алдыңғы топ жай есептердің алғашқы екі түрі және 2 топ жай есептердің алдыңғы үш түрі 1-сыныпта, ал қалғандары 3-сыныпта қарастырылады. ІІІ. Амал компоненттері мен нәтижелері арасындағы байланысқа негізделген жай есептер: а) белгісіз қосылғыштарды табуға арналған жай есептер, ә) белгісіз азайғышты табуға арналған жай есептер. Б) белгісіз азайтқышты табуға арналған жай есептер. В) белгісіз көбейткіштерді табуға арналған жай есептер. Г) белгісіз бөлінгішті табуға арналған жай есептер. Ғ) белгісіз бөлгішті табуға арналған жай есептер. Алғашқы үш есеп 1-сыныпта, ал қалғандары 3-сыныпта қарастырылады. ІҮ. «Үлес және бөлшек» ұғымдарының мән-мағынасын ашуға арналған жай есептер: а) үлесі бойынша санды (бүтінді) табуға арналған жай есептер. ә) саны (бүтіні) бойынша үлесті табуға арналған жай есептер. Ү. Пропорцианал шамалар арасындағы тәуелділікті ашуға арналған жай есептер: шамалар «үштігі»: а) бағасы, саны, құны. ә) қашықтық, уақыт, жылдамдық. б) заттың массасы, жалпы саны, жалпы массасы. в) тік төртбұрыштың ауданы, ені, ұзындығы. Есепті шешу үдерісінің міндетті кезеңдері мыналар: · есеп мәтінін шапшаң және түсініп оқу. · есептің шешуін іздестіру немесе шешу жоспарын құру. · есептің шешуін жазу. · жауабын бөліп көрсету және тексеру. Есепті талдау үлгісі: 1. Есеп не жайында? 2. Есепте не белгілі? (бұнда есептің шарты талданады) 3. Есепте не білгісіз? Нені табуымыз қажет? (бұдан есептің сұрағы шығады) 4. Алдымен нені табуға болады? 5. Оны қандай амалмен табамыз? Неге? 6. Есеп неше амалмен шешілді? Осы дәріске ағымдық, аралық, қорытынды бақылау бойынша тест тапсырмалары және сұрақтар 1. «Есеп және оны шешу үдерісі» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: «есеп» ұғымы; кері есептер; 2. «Есеп және оны шешу үдерісі» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: жай (әр амалдың мән-мағынасын ашуға, айырмалық және еселік салыстыруға, шамалар арасындағы байланыстар мен тәуелділікке негізделген, «үлес» ұғымымен және пропорционал шамалармен байланысты) есептер; № 12 дәріс. «Математикалық модельдеу (құрама есептер және оларды шешу)» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы Қарастырылатын сұрақтар (дәріс жоспары): 1. Құрама есепті енгізу әдістемесі. 2.Бастауыш сыныптарда кездесетін құрама есептер. 3. Құрама есептердің түрлері шығаруға үйрету технологиясы. Дәрістің қысқаша мазмұны: Бастауыш сыныптарда құрама есептердің жай есептер сияқты нақты топтары қарастырылмағанымен, есептің сұрағына орай оның түрін ажыратуға болады. М: Дүкенге 70 кг-дық 6 қап картоп және 50 кг-дық 8 қап сәбіз әкелінді. Сәбізге қарағанда картоптан неше кг артық әкелінді? Бұл есептің сұрағына қарап, айырмалық салыстыруға берілген құрама есеп екенін анықтауға болады. Дегенмен, бастауыш сыныптарда қарастырылатын құрама есептің мынадай түрлері бар: Қозғалысқа берілген есептер; Пропорционал бөлуге берілген есептер; «Бірігіп жұмыс жасауға» арналған есептер; Екі айырма бойынша белгісізді табуға берілген есептер. Жоғарыда аталған құрама есептердің атауларын оқушылардың білуі шарт емес. Тек есеп шығаруда амалды дұрыс әрі саналы түрде таңдап алу талап етіледі. Есепті шешу үдерісі жай есепті де, құрама есепті шешуде де бірдей болғанымен, жай есептердің шешу жоспарын құруда қысқаша жазудан гөрі көрнекіліктің басқа да түрлерін қолдану қажет. Құрама есептерді шешудің екі түрлі тәсілі бар: алгебралық және арифметикалық. Есепті шешудің алгебралық тәсілі дегеніміз есепті теңдеу құру арқылы шешу, ал арифметикалық тәсілі дегеніміз есептерді арифметикалық амалдардың немесе өрнек құру арқылы шешуді айтамыз. Екінші сыныпта есептер алдымен арифметикалық тәсілмен шығарылады. Есепті шешу үшін өрнек құру кезінде алғашқы орындалатын амал өрнегі дәптердің ортасына қарай жазылады, кейінгі сандар мен амал таңбалары, яғни жазу не солға, не оңға қарай жалғасуы мүмкін. Төртінші сыныпта орта буын математикасын өтуге дайындық түрінде есептерді жеке-жеке амалдар, яғни арифметикалық тәсілмен шешу қарастырылады. Алгебралық тәсілмен шешу төртінші сыныпта оқылып-үйретіледі. Мұндай тәсілмен есептерді шешу кезінде алдымен жай есептерге теңдеу құру қарастырылады. Жай есептердің бір топ түрлерін, яғни арифметикалық амал атаулары мен нәтижелері арасындағы байланысқа арналған жай есептерді шешу кезінде оқытылып-үйретіледі. Белгісіз қосылғыштарды, белгісіз азайғыш пен азайтқышты табуға арналған есептерді шешу кезінде алгебралық тәсіл қолданылады. Мысалы: «Ағашта бірнеше торғай қонып отырған еді. Оларға тағы екі торғай келгенде, олар 13 болды. Бастапқыда неше торғай отырған еді?» Бұл-белгісіз қосылғышты табуға арналған жай есеп, белгісіз қосылғышты х-пен белгілейміз, сонда мынадай теңдеу шығады: х+2=13. Есепті шешу үдерісінің міндетті кезеңдері мыналар: · есеп мәтінін шапшаң және түсініп оқу. · есептің шешуін іздестіру немесе шешу жоспарын құру. · есептің шешуін жазу. · жауабын бөліп көрсету және тексеру. Есепті талдау үлгісі: 1. Есеп не жайында? 2. Есепте не белгілі? (бұнда есептің шарты талданады) 3. Есепте не білгісіз? Нені табуымыз қажет? (бұдан есептің сұрағы шығады) 4. Алдымен нені табуға болады? (жауап бермесе, жетекші сұрақтар қояямын). 5. Оны қандай амалмен табамыз? Неге? 6. Енді сұраққа жауап бердік пе? 7. Онда нені тауып алуға болады? (жауап бермесе, жетекші сұрақтар қояямын). 8. Есеп неше амалмен шешілді? Құрама есепті шығар: Мектептің информатика кабинетіндегі компьютерде 8 қыз бала және 9 ұл бала жұмыс жасап отыр еді. Олардың 12-сі жұмысын бітірді. Неше бала компьютерде әлі жұмыс жасап отыр? Есепті екі бөлікке бөл: шарты мен сұрағына. Есептің сұрағын оқы. Есептің сұрағына бірден жауап беруге бола ма, ойлан. Неліктен болмайды? Ол үшін нені білу керек? Қандай амал және оны қандай сандармен орындау керектігін айтып бер. Енді сұраққа жауап бере аламыз ба? Қандай амал және оны қандай сандармен орындау керектігін айтып бер. Есеп берілсін: Арасы 290 км болатын екі станциядан бір мезгілде бір-біріне қарама-қарсы екі пойыз шықты. Бірінші пойыз 2 сағатта 140 км жол жүрді. Екінші пойыздың жылдамдығы қандай? Осы дәріске ағымдық, аралық, қорытынды бақылау бойынша тест тапсырмалары және сұрақтар 1. «Есеп және оны шешу үдерісі» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: құрама есептер, геометриялық мазмұнды есептер; шығармашылық әрекетпен байланысты тапсырмалар, есепті арифметикалық, алгебралық, графикалық және практикалық тәсілмен шешу. «Есеп және оны шешу үдерісі» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы: есепті арифметикалық, алгебралық, графикалық және практикалық тәсілмен шешу. № 13 дәріс. «Математикалық модельдеу (есептерді модельдеу)» мазмұндық-әдістемелік желі материалдарын оқыту әдістемесі Қарастырылатын сұрақтар (дәріс жоспары): 1. Есеп шығаруда қолданылатын модель түрлері. 2. Есеп шығаруда қолданылатын көрнекіліктер. Дәрістің қысқаша мазмұны: Есепті графиктің, сызбаның, схеманың көмегімен иллюстрациялауға болады. «Жаңа буын оқулығы бойынша бастауыш сыныптарда математиканы оқыту әдістемесінде» есепті иллюстрациялаудың түрлеріне талдау жасалған: 1. График түрінде иллюстрациялау. Графиктер – бұл «кесінді» түріндегі иллюстрация, сондықтан шамалар ұзындық бірліктерімен немесе шамалар арасындағы қатынастар берілген есептерді графикпен иллюстрациялаған жеңіл. Мысалы: «Бір бумада 15 м мата болды. Алдымен 5 м, содан соң 4 м сатылды. Бумада неше метр мата қалды? 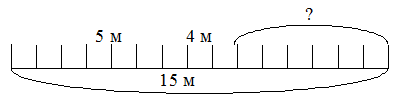 Графиктік модель жағдаяттарды нақты түсінуге, деректер мен ізделінді арасындағы байланыстың құрылымын анық көрсетуге ықпал етеді, яғни есептің шешу жолын жорамалдайды, әр түрлі тәсілмен есептің шешуін өрнек арқылы жазуға оқушыларды үйретеді. І. 15-5-4=6 (м) ІІ. 15-(5+4)=6 (м) Тағы бір мысал: «Бір мектептен жарысқа 18 бала, ал екінші мектептен 2 есе артық бала қатысты. Барлығы неше бала жарысқа қатысты?» 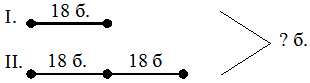 І. 18+18 · 2=54 (б) ІІ. 18 · 3=54 (б) Мұндағы есепті шығарудың екінші тәсілі графиктік және әлдеқайда тиімді болып табылады. 2.Сызба түрінде иллюстрациялау. Қозғалысқа берліген есепті сызба түрінде иллюстрациялау өте қолайлы, оның үстіне сызба қозғалмалы болуы мүмкін, оны өз кезегінде өзара кері есептерді құрастыру мен шығаруда қолдануға жақсы.  3.Схема түрінде иллюстрациялау. Схема – граф тәрізді сурет түріндегі модель. Мұндай сурет әлдеқайда қарапайым және есепті шығару барысында қажет болатын амалдың мәнін нақты бейнелейді, жағдаяттың сандық қатынасын, амал таңдауға мүмкіндік беретін деректер мен ізделінді арасындағы байланысты анық түрде көрсетеді. Мысалы, жоғарыда келтірілген есептердің схемасы мынадай: 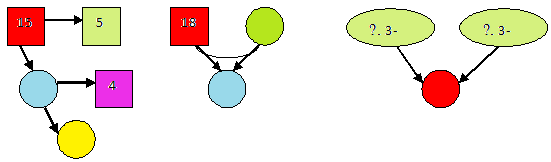 Сурет – Есептер схемасы Схеманың көмегімен модельдеудің осы тәсіліне үйрету 1-сыныпта жай есептерді шешуге үйрету кезеңінде басталады. Есеп мазмұны бойынша схема, график түрінде иллюстрациялау, есепті қысқаша жазу, заттық иллюстрация жасау оқушыға есептің сұрағына жауап беруіне көмектеседі. Тең бөліктерге бөлу. «Оқушылардың екі тобы әрқайсысы бірдей 8 жүйектің арам шөбін отады. Әр топ оқушылары қанша жүйектен отаған?» Е 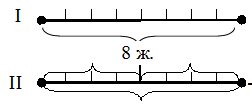 септе не белгілі? септе не белгілі?Оқушылар 8 жүйектің шөбін отады. Оқушылардың неше тобы отады? - 2 тобы 3.Санды бірнеше бірлікке кеміту. «Аққу 88 км, ал көгершін одан 26 км кем ұшты. Көгершін неше километр ұшты?» 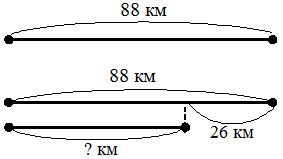 Алгоритмді пайдаланып, есепті дөңгелек диаграмма түрінде модельдеп көр: |
