Физика Теория. 1. Электромагнитная природа света. Сложение колебаний, понятие о когерентности. Интерференция световых волн. Расчет интерференционной картины от двух источников.
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
Дифракция Фраунгофера на системе щелей.
Дифракционной решеткой называется последовательность из большого числа N одинаковых параллельных щелей. Ширина каждой щели равна b, расстояние между соседними щелями, которое называется периодом решетки, равно d. Расположим параллельно решетке собирательную линзу, в фокальной плоскости которой поставим экран. Выясним характер дифракционной картины, получающейся на экране при падении на решетку световой волны (для простоты будем считать, что волна падает на решетку нормально). Каждая из щелей даст на экране картину. Картины от всех щелей придутся на одно и то же место экрана (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку Р от различных щелей, были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью лишь тем, что все интенсивности выросли бы в N раз. Однако, колебания от различных щелей являются в большей или меньшей степени когерентными; поэтому результирующая интенсивность будет отлична от 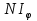 ( (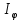 - интенсивность, создаваемая одной щелью). Предполагая, что радиус когерентности (максимальное поперечное направлению распространению волны расстояние, на котором возможно проявление интерференции) падающей волны намного превышает длину решетки. Так что колебания от всех щелей можно считать когерентными друг относительно друга. В этом случае результирующее колебание в точке Р представляет собой сумму N колебаний с одинаковыми амплитудами - интенсивность, создаваемая одной щелью). Предполагая, что радиус когерентности (максимальное поперечное направлению распространению волны расстояние, на котором возможно проявление интерференции) падающей волны намного превышает длину решетки. Так что колебания от всех щелей можно считать когерентными друг относительно друга. В этом случае результирующее колебание в точке Р представляет собой сумму N колебаний с одинаковыми амплитудами 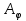 , сдвинутых друг относительно друга по фазе на одну и ту же величину δ . Интенсивность при этих условиях равна: , сдвинутых друг относительно друга по фазе на одну и ту же величину δ . Интенсивность при этих условиях равна: 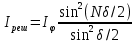 , где , где 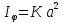 – интенсивность, создаваемая каждым из лучей в отдельности. Видно, что разность хода от соседних щелей равна – интенсивность, создаваемая каждым из лучей в отдельности. Видно, что разность хода от соседних щелей равна  Следов, разность фаз Следов, разность фаз 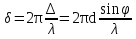
Дифракционный спектр – Распределение интенсивности на экране, получаемое вследствие дифракции (это явление приведено на нижнем рис.). Основная часть световой энергии сосредоточена в центральном максимуме. Сужение щели приводит к тому, что центральный максимум расплывается, а его яркость уменьшается (это, естественно, относится и к другим максимумам). Наоборот, чем щель шире ( b > λ ), тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При b >> λ в центре получается резкое изображение источника света, т.е. имеет мет прямолинейное распространение света. Эта картина будет иметь место только для монохроматического света. При освещении щели белым светом, центральный максимум будет иметь место белой полоски, он общий для всех длин волн (при 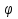 = 0 разность хода равна нулю для всех λ ). = 0 разность хода равна нулю для всех λ ).
Изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы (разделены для восприятия), если центральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого. При выполнении критерии Релея интенсивность «провала» между максимумами составляет 80% интенсивности в максимуме, что является достаточным для раз- решения линий 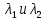 .Если критерий Релея нарушен, то наблюдается одна линия. .Если критерий Релея нарушен, то наблюдается одна линия.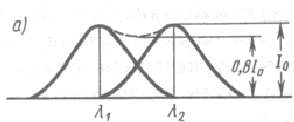
Дифракционная картина на решетке определяется как р-тат взаимной интерференции волн, идущих от всех щелей. Т.е. в дифракционной. решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся на одинаковых друг от друга расстояниях, то разность хода лучей, идущих от двух соседних щелей, будут для данного направления 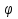 одинаковы в пределах всей дифракционной решетки: одинаковы в пределах всей дифракционной решетки: 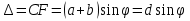 . Очевидно что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние минимумы интенсивности будут наблюдаться в направлениях, определяемых условием . Очевидно что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние минимумы интенсивности будут наблюдаться в направлениях, определяемых условием  . Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей . Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей 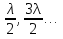 , посылаемых, например, от крайних левых точек М и С обеих щелей. Условие дополнительных минимумов: , посылаемых, например, от крайних левых точек М и С обеих щелей. Условие дополнительных минимумов: 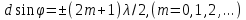 . Наоборот, действие одной щели будет усиливать действие другой, если . Наоборот, действие одной щели будет усиливать действие другой, если  т.е. условие максимумов. При двух щелях между двумя главными максимумами располагается один дополнительный минимум, а между каждыми главными максимумами при трех щелях располагается два дополнительных минимума, при четырех – три. Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие т.е. условие максимумов. При двух щелях между двумя главными максимумами располагается один дополнительный минимум, а между каждыми главными максимумами при трех щелях располагается два дополнительных минимума, при четырех – три. Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие  , а условие главных максимумов - , а условие главных максимумов - 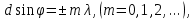 а условием дополнительных минимумов а условием дополнительных минимумов 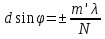 , где m' может принимать все целочисленные значения, кроме 0, N, 2N,…, т.е. тех, при которых dsinϕ = ±m'λ / N переходит в d sinϕ = ±mλ . Следовательно, в случае N щелей между двумя главными максимумами располагается N - 1дополнительных минимумов, разделенных вторичными максимумами. Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, след, более интенсивными и более острыми будут максимумы. Так как , где m' может принимать все целочисленные значения, кроме 0, N, 2N,…, т.е. тех, при которых dsinϕ = ±m'λ / N переходит в d sinϕ = ±mλ . Следовательно, в случае N щелей между двумя главными максимумами располагается N - 1дополнительных минимумов, разделенных вторичными максимумами. Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, след, более интенсивными и более острыми будут максимумы. Так как 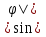 не может быть больше 1, то m ≤ d /λ , т.е. число главных максимумов определяется отношением периода решетки к длине волны. не может быть больше 1, то m ≤ d /λ , т.е. число главных максимумов определяется отношением периода решетки к длине волны.Разрешающая способность решетки. Разрешающей способностью спектрального прибора назовем безразмерную величину 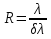 , где δλ -абсолютное значение минимальной разности длин волн двух соседних спектральных линий, при которой эти линии регистрируются раздельно. Пусть максимум m-го порядка для длины волны , где δλ -абсолютное значение минимальной разности длин волн двух соседних спектральных линий, при которой эти линии регистрируются раздельно. Пусть максимум m-го порядка для длины волны  наблюдается под углом наблюдается под углом 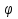 , т.е. , т.е. 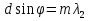 . При переходе от максимума к соседнему минимуму, разность хода меняется на λ / N , где N – число щелей решетки. Следовательно минимум . При переходе от максимума к соседнему минимуму, разность хода меняется на λ / N , где N – число щелей решетки. Следовательно минимум 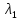 , наблюдаемый под углом , наблюдаемый под углом 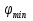 , удовлетворяет условию , удовлетворяет условию  . По критерию Релея (Изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами раз- решимы (разделены для восприятия), если цен- тральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифр. картины от другого), . По критерию Релея (Изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами раз- решимы (разделены для восприятия), если цен- тральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифр. картины от другого), 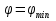 , т.е., m , т.е., m =m =m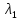 + +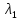 /N или /N или 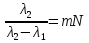 . Т.к. . Т.к. 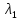 и и  близки ме- жду собой, т.е. близки ме- жду собой, т.е.  − −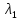 = δλ , то согласно R = λ /(δλ) : = δλ , то согласно R = λ /(δλ) : 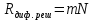 . Таким образом разрешающая способность дифракционной решетки пропорциональна порядку m спектров и числу N щелей, т.е. при заданном N увеличивается при переходе к спектрам высших порядков. . Таким образом разрешающая способность дифракционной решетки пропорциональна порядку m спектров и числу N щелей, т.е. при заданном N увеличивается при переходе к спектрам высших порядков.
Это не видимые глазом эл. магнитное излучение м длиной волны 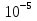 , ,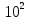 нм. Проникают через некоторые непрозрачные для видимого света материалы, испускаются при быстрых торможениях электронов в веществе и при квантовых переходах электронов с внешних эл. оболочек атома на внутренние. Поставим две дифракционные решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка (пусть ее штрихи вертикальны) даст в горизонтальном направлении ряд максимумов, положения которых определяются условием нм. Проникают через некоторые непрозрачные для видимого света материалы, испускаются при быстрых торможениях электронов в веществе и при квантовых переходах электронов с внешних эл. оболочек атома на внутренние. Поставим две дифракционные решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка (пусть ее штрихи вертикальны) даст в горизонтальном направлении ряд максимумов, положения которых определяются условием 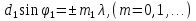 . Вторая решетка (с горизонтальными штрихами) разобьет каждый из образовавшихся таким образом пучков на расположенные по вертикали максимумы, положения которых определяются условием: . Вторая решетка (с горизонтальными штрихами) разобьет каждый из образовавшихся таким образом пучков на расположенные по вертикали максимумы, положения которых определяются условием: 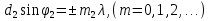 . В итоге дифракционная картина будет иметь вид правильно расположенных пятен, каждому из которых соответствуют два целочисленных индекса . В итоге дифракционная картина будет иметь вид правильно расположенных пятен, каждому из которых соответствуют два целочисленных индекса  и и 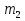 . Такая же дифракционная картина получается, если вместо двух реальных решеток взять одну прозрачную пластинку с нанесенными на нее двумя системами взаимно перпендикулярных штрихов. Дифракция так же наблюдается на трехмерных структурах. т.е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами являются все кристаллические тела. Однако их период слишком мал ( ≈ . Такая же дифракционная картина получается, если вместо двух реальных решеток взять одну прозрачную пластинку с нанесенными на нее двумя системами взаимно перпендикулярных штрихов. Дифракция так же наблюдается на трехмерных структурах. т.е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами являются все кристаллические тела. Однако их период слишком мал ( ≈ 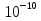 ,), чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов условие d > λ выполняется только для рентгеновских лучей. ,), чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов условие d > λ выполняется только для рентгеновских лучей.3. Естественный и поляризованный свет. Поляризация при отражении и преломлении на границе двух диэлектрических сред. Закон Брюстера. Закон Малюса. Естественная анизотропия. Поляризационные приборы. Сложение поляризованных колебаний. Четвертьволновые и полуволновые пластинки. Вращение плоскости поляризации. Искусственная анизотропия. Эффект Керра, эффект Фарадея.
Поляризованным светом называется свет, в котором направление колебаний светового вектора упорядочены каким-либо образом (световой вектор - 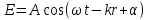 , где k – волновое число, r – расстояние, отсчитываемое вдоль направления распространения световой волны. Для плоской волны, распространяющейся в непоглощающей среде А = const, для сферической волны А убывает как 1/r). В естественном свете колебания различных направлений быстро и беспорядочно меняют друг друга. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление колебаний вектора Е, то имеем дело с частично поляризованным светом. Свет, в котором Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу, называется плоскополяризованным. Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называетсяся плоскостью поляризации. , где k – волновое число, r – расстояние, отсчитываемое вдоль направления распространения световой волны. Для плоской волны, распространяющейся в непоглощающей среде А = const, для сферической волны А убывает как 1/r). В естественном свете колебания различных направлений быстро и беспорядочно меняют друг друга. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление колебаний вектора Е, то имеем дело с частично поляризованным светом. Свет, в котором Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу, называется плоскополяризованным. Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называетсяся плоскостью поляризации.
Если угол падения на границу раздела двух диэлектриков (например, на поверхность стеклянной пластинки) отличен от нуля, отраженный и преломленные лучи оказываются частично поляризованными (при отражении от проводящей поверхности (например, от поверхности металла) получается эллиптический поляризованный свет). В отраженном луче преобладают колебания, перпендикулярные к плоскости падения (на рис. эти колебания обозначены точками), в преломленном луче – колебания, параллельные плоскости падения (на рисунке они изображены двусторонними стрелками). Степень поляризации зависимость от угла падения. Обозначим через 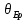 угол, удовлетворяющий условию угол, удовлетворяющий условию 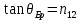 , где , где 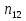 -показатель преломления второй среды преломления относительно первой. При угле падения -показатель преломления второй среды преломления относительно первой. При угле падения  равном равном 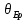 , отраженный луч полностью поляризован (он содержит только колебания, перпендикулярные к плоскости падения). Степень поляризации преломленного луча при угле падения, равном , отраженный луч полностью поляризован (он содержит только колебания, перпендикулярные к плоскости падения). Степень поляризации преломленного луча при угле падения, равном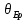 , достигает наибольшего значения, однако этот луч остается поляризованным только частично. , достигает наибольшего значения, однако этот луч остается поляризованным только частично.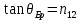 - закон Брюстера, а угол - закон Брюстера, а угол 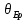 называют углом Брюстера. Легко убедиться в том, что при падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны. Степень поляризации отраженного и преломленного лучей при различных углах падения можно получить с помощью формул Френеля. Эти формулы вытекают из условий, налагаемых на электромагнитное поле на границе поле на границе двух диэлектриков. называют углом Брюстера. Легко убедиться в том, что при падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны. Степень поляризации отраженного и преломленного лучей при различных углах падения можно получить с помощью формул Френеля. Эти формулы вытекают из условий, налагаемых на электромагнитное поле на границе поле на границе двух диэлектриков.
 Пусть на поляризатор падает плоскополяризованный свет амплитуды 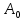 и интенсивности и интенсивности 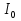 . Сквозь прибор пройдет составляющая колебаний с амплитудой . Сквозь прибор пройдет составляющая колебаний с амплитудой 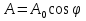 , где , где 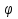 - угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением - угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением 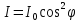 , где , где 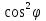 – доля интенсивности, которую несет с собой колебание, параллельное плоскости поляризатора. – доля интенсивности, которую несет с собой колебание, параллельное плоскости поляризатора.
Поляризатором называется устройство, поглощающее свет, поляризованный в одной плоскости, но пропускающее свет, поляризованный в перпендикулярной плоскости. Плоскость поляризации прошедшего света называют плоскостью пропускания поляризатора. Если линейно поляризованный свет интенсивностью I0 пропустить через поляризатор, плоскость пропускания которого составляет угол ϕ с плоскостью колебаний световой волны, то интенсивность прошедшей волны будет составлять 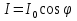 (закон Малюса). Объясняется это тем, что линейно поляризованный свет с амплитудой (закон Малюса). Объясняется это тем, что линейно поляризованный свет с амплитудой 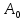 представляет собой сумму двух линейно поляризованных волн: волна, поляризованная в плоскости пропускания (ее амплитуда = представляет собой сумму двух линейно поляризованных волн: волна, поляризованная в плоскости пропускания (ее амплитуда = 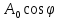 ), пройдет через поляризатор без изменений, а вторая волна будет поглощена. ), пройдет через поляризатор без изменений, а вторая волна будет поглощена.
Рассмотрим кристаллическую пластинку, вырезанную параллельно оптической оси. При падении на такую пластинку плоскополяризованного света, обыкновенный и необыкновенный лучи оказываются некогерентными (т.к. колебания каждого цуга разделяются между обыкновенным и необыкновенным лучами в одинаковой пропорции (зависящей от ориентации оптической оси пластинки относительно плоскости колебаний в падающем луче)). На входе в пласт-ку. Разность фаз δ этих лучей равна 0, на выходе из нее 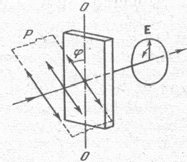 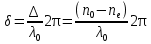 , где , где  , ,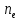 - показатели преломления обыкновенного и необыкновенного лучей (n=c/V). Вырезанная для параллельной оси пластинка, для которой - показатели преломления обыкновенного и необыкновенного лучей (n=c/V). Вырезанная для параллельной оси пластинка, для которой 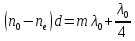 , (где m = 0,1,2,…), называется пластинкой в четверть волны. При прохождении через такую пластинку обыкновенный и необыкновенный лучи приобретают разность фаз, равную π /2 (разность фаз определяется с точностью до 2πm). Пластинка, для которой , (где m = 0,1,2,…), называется пластинкой в четверть волны. При прохождении через такую пластинку обыкновенный и необыкновенный лучи приобретают разность фаз, равную π /2 (разность фаз определяется с точностью до 2πm). Пластинка, для которой 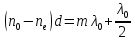 , называется пластинкой в полволны. Если через пластинку в полволны пропустить плоскополяризованный свет: пластинка в полволны поворачивает плоскость колебаний прошедшего через нее света на угол 2 , называется пластинкой в полволны. Если через пластинку в полволны пропустить плоскополяризованный свет: пластинка в полволны поворачивает плоскость колебаний прошедшего через нее света на угол 2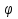 ( (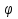 - угол между пл-тью колебаний в падающем луче и осью пластинки). Если пропустить плоскополяризованный свет через пластинку в четверть волны: если расположить пластинку так, чтобы угол - угол между пл-тью колебаний в падающем луче и осью пластинки). Если пропустить плоскополяризованный свет через пластинку в четверть волны: если расположить пластинку так, чтобы угол 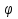 между пл-тью колебаний Р в падающем луче и осью пластинки О равняться π / 4 , амплитуды обоих лучей, вышедших из пластинки, будут одинаковы. Свет вышедший из пластинки, будет поляризован по кругу. При ином значение угла между пл-тью колебаний Р в падающем луче и осью пластинки О равняться π / 4 , амплитуды обоих лучей, вышедших из пластинки, будут одинаковы. Свет вышедший из пластинки, будет поляризован по кругу. При ином значение угла 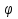 амплитуды вышедших из пластинки лучей будут неодинаковыми. Поэтому при наложении эти лучи образуют свет, поляризованный по эллипсу, одна из осей которого совпадает с осью пластинки О. амплитуды вышедших из пластинки лучей будут неодинаковыми. Поэтому при наложении эти лучи образуют свет, поляризованный по эллипсу, одна из осей которого совпадает с осью пластинки О. |
