Физика Теория. 1. Электромагнитная природа света. Сложение колебаний, понятие о когерентности. Интерференция световых волн. Расчет интерференционной картины от двух источников.
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
^15м. Соотношение неопределенностей Гейзенберга. Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства частиц и все свойства волн нельзя. В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927 г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (рх, ру, рг), причем неопределенности этих величин удовлетворяют условиям, т.е. произведение координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h. Из соотношения неопределенностей следует, что, например, если микрочастица находится в состоянии с точным значением координаты ( 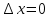 ) то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной ) то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной  и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам. и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
Немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая 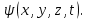 Эту величину называют также волновой функцией (или Эту величину называют также волновой функцией (или 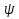 -функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля: -функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля: 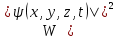 - функция , комплексно сопряженная с - функция , комплексно сопряженная с 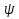 ). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами ). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами 
При движении свободной частицы (U(x) = 0) ее полная энергия совпадает с кинетической. Для свободной частицы, движущейся вдоль оси х, уравнение Шредингера для стационарных состояний примет вид 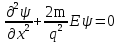 .Прямой подстановкой можно убедиться в том, что частным решением уравнения i является функция .Прямой подстановкой можно убедиться в том, что частным решением уравнения i является функция 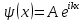 , где A=const и k = const, с собственным значением энергии , где A=const и k = const, с собственным значением энергии 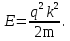 Функция Функция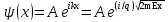 представляет собой только координатную часть волновой функции представляет собой только координатную часть волновой функции 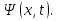 Поэтому зависящая от времени волновая функция, согласно Поэтому зависящая от времени волновая функция, согласно 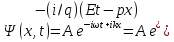 , (219.3) (здесь , (219.3) (здесь  Функция представляет собой плоскую монохроматическую волну де Бройля). Из выражения Функция представляет собой плоскую монохроматическую волну де Бройля). Из выражения 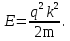 следует, что зависимость энергии от импульса следует, что зависимость энергии от импульса 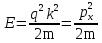 оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным. Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства. оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным. Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства.
8. Излучение и поглощение электромагнитной волны. Спонтанное и вынужденное излучение. Резонансное поглощение. Ширина спектральной линии. Коэффициенты Эйнштейна.
Пусть 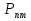 — вероятность вынужденного перехода атома в единицу времени с энергетического уровня — вероятность вынужденного перехода атома в единицу времени с энергетического уровня 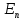 на уровень на уровень  , а , а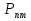 — вероятность обратного перехода. Выше было указано, что при одинаковой интенсивности излучения — вероятность обратного перехода. Выше было указано, что при одинаковой интенсивности излучения 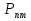 = =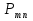 . Вероятность вынужденных переходов пропорциональна плотности энергии «и вынуждающего переход электромагнитного поля), приходящейся на частоту . Вероятность вынужденных переходов пропорциональна плотности энергии «и вынуждающего переход электромагнитного поля), приходящейся на частоту 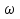 , соответствующую данному переходу , соответствующую данному переходу 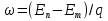 .Обозначив коэффициент пропорциональности буквой В, получим .Обозначив коэффициент пропорциональности буквой В, получим  . В е л и ч и н ы . В е л и ч и н ы 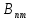 и и 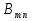 н а з ы в а ю т с я к о э ф ф и ц и е н т а м и Э й н ш т е й н а . Согласно сказанному выше н а з ы в а ю т с я к о э ф ф и ц и е н т а м и Э й н ш т е й н а . Согласно сказанному выше 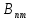 = = 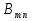 . Основываясь на равновероятности вынужденных переходов п-т и т-п, Эйнштейн дал весьма простой вывод формулы Планка. Равновесие между веществом и излучением будет достигнуто при условии, что число атомов . Основываясь на равновероятности вынужденных переходов п-т и т-п, Эйнштейн дал весьма простой вывод формулы Планка. Равновесие между веществом и излучением будет достигнуто при условии, что число атомов 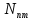 , совершающих в единицу времени переход из состояния п в состояние т, будет равно числу атомов , совершающих в единицу времени переход из состояния п в состояние т, будет равно числу атомов 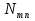 , совершающих переход в обратном направлении. Допустим, что , совершающих переход в обратном направлении. Допустим, что 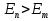 .Тогда переходы т-п смогут происходить только под воздействием излучения. Переходы же m-n будут совершаться как вынужденно, так и спонтанно. .Тогда переходы т-п смогут происходить только под воздействием излучения. Переходы же m-n будут совершаться как вынужденно, так и спонтанно.Лазеры._Рубиновый_и_гелий-неоновый_лазеры.'>9. Квантовое усиление и генерация света. Инверсная населенность уровней (методы осуществления инверсии населенностей). Лазеры. Рубиновый и гелий-неоновый лазеры.
Для того чтобы получить усиление падающей волны, нужно (обратить населенность энергетических уровней, т. е. сделать так, 'чтобы в состоянии с большей энергией 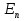 находилось большее число атомов, чем в состоянии с меньшей энергией находилось большее число атомов, чем в состоянии с меньшей энергией 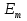 . В этом случае говорят, что данная совокупность атомов имеет инверсную населенность. Согласно формуле . В этом случае говорят, что данная совокупность атомов имеет инверсную населенность. Согласно формуле 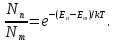 В случае инверсной населенности В случае инверсной населенности 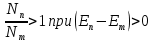 .Распространив формально на этот случаи распределение (,43.1), мы получим для Г отрицательное значение. Поэтому состояния с инверсной населенностью называют иногда состояниями с отрицательной температурой. Изменение интенсивности света при прохождении через поглощающую среду описывается формулой .Распространив формально на этот случаи распределение (,43.1), мы получим для Г отрицательное значение. Поэтому состояния с инверсной населенностью называют иногда состояниями с отрицательной температурой. Изменение интенсивности света при прохождении через поглощающую среду описывается формулой 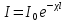 .В веществе с инверсной населенностью энергетических уровней вынужденное излучение может превысить поглощение света атомами, вследствие чего падающий пучок света при прохождении через вещество будет усиливаться. В случае усиления падающего пучка явление протекает так, как если бы коэффициент поглощения и в формуле .В веществе с инверсной населенностью энергетических уровней вынужденное излучение может превысить поглощение света атомами, вследствие чего падающий пучок света при прохождении через вещество будет усиливаться. В случае усиления падающего пучка явление протекает так, как если бы коэффициент поглощения и в формуле 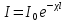 стал отрицательным. Соответственно совокупность атомов с инверсной населенностью можно рассматривать как среду с отрицательным коэффициентом поглощения. стал отрицательным. Соответственно совокупность атомов с инверсной населенностью можно рассматривать как среду с отрицательным коэффициентом поглощения.
Практически инверсное состояние среды осуществлено в принципиально новых источниках излучения — оптических квантовых генераторах, или лазерах (от первых букв английского названия Light Amplification by Stimulated Emission of Radiation — усиление света с помощью вынужденного излучения). Лазеры генерируют в видимой, инфракрасной и ближней ультрафиолетовой областях (в оптическом диапазоне). Идея качественно нового принципа усиления и генерации электромагнитных волн, примененная в мазерах (генераторы и усилители, работающие в сантиметровом диапазоне радиоволн) и лазерах, принадлежит советским ученым Н. Г. Басову (р. 1922) и А. М. Прохорову (р. 1916) и американскому физику Ч. Таунсу (р. 1915), удостоенным Нобелевской премии 1964 г. Важнейшими из существующих типов лазеров являются твердотельные, газовые, полупроводниковые и жидкостные (в основу такого деления положен тип активной среды). Более точная классификация учитывает также и методы накачки — оптические, тепловые, химические, электроионизационные и др. Кроме того, необходимо принимать во внимание и режим генерации — непрерывный или импульсный. Лазер обязательно имеет три основных компонента: 1) активную среду, в которой создаются состояния с инверсией населенностей; 2) систему накачки (устройство для создания инверсии в активной среде); 3) оптический резонатор (устройство, выделяющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок).
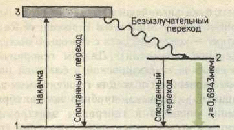 Первым твердотельным лазером (1960; США), работающим в видимой области спектра (длина волны излучения 0,6943 мкм), был рубиновый лазер (Т. Мейман (р,1927)). В нем инверсная населенность уровней осуществляется по трехуровневой схеме, предложенной в 1955 г. Н. Г. Басовым и А. М. Прохоровым. При интенсивном облучении рубина светом мощной импульсной лампы атомы хрома переходят с нижнего уровня на уровни широкой полосы 3 (рис. 310). Так как время жизни атомов хрома в возбужденных состояниях мало (меньше 10-7 с), то осуществляются либо спонтанные переходы 3-1, либо наиболее вероятные безызлучательные переходы на уровень 2 (он называется метастабильным) с передачей избытка энергии решетке кристалла рубина. Переход 2-»-/ запрещен правилами отбора, поэтому длительность возбужденного состояния 2 атомов хрома порядка 10 |

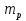 где
где 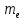 — масса электрона. Нейтрон (n) — нейтральная частица с массой покоя
— масса электрона. Нейтрон (n) — нейтральная частица с массой покоя 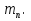 Протоны и нейтроны называются нуклонами (от лат. nucleus — ядро). Общее число нуклонов в атомном ядре называется массовым числом А. Атомное ядро характеризуется зарядом
Протоны и нейтроны называются нуклонами (от лат. nucleus — ядро). Общее число нуклонов в атомном ядре называется массовым числом А. Атомное ядро характеризуется зарядом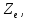 где е — заряд протона, Z — зарядовое число ядра, равное числу прогонов в ядре и совпадающее с порядковым номером химического элемента в Периодической системе элементов Менделеева. Ядро обозначается тем же символом, что и нейтральный атом:
где е — заряд протона, Z — зарядовое число ядра, равное числу прогонов в ядре и совпадающее с порядковым номером химического элемента в Периодической системе элементов Менделеева. Ядро обозначается тем же символом, что и нейтральный атом: 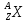 , где X — символ химического элемента, Z — атомный номер (число протонов в ядре), А —массовое число (число нуклонов в ядре). Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. Ядра с одинаковыми Z, но разными А называются изотопами, а ядра с одинаковыми А, но разными Z—изобарами. Радиус ядра задается эмпирической формулой
, где X — символ химического элемента, Z — атомный номер (число протонов в ядре), А —массовое число (число нуклонов в ядре). Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. Ядра с одинаковыми Z, но разными А называются изотопами, а ядра с одинаковыми А, но разными Z—изобарами. Радиус ядра задается эмпирической формулой 
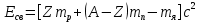 , где
, где 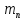 ,
, 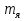 — соответственно массы протона, нейтрона и ядра. В таблицах обычно приводятся не массы ядер, а массы m атомов. Поэтому для энергии связи ядра пользуются формулой
— соответственно массы протона, нейтрона и ядра. В таблицах обычно приводятся не массы ядер, а массы m атомов. Поэтому для энергии связи ядра пользуются формулой 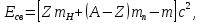
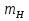 — масса атома водорода. Так как
— масса атома водорода. Так как 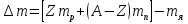 называется дефектом массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них атомного ядра. Часто вместо энергии связи рассматривают удельную энергию связи 6Еп — энергию связи, отнесенную к одному нуклону. Между составляющими ядро нуклонами действуют особые, специфические для ядра силы, значительно превышающие кулоновские силы отталкивания между протонами. Они называются ядерными силами. С помощью экспериментальных данных (рассеяние нуклонов на ядрах, ядерные превращения и т. д.) доказано, что ядерные силы намного превышают гравитационные, электрические и магнитные взаимодействия и не сводятся к ним. Ядерные силы относятся к классу так называемых сильных взаимодействий. Перечислим основные свойства ядерных сил:
называется дефектом массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них атомного ядра. Часто вместо энергии связи рассматривают удельную энергию связи 6Еп — энергию связи, отнесенную к одному нуклону. Между составляющими ядро нуклонами действуют особые, специфические для ядра силы, значительно превышающие кулоновские силы отталкивания между протонами. Они называются ядерными силами. С помощью экспериментальных данных (рассеяние нуклонов на ядрах, ядерные превращения и т. д.) доказано, что ядерные силы намного превышают гравитационные, электрические и магнитные взаимодействия и не сводятся к ним. Ядерные силы относятся к классу так называемых сильных взаимодействий. Перечислим основные свойства ядерных сил: