Физика Теория. 1. Электромагнитная природа света. Сложение колебаний, понятие о когерентности. Интерференция световых волн. Расчет интерференционной картины от двух источников.
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
Кольца Ньютона. Являются классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических окружностей. В отраженном свете оптическая разность хода (с учетом потери половины при отражении), при условии что 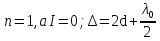 , где d – ширина зазора. , где d – ширина зазора.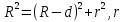 – радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая – радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая . Следовательно, . Следовательно, . . . .Приравняв, к условиям максимума и минимума получим выражения для радиуса m-го светлого и темного колец: Измеряя радиусы соответствующих колец можно (зная радиус кривизны линзы) определить 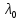 и наоборот, найти радиус кривизны линзы. Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны и наоборот, найти радиус кривизны линзы. Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны 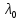 . Поэтому система светлых и темных полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску. Все рассуждения были приведены для отраженного света. Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на . Поэтому система светлых и темных полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску. Все рассуждения были приведены для отраженного света. Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на  . т.е. максимумам интерференции в отраженном свете соответствует минимумы в проходящем, и наоборот. . т.е. максимумам интерференции в отраженном свете соответствует минимумы в проходящем, и наоборот.
В отличие от двулучевой интерференции, многолучевая интерференция возникает при наложении большого числа когерентных световых пучков. Распределение интенсивности в интерференционной картине существенно различается; интерференционные максимумы значительно уже и ярче, чем при наложении двух когерентных световых пучков. Так результирующая амплитуда световых колебаний одинаковой амплитуды в максимумах интенсивности. где сложение происходит в одинаковой фазе, в N раз больше, a интенсивность в  раз больше, чем от одного пучка (N – число интерферирующих пучков).Многолучевую интерференцию можно осуществить в многослойной системе чередующихся пленок с разными показателями преломления (но одинаковой оптической толщиной раз больше, чем от одного пучка (N – число интерферирующих пучков).Многолучевую интерференцию можно осуществить в многослойной системе чередующихся пленок с разными показателями преломления (но одинаковой оптической толщиной 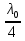 ), нанесенных на отражающую поверхность. На границе раздела пленок возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленки ), нанесенных на отражающую поверхность. На границе раздела пленок возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленки 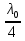 будут взаимно усиливаться, т.е. коэффициент отражения возрастает. Характерной особенностью такой высокоотражательной системы является то, что она действует в очень узкой спектральной области, причем, чем больше коэф-т отражения, тем уже эта область. Для осуществления интерференции многих световых волн с близкими или равными амплитудами применяются спец. приборы – дифракц. решетки. Амплитуду А результирующих колебаний и интенсивность будут взаимно усиливаться, т.е. коэффициент отражения возрастает. Характерной особенностью такой высокоотражательной системы является то, что она действует в очень узкой спектральной области, причем, чем больше коэф-т отражения, тем уже эта область. Для осуществления интерференции многих световых волн с близкими или равными амплитудами применяются спец. приборы – дифракц. решетки. Амплитуду А результирующих колебаний и интенсивность 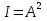 в произвольной точке М интерференционной картины можно найти методом векторных диаграмм. для сложения одинаково направленных колебаний. На рисунке показана векторная диаграмма сложения колебаний при интерференции N волн, возбуждающих в точке М одинаково направленные когерентные колебания с равными амплитудами в произвольной точке М интерференционной картины можно найти методом векторных диаграмм. для сложения одинаково направленных колебаний. На рисунке показана векторная диаграмма сложения колебаний при интерференции N волн, возбуждающих в точке М одинаково направленные когерентные колебания с равными амплитудами 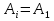 и не зависящим от I сдвигом фаз между (i+1)-м и i-м колебаниями: и не зависящим от I сдвигом фаз между (i+1)-м и i-м колебаниями: 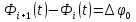 . Амплитуда результирующих колебаний . Амплитуда результирующих колебаний , где , где  . Главные максимумы интерференции N волн наблюдаются в тех точках М, для которых углы . Главные максимумы интерференции N волн наблюдаются в тех точках М, для которых углы  либо равны 0,, либо кратны 2п, так что векторная диаграмма сложения имеет вид Таким образом условие для главных максимумов имеет вид: либо равны 0,, либо кратны 2п, так что векторная диаграмма сложения имеет вид Таким образом условие для главных максимумов имеет вид:  = ±2nπ , где n-порядок главного максимума. Амплитуда и интенсивность колебаний в главных максимумах равны = ±2nπ , где n-порядок главного максимума. Амплитуда и интенсивность колебаний в главных максимумах равны 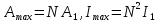 . Интерференционные минимумы (А=0) удовлетворяют условию . Интерференционные минимумы (А=0) удовлетворяют условию 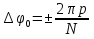 , где р принимает любые целые положительные значения, кроме кратных N. , где р принимает любые целые положительные значения, кроме кратных N.
Явление интерференции используется в ряде весьма точных измерительных приборов, получивших название интерферометров. Также это явление применяется для улучшения качеств оптических приборов (просветление оптики) и получения высокоотражающих покрытий. Например, Прохождение света через каждую преломляющую поверхность линзы, например через границу стекло-воздух, сопровождается отражением порядка 4% падающего потока (при n стекла 1.5). Так как современные объективы содержат большое количество линз, то число отражений в них велико, а поэтому в них велики и потери светового потока. Таким образом интенсивность прошедшего света ослабляется и светосила опт. прибора уменьшается. Кроме того, отражение от поверхности линз приводит к возникновению бликов. Чтобы интерферирующие лучи гасили друг друга их амплитуды должны быть равны, а оптическая разность хода – равна  . . Интерферометры – оптические приборы, основанные на явлении интерференции световых волн. Они получили наибольшее распространение как приборы для измерения длин волн спектральных линий и их структуры; для измерения показателя преломления прозрачных сред; в метрологии для абсолютных и относительных измерений длин и перемещений объектов; измерения угловых размеров звезд; для контроля формы и деформации оптических деталей и чистоты металлических поверхностей. Принцип действия основан на пространственном разделении пучка света с целью получения нескольких когерентных лучей, которые проходят различные оптические пути, а затем сводятся вместе и наблюдается результат их интерференции. 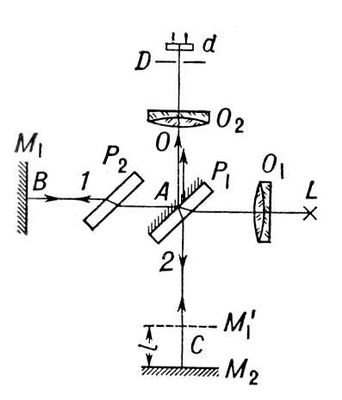 Монохроматический свет от источника L падает под углом 45° на плоскопараллельную пластинку P1. Сторона пластинки, удаленная от L, посеребренная и полупрозрачная, разделяет луч на две части: луч 1 (отражается от посеребренного слоя) и луч 2 (проходит через него). Луч 1 отражается от зеркала М1 и, возвращаясь обратно, вновь проходит через пластинку Р1 (луч 1'). Луч 2 идет к зеркалу М2, отражается от него, возвращается обратно и отражается от пластинки Р1 (луч 2'). Так как первый из лучей проходит пластинку Р1 дважды, то для компенсации возникающей разности хода на пути второго луча ставится пластинка Р2 (точно такая же, как и Р1, только не покрытая слоем серебра). Лучи 1' и 2' когерентны; следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точки О до зеркала М1 и луча 2 от точки О до зеркала M2. При перемещении одного из зеркал на расстояние 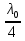 разность хода обоих лучей увеличится на разность хода обоих лучей увеличится на  и произойдет смена освещенности зрительного поля. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр Майкельсона для точного измерения длин. и произойдет смена освещенности зрительного поля. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр Майкельсона для точного измерения длин.2. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля от диска и круглого отверстия. Зонные пластинки. Характерные области дифракции света. Дифракция в параллельных лучах (дифракция Фраунгофера). Дифракция Фраунгофера от щели. Дифракция Фраунгофера на системе щелей. Дифракционная решетка. Дифракционные спектры. Критерий разрешения Рэлея. Дисперсия и разрешающая способность решетки. Дифракция рентгеновских волн.
Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями, например, в близи границ прозрачных или непрозрачных тел, сквозь малые отверстия. Дифракция, в частности, приводит к огибанию световыми волнами препятствий, и проникновению света в область геометрической тени. Между интерференцией и дифракцией нет существенных физических различий. Оба явления заключаются в перераспределении светового потока в рез-тате суперпозиции волн. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, принято называть дифракцией волн. Поэтому говорят, например, об интерференционной картине от двух узких щелей и о дифракционной картине от одной щели. Различают два вида дифракции. Если источник S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку Р, образуют практически параллельные пучки, говорят о дифракции Фраунгофера (дифракции. в параллельных лучах). В противном случае говорят о дифракции Френеля.
Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени. Но этот принцип не дает сведений об амплитуде а следовательно и об интенсивности волн, распространившихся в различных направлениях. Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Согласно принципу Г-Ф каждый элемент волновой поверхности S служит источником вторичной волны, амплитуда которой пропорциональна величине элемента dS. Амплитуда сферической волны убывает с расстоянием по закону 1/r. След. от каждого участка dS волновой поверхности в точку Р, лежащую перед этой поверхностью, приходит колебание 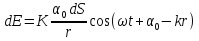 , где , где 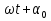 - в месте расположения волновой поверхности S, к – волновое число. Множитель - в месте расположения волновой поверхности S, к – волновое число. Множитель 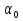 определяется амплитудой светового колебания в том месте, где находится dS. К зависит от определяется амплитудой светового колебания в том месте, где находится dS. К зависит от 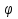 между нормалью n к dS и направлением от dS к Р. При между нормалью n к dS и направлением от dS к Р. При 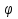 =0, К – максимален, при =0, К – максимален, при 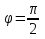 – он обращается в 0. Результирующее колебание в точке Р будет: – он обращается в 0. Результирующее колебание в точке Р будет: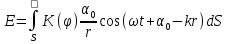 . Эта формула является аналитическим выражением принципа Г-Ф. . Эта формула является аналитическим выражением принципа Г-Ф.
Принцип Г- Ф. должен был ответить на вопрос о прямолинейном распространении света. Френель решил эту задачу, рассмотрев взаимную интерференцию вторичных волн и применив следующий прием: Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде из точечного источника монохроматического света 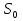 . Согласно принципу Г-Ф. заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся пов-тью фронта волны, идущей из . Согласно принципу Г-Ф. заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся пов-тью фронта волны, идущей из  (пов-ть сферы радиуса R с центром S). Радиус выберем так, чтобы расстояние L от точки М до этой сферы (L=|OM|) было порядка R. (пов-ть сферы радиуса R с центром S). Радиус выберем так, чтобы расстояние L от точки М до этой сферы (L=|OM|) было порядка R.  Разобьем поверхность S на небольшие по площади кольцевые участки – зоны Френеля. Колебания, возбуждаемые в точке М двумя соседними зонами , противоположны по фазе, т.к. разность хода от сходственных точек этих зон до точки М равна  . След. амплитуда результирующих колебаний в точке М: . След. амплитуда результирующих колебаний в точке М: 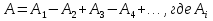 – амплитуда колебаний, возбуждаемых в точке М вторичными источниками. Величина – амплитуда колебаний, возбуждаемых в точке М вторичными источниками. Величина 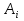 зависит от площади зависит от площади 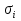 i-той зоны и угла i-той зоны и угла 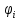 между внешней нормалью к поверхности зоны в какой-либо ее точке и прямой, направленной из этой точки в точку М. Точки В и В’ соответствуют внешне границе i- той зоны. Общее число N зон Френеля, уменьшающихся на части сферы, обращенной к точке М велико: между внешней нормалью к поверхности зоны в какой-либо ее точке и прямой, направленной из этой точки в точку М. Точки В и В’ соответствуют внешне границе i- той зоны. Общее число N зон Френеля, уменьшающихся на части сферы, обращенной к точке М велико: 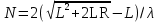 . Например, если . Например, если 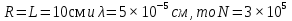 . Радиус зоны определяется по формуле . Радиус зоны определяется по формуле 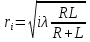 . .
15. Дифракция Френеля от круглого отверстия и от диска. 1. От круглого отверстия. Поставим на пути сферической световой волны (т.е. для которой А убывает как 1/r, r – расстояние,, отсчитываемое вдоль направления распространения световой волны) непрозрачный экран. Расположим его так, чтобы перпендикуляр, опущенный из источника света S, попал в центр отверстия. На продолжении этого перпендикуляра возьмем точку Р. При радиусе отверстия 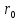 , значительно меньшем, чем указанные на рис. длины a и b, длину a можно считать равной расстоянию от источника S, до преграды, а длину b – от расстояния преграды до Р. Если расстояния а и b удовлетворяют соотношению: , значительно меньшем, чем указанные на рис. длины a и b, длину a можно считать равной расстоянию от источника S, до преграды, а длину b – от расстояния преграды до Р. Если расстояния а и b удовлетворяют соотношению: 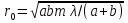 , где m – целое число, то отверстие оставит открытым ровно m первых зон Френеля, построенных для точки Р. Следовательно, число открытых зон будет: , где m – целое число, то отверстие оставит открытым ровно m первых зон Френеля, построенных для точки Р. Следовательно, число открытых зон будет: 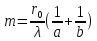 , а амплитуда в точке Р будет равна , а амплитуда в точке Р будет равна 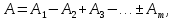 знак минус берется, если m – нечетное и плюс – четное. знак минус берется, если m – нечетное и плюс – четное. 2. Дифракция от круглого диска. 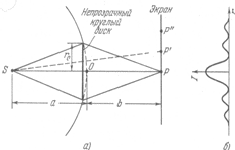 Поместим между источником света S и точкой наблюдения Р непрозрачный диск радиуса 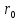 . Если диск закроет m первых зон Френеля, амплитуда в точке Р будет равна: . Если диск закроет m первых зон Френеля, амплитуда в точке Р будет равна: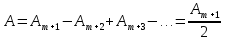 . .
Из теории Френеля (световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками, такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S). следует, что в том случае, когда в отверстии укладывается только одна зона Френеля, амплитуда колебаний в точке М 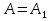 , т.е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием (соответственно интенсивность в точкеM: , т.е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием (соответственно интенсивность в точкеM: 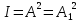 ). Амплитуду А можно значительно увеличить с помощью зонной пластинки – стеклянной пластинки, на поверхность которой так нанесено непрозрачное покрытие, что оно закрывает все четные зоны Френеля и оставляет открытыми все нечетные зоны (либо наоборот). Если общее число зон, уменьшающихся на пластинке, равно 2k, то ). Амплитуду А можно значительно увеличить с помощью зонной пластинки – стеклянной пластинки, на поверхность которой так нанесено непрозрачное покрытие, что оно закрывает все четные зоны Френеля и оставляет открытыми все нечетные зоны (либо наоборот). Если общее число зон, уменьшающихся на пластинке, равно 2k, то 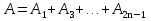 . Если 2k не слишком велико, то . Если 2k не слишком велико, то  и A ≈ k и A ≈ k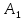 , т.е. освещенность экрана в точке М в k2 раз больше, чем при беспрепятственном распространении света от источника в точку М. Зонная пластинка действует на свет подобно собирающей линзе. , т.е. освещенность экрана в точке М в k2 раз больше, чем при беспрепятственном распространении света от источника в точку М. Зонная пластинка действует на свет подобно собирающей линзе.
Бесконечно длинную щель можно образовать, расположив ряжом две обращенные в разные стороны полуплоскости. Следовательно, задача и дифракции Френеля от щели может быть решена с помощью спирали Карню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу. Для точки Р, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали. Если сместиться в точку Р’, лежащую против края щели, начало результирующего вектора переместится в середину спирали О. Конец вектора переместится по спирали в направлении полюса F1. 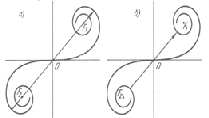   При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (вектор, соответствующий точке Р’’). Интенсивность света при этом достигнет минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки Р в противоположное сторону, так как дифракционная картина симметрична относительно середины щели. Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы (а) и отличные от нуля минимумы (б). |
