электрические и магнитные цепи. 1 электротехнические устройства постоянного тока

• Название: 1 электротехнические устройства постоянного тока
• Анкор: электрические и магнитные цепи.doc
• Дата: 19.08.2018
• Размер: 1.08 Mb.
• Имя файла: электрические и магнитные цепи.doc
• Тип: Документы; #23206
• страница: 3 из 7

ГЛАВА ВТОРАЯ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
2.1. ЭЛЕКТРОТЕХНИЧЕСКИЕ УСТРОЙСТВА СИНУСОИДАЛЬНОГО ТОКА
Электротехнические устройства синусоидального (переменного) тока находят самое широкое применение в различных областях народ­ного хозяйства: при генерировании, передаче и трансформировании электрической энергии, в электроприводе, бытовой технике, промыш­ленной электронике, радиотехнике и т. д. Преимущественное распро­странение электротехнических устройств синусоидального тока обу­словлено рядом причин.

Современная энергетика основана на передаче энергии на дальние расстояния при помощи электрического тока. Обязательным условием передачи электроэнергии на дальние расстояния и ее распределения является возможность применения простого и с малыми потерями энергии преобразования тока. Такое преобразование осуществимо лишь в электротехнических устройствах переменного тока — транс­форматорах. Вследствие громадных преимуществ трансформирования в современной электроэнергетике и применяется прежде всего сину­соидальный ток. Исключение составляют лишь линии передачи постоянного тока сверхвысокого напряжения и некоторые технологические установки, но и они входят составной частью в систему цепей сину­соидального тока.

Большим стимулом для разработки и развития электротехнических устройств синусоидального тока является возможность получения источников электрической энергии большой мощности. У современных турбогенераторов тепловых электростанций мощность равна 100— 1500МВт на один агрегат. Большие мощности имеют и генераторы гидростанций.

К наиболее простым и дешевым электрическим двигателям отно­сятся асинхронные двигатели синусоидального тока, в которых отсут­ствуют движущиеся электрические контакты.

Для электроэнергетических установок (в частности, для всех электрических станций) в РФ и в большинстве стран мира принята стандартная частота 50 Гц(в США — 60 Гц). Причины такого выбора простые: понижение частоты неприемлемо, так как уже при частоте тока 40 Гц лампы накаливания заметно для глаза мигают; повышение частоты нежелательно, так как пропорционально частоте растет ЭДС самоиндукции, отрицательно влияющая на передачу энергии по про­водам и работу многих электротехнических устройств.
1.2. ЭЛЕМЕНТЫ ЭЛЕКТРИЧЕСКОЙ

ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Электрическая цепь синусоидального тока содержит помимо элек­тротехнических устройств, назначение которых совпадает с назначе­нием функционально аналогичных устройств цепи постоянного тока (источники энергии, измерительные приборы, коммутационные аппа­раты и т. д.), также устройства, присущие только цепям синусоидального тока: трансформаторы, конденсаторы, катушки индуктивности и др. Всю совокупность электротехнических устройств в цепи синусои­дального тока для наглядного и компактного отображения связей между ними можно представить принципиальной схемой, аналогичной показанной на рис. 1.2

Для расчета режима работы электротехнических устройств необхо­димо перейти от принципиальной схемы цепи к ее схеме замещения, которая является количественной моделью для описания процессов в цепи. Схема замещения цепи получается из принципиальной схемы цепи, если все электротехнические устройства представлены соответ­ствующими схемами замещения, состоящими из идеализированных элементов, каждый из которых с достаточно хорошим приближением описывает процессы в той или иной части реального устройства. Напря­жения и токи в электрических цепях синусоидального тока и в схемах замещения, соответствующие различным моментам времени, а также в других электрических цепях, в которых токи и напряжения зависят от времени, называются мгновенными значениями и обозначаются строчными буквами ( н и.

Элементами схем замещения цепей синусоидального тока являются источники синусоидального тока, источники синусоидальной ЭДС, резистивные, индуктивные и емкостные элементы. Понятия об источ­никах тока и ЭДС, а также резистивных элементах уже были рассмот­рены при анализе цепей постоянного тока. Индуктивные и емкостные элементы являются специфическими элементами при анализе электри­ческих цепей синусоидального тока.

Если параметры элементов не зависят от тока и приложенного к ним напряжения, то это линейные элементы. В противном случав элементы следует считать нелинейными.
2.2 ИНДУКТИВНЫЙ ЭЛЕМЕНТ
Вокруг всякого проводника с током г существует, магнитное поле. В электротехнических устройствах синусоидального тока, например в трансформаторах, электрических двигателях, катушках измеритель­ных приборов и т. д. необходимо создавать сильные магнитные поля.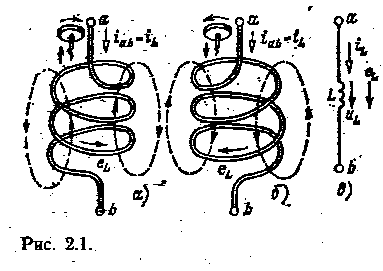






Свойства изменяющегося магнитного поля таких устройств рассмотрим на примере катушек индуктивности с различным на­правлением намотки и не будем учитывать сопротивление прово­дов обмотки. Если ток i_аЬ = i_l . в катушке постоянный, то в ок­ружающем витки пространстве постоянно и магнитное поле, ко­торое можно характеризовать магнитным потоком Ф—совокупностью непрерывных магнитных линий, т. е. линий вектора индукции В че­рез поверхность, ограниченную замкнутым контуром. Направление магнитных линий зависит от направления намотки витков и направ­ления тока. Внутри катушки оно совпадаете направлением движения буравчика, если его рукоятку вращать в направлении тока (рис. 2.1, и и б). В общем случае конфигурация магнитного поля вокруг витков имеет сложную форму. Но для характеристики катушки ин­дуктивности как элемента электрической цепи часто не требуется знать распределение магнитного поля в окружающем катушку прос­транстве. Достаточно вычислить потокосцепление ¥ магнитного по­тока со всеми w витками:

¥=Ф₁+Ф₂+…+Ф_R+…+Ф_w=∑^w_R=1 Ф_R

где ф_R — магнитный поток, сцепленный с R-м витком.

Основной единицей потокосцепления и магнитного потока в системе СИ служит вебер (Вб).

Так как в рассматриваемом случае потокосцепление с витками катушки зависит от тока в этой же катушке, оно называется собствен­ным потокосцеплением.

Если со всеми витками катушки сцеплен одинаковый магнитный поток Ф, то собственное потокосцепление

¥=wФ

Отношение собственного потокосцепления катушки к току (_ай =-(_Е катушки называется собственной индуктивностью или короче индук­тивностью:

L=¥/i_L (2.1)

Если собственное потокосцепление пропорционально току, то индук­тивность I =-сопз1. В противном случае индуктивность зависит от тока /, (4). Зависимость индуктивности от тока проявляется, напри­мер, у катушек индуктивности с магнитопровбдом.

Так как электрическому току всегда сопутствует магнитное поле, параметром каждой части электротехнического устройства, в которой есть ток, должна быть индуктивность. Конечно, в ряде случаев эта индуктивность может быть настолько мала, что ее влиянием можно пре­небречь.

Основной единицей индуктивности в системе СИ является генри

(Гн), 1 Гн = 1 Вб/А.

Индуктивность 1 Гн — достаточно большая единица, поэтому на практике часто применяют кратные единицы измерения индуктивности: миллигенри (мГн), 1 мГн = 1 -10^-3 Гн.

Если значение тока в витках 'катушки изменяется (увеличивается или уменьшается), то изменяется я собственное потокосцепление. При изменении потокосцепления в витках катушки согласно закону электромагнитной индукциинаводится ЭДС самоиндукции е_LУслов­ное положительное направление ЭДС самоиндукции совпадаете направ^ лением вращения рукоятки буравчика, ввинчивающегося по направле­нию магнитных линий, и с выбранным положительным направлением тока (рис. 2.1, а и б). По определению эта ЭДС

е_L=-d¥/dt (2.2а)

или с учетом (2.1)

е_L=-Ldi_l/dt (2.2б)
Из (2.2) следует, что действительное направление ЭДС самоиндук­ции в данный момент времени может отличаться от выбранного поло­жительного направления и определяется знаком производной тока по времени.

Нетрудно видеть, что ЭДС самоиндукции всегда препятствует изменению тока (правило Ленца).

Для того чтобы в катушке индуктивности был переменный ток, между ее выводами должно быть напряжение, равное по значению и в каждый данный момент времени противоположное по направлению ЭДС самоиндукции (рис. 2.1, в):

u_аь = u₁ = — е_L = L di_l/dt=d¥/dt (2.3)

Из выражения (2.3) следует, что основная единица потокосцепления и магнитного потока 1 Вб — 1 В -с, а основная единица индуктивности 1 Гн = 1В-с/А = 1 Ом-с.

Если сопротивлением проводов катушки индуктивности пренебречь нельзя, то к ее схеме замещения по рис. 2.1, в необходимо добавить последовательно включенный резистив-ный элемент.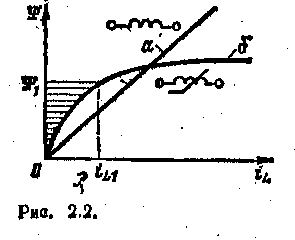






Индуктивность L, является парамет­ром линейных индуктивных элементов, а линейный индуктивный элемент — схемой замещения любой части элек­тротехнического устройства, в которой собственное потокосцепление пропорци­онально току. Если зависимость соб­ственного потокосцепления от тока нели­нейна, то и схема замещения содержит нелинейный индуктивный элемент, ко­торый задается нелинейной вебер-амперной характеристикой ¥ (i_l). На рис. 2.2 приведены вебер-амперные характеристики линейного (а) и нелинейного (б) индуктивных элементов, а также условные обозна­чения таких элементов в схемах замещения соответствующих участков электротехнических устройств.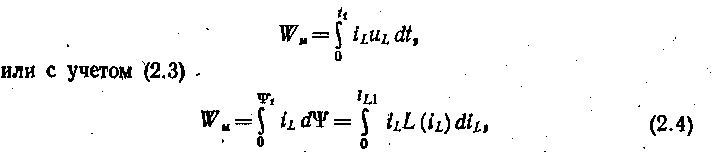




Если за время t₁ ток в индуктивном элементе изменится от нуля до 1ц, то в магнитном поле элемента (рис. 2.1, в) будет запасена энергия

где ¥₁— значение собственного потокосцепления при токе 1₁ = 1_и(рис. 2.2).

Как следует из (2.4), энергия, запасенная в магнитном поле индук­тивного элемента при токе i_lпропорциональна соответствующей площади, заключенной между вебер-амперной характеристикой и осью ординат (рис. 2.2), где заштрихована площадь, пропорциональная энергии магнитного поля нелинейного индуктивного элемента при токе (i_L1).

Из (2.4) с учетом (2.1) следует, что у линейного индуктивного элемента при токе i_L энергия магнитного поля

W_м = Li_L²/2=¥i_L /2. (2.5)

При увеличении (уменьшении) тока энергия магнитного поля индук­тивных элементов увеличивается (уменьшается). Следовательно, индук­тивные элементы можно рассматривать как аккумуляторы энергии, которая может в них накапливаться.
2.3 ЕМКОСТНЫЙ ЭЛЕМЕНТ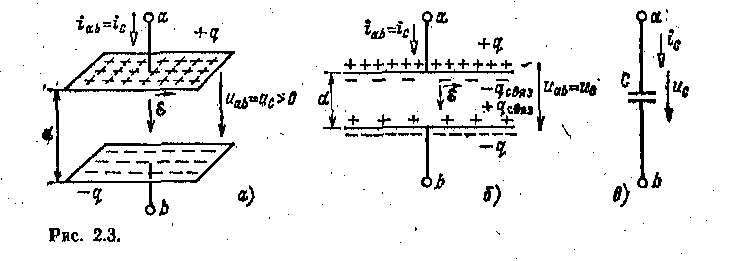



Между различными частями электротехнических устройств сущест­вует электрическое поле электрических зарядов, находящихся на этих частях устройств. В различных электротехнических устройствах, например в изоляторах, конденсаторах и т. д.) возникают достаточно сильные электрические поля.

На рис. 2.3, а изображен простейший плоский конденсатор с двумя параллельными обкладками площадью S, которые находятся в вакууме на расстоянии d друг от друга. Если между верхней и нижней обклад­ками конденсатора площадью S приложить напряжение U_аb > О, то на верхней и нижней обкладках конденсатора накопятся одинаковые положительный и отрицательный заряды ± q, которые называют свободными.

Между обкладками плоского конденсатора электрическое поле будет однородным (если не учитывать краевого эффекта) с напряжен­ностью

ξ=U_ab/d=q/ έ₀S (2.6)

где е₀ = 8,854 -10-¹² Ф/м — электрическая постоянная.

Накопленный (в конденсаторе) заряд q пропорционален приложен­ному напряжению U_аb = U_с

q=Cu_ab= Cu_c (2.7)

коэффициент пропорциональности С называется емкостью конденса­тора.

Решив совместно ««отношения (2.6) и (2.7), получим выражения для емкости плоского вакуумного конденсатора:

С = έ₀ S/d

Для увеличения емкости плоского конденсатора пространство между обкладками заполняется каким-либо диэлектриком (рис. 2.3, б).

Под действием электрического поля хаотически ориентированные в пространстве дипольные молекулы диэлектрика приобретают преиму­щественное направление ориентации. При этом внутри однородного диэлектрика положительные и отрицательные заряды дипольных молекул компенсируют друг друга, а на границах с обкладками плое­ного конденсатора остаются нескомпенсированные слои связанных зарядов а на границе с обкладкой, заряженной положительно, располагается слой отрицательных связанных зарядов, а на границе с обкладкой, заряженной отрицательно, — слой положительных свя­занных зарядов. Наличие связанных зарядов уменьшает напряжен­ность $ электрического поля внутри конденсатора:







откуда следует, что при той же напряженности электрического поля, а следовательно, и напряжении U_аb = U_с заряд q должен быть больше. Поэтому увеличится, как следует из (2.7), и емкость плоского конден­сатора по сравнению с емкостью такого же вакуумного конденсатора:

С = έ_r έ₀S/d, (2.8)

где έ_r — относительная диэлектрическая, проницаемость заполняю­щего конденсатор диэлектрика (безразмерная величина).

Произведение относительной диэлектрической проницаемости έ_r на электрическую постоянную έ₀ называется абсолютной диэлектри­ческой проницаемостью.

έ_а = έ_r έ₀. (2.9)

В табл. 2.1 приведены параметры некоторых диэлектриков.

Если свободный заряд (на пластинах конденсатора) пропорциона­лен напряжению между пластинами, то емкость конденсатора постоян­на: С = const. В противном случае емкость конденсатора зависит от напряжения С (u_с).

Основной единицей емкости в системе СИ является фарой (Ф), 1 Ф = 1 Кл/В = 1 А-с/В. Емкость 1 Ф очень велика. В электротех­нической практике обычно используются дольные единицы емкости: микрофарад (мкФ), I мкФ =1 *^10-6 Ф, нанофарад (нФ), 1 нФ = 1*10^-9Ф, и пнкофарад (пФ), 1 пФ = 1 -10-¹² Ф.

На рис. 2.3, в приведена схема замещения конденсатора (рис. 2.3, о и б) в виде линейного емкостного элемента с параметром С. Такую схему замещения имеет идеальный конденсатор, т. е. конденсатор, у которого можно пренебречь приводящими к нагреванию потерями диэлектрике и изоляции вводов, металле обкладок и т. д. В противном случае в схеме замещения должен быть и резистивнын элемент.
Таблица 2.1. Диэлектрическая проницаемость (относительная), электрическая

прочность и удельное объемное сопротивление некоторых материалов

Наименование вещества	ег	6„ мв/"*	су. Ом-и
Трансформаторное масло	2.1—2,4	15— '20	Ю14— (0и
Совол	4.8-5	Н— 18	К)»— 10»
Вазелин	2,2—2.6	'20—25	5- 101г— 10«
Полиэтилен	2,2—2,4	35—60	1 О*— ЮЧ
Лавсан	3,0— 3,5	80—120	10»— !0">
Полиаиядлхлоркд (плаетнкаты)	6—8	6—15	101»— Юи
Парафин	2.0—2,2	22—32	10»— Ю"
Эбонит	3,0—3,5	15—20	1012—Ю"
Гетинакс	6-8	20-^0	10»— 10"
Слюда (мусковит)	6,5—7,2	98—175	1012—ЮЧ
Мрамор	8—9	1,0—4,0	10'— 10»
Шифер	6-8	0,5—1,5	]0в-,10!
Аебестодемеет	6-8	2,0—3,0	100—103

* Электрическая прочность всех материалов указана для действующего значения переменного напряжения (си. 5 2.6).

Так как электрическое поле всегда существует между различными деталями электротехнических устройств, находящихся под напряже­нием, между этими деталями есть емкость. Конечно, в ряде случаев эта емкость настолько мала, что ее влиянием можно пренебречь.

Линейный емкостный элемент (рис. 2.3, в) является схемой заме­щения любой части электротехни­ческого устройства, если значение заряда пропорционально напряже­нию. Если же заряд не пропорцио­нален напряжению, то схемой заме­щения будет нелинейный емкостный элемент, который задается нелиней­ной кулон-вольтной характеристикой

q (u_c).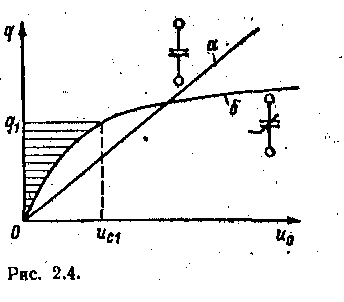






На рис. 2.4 приведены кулон-воль-тные характеристики линейного (а) и

нелинейного (б) емкостных элементов, а также условные обозначения таких элементов на схемах замещения.

Если напряжение, приложенное к емкостному элементу, будет изменяться (увеличиваться или уменьшаться), то будет изменяться и заряд, т. е. в емкостном элементе появится ток. Положительное на­правление тока в емкостном элементе выберем совпадающим с.поло­жительным направлением напряжения, приложенного к емкостному элементу. При этом ток

I_ab=i_c=dq/dt (2.10)

В линейном емкостном элементе с учетом (2.7) ток

I_c=Cdu_c/dt (2.11)
Если за время t₁напряжение на емкостном элементе изменится от нуля до u_c1то в электрическом поле элемента будет накоплена энергия


Или с учетом (2.10)

(2.12)

где q₁ — свободный заряд при напряжении u_с = u_с1 (рис. 2.4).

Как следует из (2.12), энергия, запасенная в электрическом поле емкостного элемента при напряжении u_с, пропорциональна соответ­ствующей площади, заключенной между кулон-вольтной характерис­тикой и осью ординат (рис. 2.4, где заштрихована площадь, пропор­циональная энергии электрического поля нелинейного емкостного элемента при напряжении ис,).

Из (2.12) с учетом (2.7) следует, что у линейного емкостного эле­мента при напряжении u_с энергия электрического поля

W_и=Cu²c/2=qu_c/2 (2.13)

Приведенный анализ показывает, что емкостные элементы электри­ческих цепей можно, как и индуктивные элементы, рассматривать в качестве аккумуляторов энергии, в которых может накапливаться энергия.