электрические и магнитные цепи. 1 электротехнические устройства постоянного тока

• Название: 1 электротехнические устройства постоянного тока
• Анкор: электрические и магнитные цепи.doc
• Дата: 19.08.2018
• Размер: 1.08 Mb.
• Имя файла: электрические и магнитные цепи.doc
• Тип: Документы; #23206
• страница: 4 из 7

Таблица 2.2. Условные графические обозначения катушек индуктивности и конденсаторов




В табл. 2.2 приведены некоторые условные графические обозначе­ния катушек индуктивности и конденсаторов.

В дальнейшем при анализе линейных электрических цепей сину­соидального тока термин «линейный» дополнительно оговариваться не будет.
2.4 ИСТОЧНИКИ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ СИНУСОИДАЛЬНОГО ТОКА
Промышленными источниками синусоидального тока являются электромеханические генераторы, в которых механическая энергия паровых или гидравлических турбин преобразуется в электрическую. Конструкция и работа промышленных электромеханических генера­торов будет подробно рассмотрена в дальнейшем. Здесь ограничимся лишь анализом принципа работы такого генератора при некоторых упрощающих допущениях. Принципиальная конструкция простей­шего электромеханического генератора изображена на рис. 2.5, а. Она содержит неподвижный, плоский разомкнутый виток с выводами а и Ъ и постоянный магнит, который вращается с постоянной частотой f, т. е. с постоянной угловой, частотой w= 2пf, рад/с, внутри витка.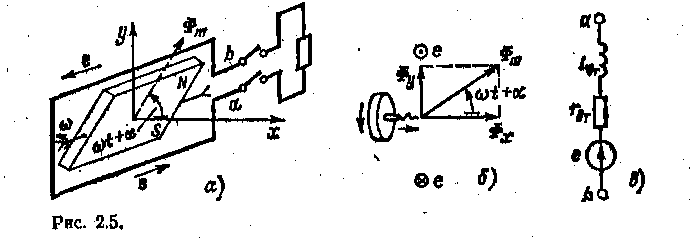





Основной единицей частоты в системе СИ является герц (Гц), 1 Гц = 1 с-¹. В различных областях применения синусоидальных токов часто используются кратные единицы частоты: килогерц (кГц), 1 кГц = = 1*10³ Гц, и мегагерц (МГц), 1 МГц = 1 • 10⁶ Гц. Величина, обратная частоте, называется периодом Т = 1/f, который измеряется в секундах.

Пусть магнитный поток постоянного магнита равен Ф_m. Из про­странственного распределения магнитного потока (рис. 2.5, б) следует, что мгновенное значение составляющей магнитного потока, пронизы­вающей виток, т. е. направленной вдоль оси х, равно:

Ф_х=ф_mcos(wt+a)= ф_msin(wt+¥_ф) (2.14)

где Ф_m — максимальное значение (амплитуда) магнитного потока, пронизывающего виток; а. — начальный (т. е. в момент t = 0 приня­тый за начало отсчета времени) угол пространственного расположения постоянного магнита относительно оси х; ¥_ф = п/2 + а — начальная фаза магнитного потока; wt+¥_ф — фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной функции в момент времени t = 0.

Согласно закону электромагнитной индукции при изменении потоко-сцепления витка в нем индуктируется ЭДС, положительное направле­ние которой (рис. 2.5, а) связывают с положительным направлением потока Ф_хправилом буравчика (положительное направление ЭДС совпадаете направлением вращения рукоятки буравчика, ввинчиваю­щегося в направлении магнитного потока Ф_х). ЭДС индукции

E=-dф_x/dt=-ф_mwcos(wt+¥_ф)=E_msin(wt+¥_e) (2.15)

где Е_т = wф_mфаза ЭДС.— амплитуда ЭДС; ¥_e =¥_ф-п/2=а — начальная фаза ЭДС.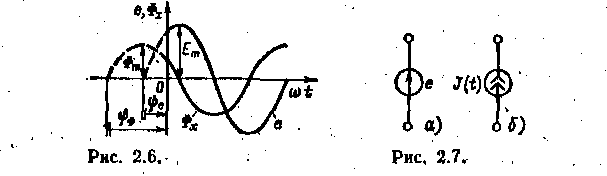




На рис. 2.6 изображены зависимости магнитного потока Ф_х- = = Ф_х (wt)и ЭДС е = е (wt) от фазы wt, т. е, времени t. Заметим, что синусоидальные величины принято изображать графиками в виде зависимостей от wt. Поэтому начальная фаза определяет смещение синусоидальной величины. относительно начала координат, т. е. wt = 0. Начальная фаза всегда отсчитывается вдоль оси абсцисс от ближайшего к началу координат нулевого значения синусоидальной величины при ее переходе от отрицательных значений к положительным до начала координат. Если начальная фаза больше (меньше) нуля, то начало синусоидальной величины сдвинуто влево, как на рис. 2.6, или вправо от начала координат.

Если к выводам а и Ь генератора подключить резистор (рис. 2.5, а), то в полученной цепи возникает синусоидальный ток I.

На рис. 2.5, в приведена схема замещения электромеханического генератора, в которой резистивнын элемент L_вт и индуктивный элемент r_вт отображают внутренние параметры генератора: сопротивление проводов витка и индуктивность витка.

Если параметрами резистивного и индуктивного элементов в схеме замещения генератора можно при расчете тока в цепи пренебречь, то его схемой замещения будет идеальный источник синусоидальной ЭДС (рис. 2.7, а). Если ток в цепи генератора практически не зависит от параметров внешней цепи, то схемой замещения генератора будет идеальный источник синусоидального тока J(t) (рис. 2.7, б), где J (t) = i_К — ток генератора при коротком замыкании его выводов а и Ь.

Промышленный генератор синусоидального тока состоит из непо­движной части — статора [Stator (лат.) — стоящий! и вращающейся части — ротора [Rоtог (лат.) — вращающийся]. Статор собирается из листовой электротехнической стали. Он имеет форму полого цилин­дра (рис. 2.8). В пазах, сделанных вдоль внутренней поверхности ста-

тора, уложены изолированные провода, определенным образом соеди­ненные между собой и образующие обмотку статора, в которой индук­тируется синусоидальная ЭДС. Ротор представляет собой электромаг­нит, возбуждаемый постоянным током. Источником тока возбуждения является возбудитель — небольшой гене­ратор постоянного тока, который соеди­няется с обмоткой ротора через контак­тные кольца, укрепленные на валу ро­тора, и неподвижные щетки.

Одному обороту двухполюсного (N и S) ротора соответствует один период Синусоидальной ЭДС, индуктируемой в проводах обмотки статора. Если же ста­тор имеет р пар полюсов, то одному обо­роту ротора соответствуют р периодов синусоидальной ЭДС. Если частота вра­щения ротора n оборотов в минуту, то ЭДС генератора будет иметь рn периодов в минуту. Частота синусо­идальной ЭДС, т. е. число периодов в секунду: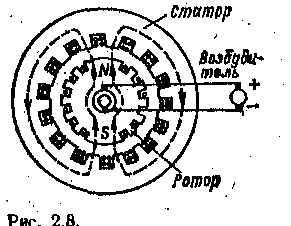




Рис 2.8

f=pn/60
2.5 МАКСИМАЛЬНОЕ, СРЕДНЕЕ И ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЯ СИНУСОИДАЛЬНЫХ ЭДС. НАПРЯЖЕНИЙ И ТОКОВ
В линейной цепи при действии синусоидально изменяющейся ЭДС напряжения и токи также синусоидальные:

U=U_msin(wt+¥_u)

i=I_msin(wt+¥_i)
где w — угловая частота; ¥_u и ¥_i; — начальные фазы напряжения и тока; U_m и I_m- — максимальные значения (амплитуды) напряжения и тока.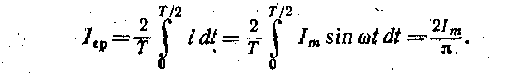




Средним значением синусоидальной величины (ЭДС, тока, напря­жения) считают ее среднее значение за положительный полупериод, совпадающее со средним значением по модулю. Например, для тока вычислим среднее значение, выбрав начальную фазу равной нулю:

Аналогично для ЭДС и напряжения

Е_ср=2Е_m/п U_ср=2U_m/п (2.16б)

Синусоидальный ток в резистивном элементе с сопротивлением г вызывает нагрев этого элемента из-за выделения тепловой энергии. Такую же тепловую энергию в этом же резистивном элементе можно получить при некотором постоянном токе. Определенное посредством такого сравнения значение постоянного тока называется действующим

значением соответствующего синусоидального тока. Например, если синусоидальный ток нагревает некоторый резистивный элемент так же, как его нагрел бы постоянный ток 5 А, то действующее значение сину­соидального тока равно 5 А,

При синусоидальном токе за один период Т в резистивном элементе с сопротивлением г выделяется тепловая энергия, Дж:


где I — мгновенное значение синусоидального тока.

Согласно определению действующего значения синусоидального тока такое же количество тепловой энергии в том же резистивном

элементе должно выделяться при постоян­ном токе за тот же интервал времени Т:





следовательно,





откуда находим искомое действующее значение" синусоидального тока:

Таким образом, действующее значение синусоидального тока опре­деляется как среднее квадратичное за период. На рис. 2.9 показаны синусоидальный ток i, изменение во времени квадрата тока i² и графическое определение значения I²(из равенства площадей I²T=i²dt), а тем самым и действующего значения I.

Для синусоидального тока нетрудно определить действующее зна­чение через амплитудное:






и так как
Следовательно, действующее значение синусоидального тока меньше его амплитуды в  раз.

Аналогично определяется действующее значение синусоидального напряжения. Тепловая энергия, выделяемая в резистивном элементе с проводимостью q = 1 /г за время Т при постоянном напряжении,

Q_теп=qU²T

при синусоидальном напряжения



На основании сопоставления этих двух выражений определяется действующее значение синусоидального напряжения:

U=U_m/ (2,186)

Аналогично для любой другой синусоидальной величины (ЭДС, магнитного потока, заряда и т.д.) действующее значение

А = А_m (2-19)

Действующее значение выбрано в качестве основной характерис­тики синусоидального тока потому, что в большом числе случаев дей­ствие тока пропорционально квадрату этого значения, например тепло­вое действие и сила взаимодействия прямого и обратного проводов двухпроводной линии. Электроизмерительные приборы ряда систем (тепловые, электродинамические, электромагнитные и электростати­ческие) пригодны для измерения как постоянного, так и синусоидаль­ного токов; проградуированные при постоянном токе и включенные в цепь синусоидального тока, они показывают действующее значение последнего.

При расчете изоляции важно учесть, что дважды в течение периода мгновенное значение синусоидального напряжения больше действую­щего значения в раз. Следовательно, изоляция в установке синусо­идального тока находится в менее благоприятных условиях, чем изоля­ция в аналогичной установке постоянного тока. Это одна из причин, по которым для сверхдальних передач электроэнергии в настоящее время стремятся применять постоянный ток высокого напряжения (проектируются линии передачи с напряжением 1500 кВ).
2.6. РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН
Известно несколько способов представления величин, изменяющих­ся по синусоидальному закону: в виде тригонометрических функций, в виде графиков изменений функций во времени, в виде вращающихся векторов и, наконец, в виде комплексных чисел.

В § 2.4 и 2.5уже применялись представления синусоидально изме­няющихся величин в виде тригонометрических функций, например (2.14), (2.15), и в виде графика изменений функций во времени (рис. 2.6).

Теперь рассмотрим представление величин, изменяющихся по синусоидальному закону, в виде вращающихся векторов и комплекс­ных чисел.

Представление синусоидальных величин вращающимися век­торами. Для представления синусоидально изменяющейся величины

a=A_msin(wt+¥)

с начальной фазой ¥ вращающимся вектором построим (рис. 2.10, а) радиус-вектор А_m этой величины длиной (в масштабе построения), равной амплитуде А_m, и под углом т|) к горизонтальной оси. Это будет его исходное положение в момент начала отсчета времени t = 0. Из конца радиуса-вектора А_m, находящегося в начальном положении, опустим на горизонтальную ось перпендикуляр, длина которого равна А_msin¥. Предположим, что радиус-вектор вращается с постоянной угловой частотой w = 2п/Т = 2пf против направления движения часовой стрелки, где Т — период, f— частота вращения.






В момент времени t₁ радиус-вектор A_m будет повернут относительно начального положения на угол wt₁ длина перпендикуляра, опущен­ного из его конца, будет равна A_msin(wt₁+¥).

Очевидно, длина перпендикуляра, опущенного из конца вращаю­щегося радиуса-вектора на горизонтальную ось, будет максимальной в момент временя t₂, при котором wt₂+¥=п/2

A_msin(wt₂+¥).= A_msin (п/2) = A_m

Рядом с окружностью, описываемой концом вращающегося радиуса-вектора, можно построить в прямоугольной системе координат график зависимости синусоидальной величины A_msin(wt+¥) от фазы wt или от времени ( (рис. 2.10, б). В момент t₂ синусоидальная величина а достигает максимального значения. Далее по мере вращения радиуса-вектора синусоидальная величина a=A_msin(wt+¥), оставаясь положительной, уменьшается, достигая нулевого значения в момент времени t₄ a в следующие моменты времени, например t₅ и t₆ мгновен­ные значения синусоидальной величины а получаютсяотрицательными, с момента /₇ снова положительными и т. д.

Применение вращающихся векторов позволяет компактно предста­вить на одном рисунке совокупность различных синусоидально изме­няющихся величин одинаковой частоты при анализе сложной электри­ческой цепи.

Представление синусоидальных величин комплексными числами. От представления синусоидальных величин вращающимися ра­диусами-векторами нетрудно перейти к представлению синусоидальных величин комплексными числами.

Дня того чтобы представить заданную в тригонометрической форме синусоидальную величину

а= A_msin(wt+¥) (2.20)

с начальной фазой ¥ комплексным числом, проведем на комплексной. плоскости (рис. 2.11) из начала координат под углом ф к оси действи­тельных величин и чисел вектор, длина которого в масштабе построе­ния равна амплитуде А_тсинусоидальной величины. Конец этого век­тора находится в точке, которой соответствует определенное комплекс­ное число — комплексная амплитуда синусоидальной величины: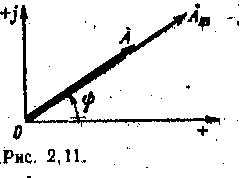




A_m= A_meⁱ¥= A_m <¥

Так же обозначается и соответствующий комплексной амплитуде вектор на комплек­сной плоскости

При увеличении во времени фазы wt+¥ синусоидальной величины угол между век-

тором и осью действительных величин растет, т. е. получается вращающийся вектор

A_meⁱ¥ ^(wt+¥) = A_mcos(wt+¥)+i A_msin(wt+¥)

Нетрудно видеть, что мнимая часть вращающегося вектора равна за­данной синусоидальной величине (2.20).

По существу представление синусоидальной величины комплексной амплитудой Л_т и соответствующим ей вектором на комплексной плос­кости геометрически подобно представлению той же синусоидальной величины вращающимся радиусом-вектором А_m в момент времени t = 0 (рис. 2.10, а). Поэтому может создаться впечатление, что оба представления синусоидальных величин практически совпадают. В дей­ствительности это не так. В случае представления синусоидальных величин комплексными числами можно применить весьма эффективный комплексный метод анализа электрических цепей синусоидального тока, который в настоящее время завоевал всеобщее признание.

Вектор на комплексной плоскости, длина которого в масштабе построения равна действующему значению синусоидальной величины, и соответствующее комплексное число называются комплексным дей­ствующим значением синусоидальной величины:




( 2.21)

Так же обозначается и сам вектор на комплексной (рис. 2.11).

Применяются три формы записи комплексного значения синусои­дальной величины:

показательная форма







тригонометрическая форма






и алгебраическая форма







где А' = Acos¥ и А’’= Asin¥ —действительная и мнимая состав­ляющие комплексного значения синусоидальной величины;
Переход от показательной формы к тригонометрической выполня­ется при помощи формулы Эйлера:




При значениях угла ¥ = п/2 и ¥= —п/2 из формулы Эйлера следуют два часто встречающихся соотношения:







При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных вели­чин; сокращенно их называют комплексными значениями синусоидаль­ных величин, а соответствующие векторы на комплексной плоскости — векторами комплексных значений. Например, синусоидальному току.

соответствует комплексное значение тока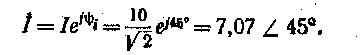



Совокупность векторов комплексных значений синусоидальных величин одной частоты называется векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание комплексных значений можно заменить сложением и вычитанием соответствующих векторов комплексных значений. Это иногда упрощает расчеты и делает их наглядными-

Взаимное расположение векторов комплексных значений на вектор­ной диаграмме не изменится, если начальные фазы ¥ всех комплексных значений уменьшить (увеличить) на одну и ту же величину. Это озна­чает лишь одновременный поворот всех векторов на один и тот же угол. Часто при анализе электрических цепей векторную диаграмму строят так, чтобы вектор одного комплексного значения был направлен вдоль оси действительных величин. Такой вектор комплексного значения назовем исходным вектором.

Направления синусоидальных величин (ток, напряжение и др.), определяющих режим электрической цепи, периодически изменяются, но одно из двух направлений принимается положительным. Это направление выбирается произвольно и показывается стрелкой на схеме соответствующего участка электрической цепи.


При выбранном поло-жительном направлении синусоидальная величина представляется мгновенным значением а = A_msin(wt+¥) и соответствующим комплексным значением А = А<¥ (2.21). Следовательно, взаимно однозначному представлению синусоидальных токов, напряжений и других величин в виде мгновенных и комплексных значений соответствуют их одинаковые положительные направления (рис. 2.12),