электрические и магнитные цепи. 1 электротехнические устройства постоянного тока

• Название: 1 электротехнические устройства постоянного тока
• Анкор: электрические и магнитные цепи.doc
• Дата: 19.08.2018
• Размер: 1.08 Mb.
• Имя файла: электрические и магнитные цепи.doc
• Тип: Документы; #23206
• страница: 6 из 7

ГЛАВА ШЕСТАЯ МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ

6.1. ЭЛЕМЕНТЫ МАГНИТНОЙ ЦЕПИ
Магнитной цепью (магнитопроводом) называется совокупность раз­личных ферромагнитных и неферромагнитных частей электротехниче­ских устройств для создания магнитных полей нужной конфигурации и интенсивности.

В зависимости от принципа действия электротехнического устрой­ства магнитное поле может возбуждаться либо постоянным магнитом, полей катушкой с током, расположенной в той или иной части магнит­ной цепи.

К простейшим магнитным цепям относится тороид из однородного ферромагнитного материала (рис. 6.1). Такие магнитопроводы при­меняются в многообмоточных трансформаторах, магнитных усилите­лях, в элементах ЭВМ и других электротехнических устройствах.

На рис. 6.2 показана более сложная магнитная цепь электромеха­нического устройства, подвижная часть которого втягивается в элект­ромагнит при постоянном (или переменном) токе в катушке. Сила при­тяжения зависит от положения подвижной части магнитопровода.

На рис. 6.3 изображена магнитная цепь, в которой магнитное поле возбуждается постоянным магнитом. Если подвижная катушка, расположенная на ферромагнитном цилиндре, включена в цепь по­стоянного тока, то на нее действует вращающий момент. Поворот катушки с током не влияет на магнитное поле магнитной цепи. Такая

магнитная цепь есть, например, в измерительных приборах магнито­электрической системы.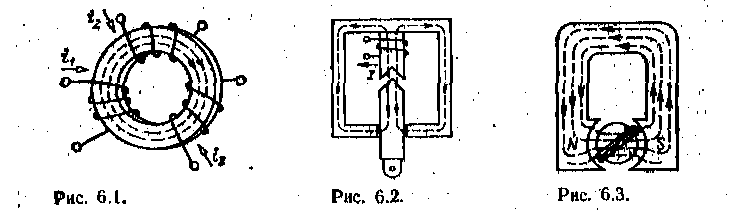




Рассмотренные магнитные цепи, как и другие возможные конст­рукции, можно разделить на не разветвленные магнитные цепи (рис. 6.1 и 6.3), в которых магнитный поток в любом сечении цепи одинаков, и разветвленные магнитные цепи (рис. 6.2), в которых маг-
нитные потоки в различных сечениях цепи различны. В общем случае разветвленные магнитные цепи могут быть сложной конфигурации, например в электрических двигателях, генераторах и других устрой­ствах.

В большинстве случаев магнитную цепь следует считать нелиней--ной, и лишь при определенных допущениях и определенных режимах работы магнитную цепь можно считать линейной.
6.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ЦЕПИ С ПОСТОЯННОЙ МАГНИТОДВИЖУЩЕЙ СИЛОЙ
Закон полного тока получен на основании многочисленных опы­тов. Этот закон устанавливает, что интеграл от напряженности магнитного поля по любому контуру (циркуляция вектора напряжен­ности) равен алгебраической сумме токов, сцепленных с этим контуром:







причем положительными следует считать те токи, направление кото­рых соответствует обходу контура по направлению движения часо­вой стрелки (правило буравчика). В частности, для контура на рис. 6.4 по закону полного тока
Величина I в (6.1) называется магнитодвижуирй силой (сокращенно МДС).

Основной единицей измерения магнитодвижущей силы в системе СИ является ампер ^). Основная единица измерения напряженности магнитного поля в системе СИ — ампер на метр (А/м) — особого наименования не имеет. Часто применяется также единица, кратная •основной единице напряженности магнитного поля, ампер на санти­метр, I А/см = 100 А/м.

Магнитную цепь большинства электротехнических устройств мож) представить состоящей из совокупности участков, в пределах каждо из которых можно считать магнитное поле однородным, т. е. с. постоянной напряжен­ностью, равной напряженности магнитного поля Н/, вдоль средней линии участка длиной I/,. Для таких магнитных цепей можно заменить интегрирование в (6.1) суммированием.

Если при этом магнитное поле возбуж­дается катушкой с током /, у которой ш витков, то для контура магнитной цепи, сцепленного с витками и состоящего из п участков, вместо (6.1) мо> но записать: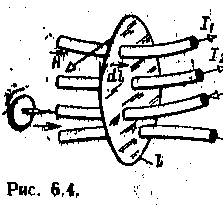










Если контур сцеплен с витками т катушек с токами, то






Таким образом, согласно закону полного тока МДС Р равна сум; произведений напряженностей магнитного поля на длины соотве ствуюшнх участков для контура магнитной цепи. Произведен! #А = ^«6 часто называют магнитным напряжением участка ма нитной цепи.
6.3. СВОЙСТВА ФЕРРОМАГНИТНЫХ МАТЕРИАЛОВ

Магнитное состояние любой точки изотропной среды, т. е. сред с одинаковыми свойствами во всех направлениях, вполне определяете вектором напряженности магнитного поля Н и вектором магнитного. индукции В, которые совпадают друг с другом по направлению.

Основная единица измерения магнитной индукции в системе С называется тесла (Тл); 1. Это нндукщ: такого однородного магнитного поля, в котором магнитный поток ' (см. § 2.3) через поверхность площадью 1 м², перпендикулярна направлению магнитных линий поля, равен одному веберу (Вб),

В вакууме индукция и напряженность магнитного поля связан простым соотношением: В магнип ноя постоянная. Для ферромагнитных материалов зависимость от напряженности магнитного поля В (Н) в общем случае.

Для того чтобы экспериментально исследовать магнитные ферромагнитного материала, необходимо все измерения прои. водить на образце, в котором магнитное поле однородное. Таким « разцом может быть тороид, изготовленный из исследуемого –феррома ннтного материала (рис. 6.5), длина магнитных линий в котором много больше его поперечных размеров (тонкостенный тороид). На тороиде находится равномерно навитая обмотка с числом витков .

Можно считать, что в тороиде из ферромагнитного изотропного материала с плотно намотанными витками все магнитные линии — окружности, а векторы напряженности и индукции магнитного поля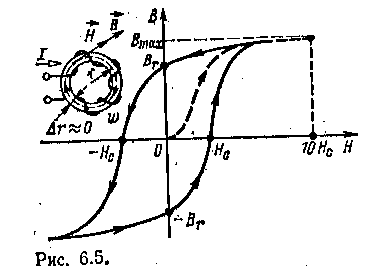






направлены по касательной к со­ответствующей окружности. Так, на рис. 6.5 показана средняя маг­нитная линия и векторы Н и В в одной из ее точек.

При расчете напряженности и индукции магнитного поля в тон­костенном тороиде можно считать, что все магнитные линии имеют одинаковую длину, равную длине средней линии 2лг.

Предположим, что ферромаг­нитный материал тонкостенного тороида полностью размагничен и

Рис. 6.5.


тока / в обмотке пет (В = 0 и Н = 0). Если теперь плавно увеличи­вать постоянный ток / в обмотке катушки, то в ферромагнитном ма­териале возникнет магнитное поле, напряженность которого опре­деляется законом полного тока (6.1):

(6.3>
Каждому значению напряженности Н магнитного поля в тонко­стенном тороиде соответствует определенная намагниченность ферро­магнитного материала, а следовательно, И соответствующее значение

магнитной индукции В.

Если начальное магнитное состояние материала тонкостенного то­роида характеризуется значениями Н = О, В = 0, то при плавном нарастании тока получим нелинейную зависимость. В (Я), которая называется кривой первоначального намагничивания (рис. 6.5, штрихо­вая линия). Начиная с некоторых значений напряженности Я маг­нитного поля индукция В в тонкостенном ферромагнитном тороиде практически перестает увеличиваться и остается равной В_таж. Зга область зависимости В (Я) называется областью технического насыщения.

Если, достигнув насыщения, начать плавно уменьшать постоянный ток в обмотке, т. е. уменьшать напряженность поля (6.3), то индукция также начнет уменьшаться. Однако зависимость В (И) уже не совпадет с кривой первоначального намагничивания. Изменив направление тока в обмотке и увеличивая его значение, получим новый участок зависимости 6 (Я). При значительных отрицательных значениях напряженности магнитного поля снова наступит техническое насыще­ние ферромагнитного материала. Если теперь продолжить экспери­мент: сначала уменьшать ток обратного направления, затем увеличи­вать ток прямого направления до насыщения и т. д., то после несколь-

ких циклов перемагничивания для зависимости В (Н) будет получена симметричная кривая (рис. 6.5, сплошная линия). Этот замкнутый цикл В (Я) называется предельной статической петлей гистерезиса (или предельным статическим циклом гистерезиса) ферромагнитного материала. Если во время симметричного перемагничивания область технического насыщения не достигается, то симметричная кривая В (Я) называется симметричной частной петлей гистерезиса ферромагнит­ного материала.

Предельный статический цикл гистерезиса ферромагнитных ма­териалов характеризуется следующими параметрами (рис. 6.5): Я_с -коэрцитивной силой. В_Г—остаточной индукцией коэффициентом прямоугольности.

По значению параметра Я_с предельного статического цикла гисте­резиса ферромагнитные материалы делятся на группы:

1) магнитные материалы с малыми значениями коэрцитивной силы Я_с<0,05 -т- 0,01 А/м называются магнитно-мягкими;

2) магнитные материалы с большими значениями коэрцитивной силы Я_с > 20 -т- 30 кА/м называются магнитно-твердыми.

Магнитно-твердые материалы используются для изготовления по­стоянных магнитов, а магнитно-мягкие — при изготовлении магни­тол р оводов электротехниче­ских устройств, работающих в режиме перемагничивания по предельному или частным циклам.

Магнитно-мягкие материа­лы в свою очередь делятся на три типа: магнитные материа­лы с прямоугольной предель­ной статической петлей гисте­резиса, у которых коэффициент прямоугольности йгг] > 0,95 (рис. 6.6, с);







магнитные материалы с округлой предельной статической петлей гистерезиса, у которых коэффициент прямоугольности 0,4 < Г — относительная магнитная проницаемость.

Все типы магнитных характеристик ферромагнитных материалов могут быть получены на образцах, изготовленных либо из различных ферромагнитных сплавов, либо из ферромагнитной керамики (фер­риты). Ценное свойство ферритов в отличие от ферромагнитных сплавов — их высокое удельное электрическое сопротивление.

Магнитопроводы из ферромагнитных материалов с прямоугольным предельным статическим циклом гистерезиса применяются в опера­тивной памяти цифровых электронных вычислительных машин, маг­нитных усилителях и других устройствах автоматики. Ферромагнит­ные материалы с округлым предельным статическим циклом гистере­зиса используются при изготовлении магнитопроводов электрических машин и аппаратов. агнитопроводы этих устройств обычно работают

в режиме перемагпичнваипя по симметричным частным циклам. При расчете магнитопроюдов таких электротехнических устройств сим­метричные частные циклы заменяют основной кривой намагничивания ферромагнитного материала, которая представляет собой геометриче­ское место вершин симметричных частных циклов тонкостенного фер­ромагнитного тороида (рис. 6.7), полученных при синусоидальном токе низкой частоты в обмотке.

По основной кривой намагничивания фер­ромагнитного материала определяют зависи­мость абсолютной магнитной проницаемости






от напряженности Я магнитного поля, кото­рая показана на рис. 6.7 пунктиром.

На рис. 6.8 приведены основные кривые намагничивания некоторых электротехниче­ских сталей, используемых в электрических машинах, трансформа­торах и других устройствах, чугуна и пермаллоя.




Из ферромагнитных материалов с линейными свойствами изготов­ляют участки магнитопроводов для катушек индуктивности колеба­тельных контуров с высокой добротностью. Такие контуры применяются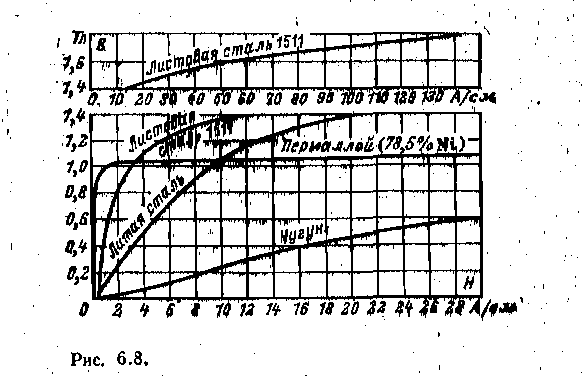




ются в различных радиотехнических устройствах (приемниках, пере­датчиках), в малогабаритных антеннах средств связи и т. д.

Если участок магнитопровода с площадью поперечного сечения 5 нельзя считать тонкостенным, то расчет часто все же можно вести, пользуясь средними значениями индукции В_ср = Ф/S и напряжен­ности H_Ср магнитного поля (на средней магнитной линии). Например, для тороида с прямоугольной формой поперечного сечения, внутрен­ним радиусом г_ь внешним радиусом г_± и высотой \1 изготовленного из

магнитного материала с линейными свойствами, т. е. при В = (см. рис. 6.6,),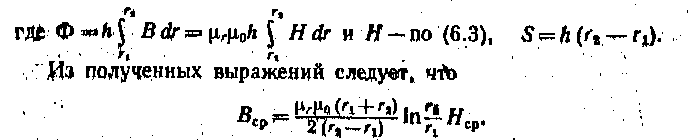














В дальнейшем для упрощения расчетов неоднородность магнит­ного поля в поперечном сечении каждого участка магнитопровода учитывать не будем и будем считать, что поле в каждом участке одно­родное и определяется значениями напряженности и индукции на сред­ней магнитной линии.
6.4. НЕРАЗВЕТВЛЕННАЯ МАГНИТНАЯ ЦЕПЬ
Задачей расчета неразветвленной магнитной цепи в большинстве случаев является определение МДС Р = /да, необходимой для того, чтобы получить заданные значе­ния магнитного потока или маг­нитной индукции в некотором участке магнитопровода (чаще всего в воздушном зазоре).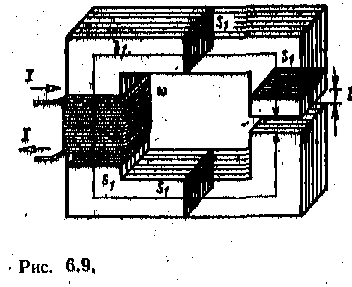






На рис. 6.9 приведен пример не разветвленной магнитной це­пи — магнитопровод постоянно­го поперечного сечения 5! с за­зором. На этом же рисунке ука­заны другие геометрические раз­меры обоих участков магнито­провода: средняя длина маг- Рис. С.9. ннтной линии первого участка из ферромагнитного материала и длина /₂ второго участка — воздуш­ного зазора. Магнитные свойства ферромагнитного материала заданы основной кривой намагничивания В (Я) (рис. 6.10) и тем самым по (6.4) зависимостью \\_а (Я).

По закону полного тока (6.2)




где Н₁ и Н ₂ — напряженности магнитного поля в первом и втором участках.

В воздушном зазоре значения магнитной индукции В_й и напря­женности Я₂ связаны простым соотношением В_г = |1₀Я₂, а для участка из ферромагнитного материала В₁ = ^₀1^1- Кроме того, в неразвет­вленной магнитной цепи магнитный поток одинаков в любом поперечном сечении магнптопровода:






где S_1и S₂ — площади поперечного сечения участка из феррома­гнитного материала и воздушного зазора.

Если задан магнитный поток Ф, то по (6.6) найдем значения индук­ций В_г и В₂. Напряженность поля Н₁ определим по основной кривой намагничивания (рис. 6.10), а Н_а = В₂х._а. Далее по (6.5) вычислим необходимое значение МДС.

Сложнее обратная задача: расчет магнитного потока при задан­ной МДС Р.

Заменив в (6.5) напряженности магнитного поля значениями ин­дукции, получим:







или с учетом (6.6)




магнитное сопротивление участка магнит­ной цепи, причем магнитное сопротивление й-го участка нелинейное, если зависимость В (//) для этого участка нелинейная (рис. 6.10), т.

Для нелинейного магнитного сопротивле­ния г„ можно построить вебер-амперную ха­рактеристику — зависимость магнитного по­тока Ф от магнитного напряжения V '« на со­ответствующем участке магнитопровода. Веберамперная характеристика участка маг­нитопровода рассчитывается по основной кривой намагничивания ферромагнитного материала В (Я). Чтобы по­строить вебер-амперную характеристику, нужно ординаты и абсциссы всех точек основной кривой намагничивания умножить соответственно на площадь поперечного сечения участка 5 и его среднюю длину /,

На рис. 6.11 приведены вебер-амперные характеристики Ф СЛл) для нелинейного магнитного сопротивления г_л (ферромагнитного участка) и Ф ((/_м2) для линейного магнитного сопротивления (воздушного зазора) магнитопровода по рис. 6.9.







Между расчетами нелинейных электрических цепей постоянного тока и магнитных цепей с постоянными МДС нетрудно установить аналогию. Действительно, из уравнения (6.7) следует, что магнитное напряжение на участке магнитной цепи равно произоедению магнит­ного сопротивления участка на магнитный поток. Эта за­висимость аналогична закону Ома для резистивного элемента электрической цепи постоянного тока u = г/(1.1).Сумма магнитных напря­жений в контуре магнитной цепи равна сумме МДС этого контура , что аналогично второму закону Кирхгофа для элек­трических цепей постоянного тока %и = 2Я (1.8).







Продолжая дальше аналогию между электрическими цепями постоянного то­ка и магнитными цепями с постоянными МДС, представим неразветвленную маг­нитную цепь (рис. 6.9) схемой замеще­ния (рис. 6.12, а). Эта схема замещения и схема замещения нелинейной электри­ческой цепи с последовательным соеди­нением элементов (см. рис. 1.31) полно­стью аналогичны (с точностью до обоз­начения параметров элементов). Следовательно, для анализа не-разветвленных магнитных цепей (а также и разветвленных магнит­ных цепей) с постоянной МДС можно пользоваться всеми графиче­скими и аналитическими методами расчета нелинейных электриче­ских цепей постоянного тока (см. § 1.21).

В качестве иллюстрации ограничимся применением для анализа неразветвленной магнитной цепи рис. 6Л2, а графических методов:

метода сложения вебер-амперных характеристик (рис. 6.11) и метода нагрузочной ха­рактеристики (рис. 6.12,6). Согласно первому методу построим вебер-амперную ха­рактеристику всей неразветв­ленной магнитной цепи графически складывая по напряжению вебер-амперные характери­стики ее двух участков. При






известной МДС Р = /да по вебер-амперной характеристике всей маг­нитной цепи определим магнитный поток Ф, а по вебер-амперным характеристикам участков магнитопровода — магнитные напряжения на каждом из них.

Согласно второму методу для второго (линейного) участка построим нагрузочную характеристику (1.39) .




т. е. прямую, проходящую через точку Р на оси абсцисс и точку на оси ординат. Точка пересечения нагрузочной характеристики с вебер-амперной характеристикой ферромагнитного участка цепи Ф (^ш) определяет магнитный поток Ф в цепи и магнитные напряже­ния на ферромагнитном участке И_к1 и воздушном зазоре (У_м2. Значе­ние индукции в воздушном зазоре В_а = Ф/S₄.
6.5. НЕРАЗВЕТВЛЁННАЯ МАГНИТНАЯ ЦЕПЬ С ПОСТОЯННЫМ МАГНИТОМ
Рассмотрим расчет простейшей неразветвленной магнитной цепи с постоянным магнитом. Предположим, что тороид длиной I и пло­щадью поперечного сечения 5 (рис. 6.13, а) изготовлен из магнитно-твердого материала, часть предельного статического цикла гистере­зиса которого В (Я) изображена на рис. 6.13, 6, Материал торолда был предварительно намагничен так, что его магнитное состояние ха­рактеризуется остаточной индукцией В_г.

Вырежем из тороида участок длиной (рис. 6.13, в). Остав­шаяся часть тороида будет-постоянным магнитом, а в образовавшемся воздушном зазоре магнитное поле возбуждается этим постоянным магнитом. Пренебрегая неоднородностью магнитного поля в воздуш-




ном зазоре, будем считать, что всюду в зазоре магнитное поле харак­теризуется напряженностью магнитного поля Я„ и индукцией Учтем, что вследствие «выпучивания» магнитных линий в воз­душном зазоре площадь поперечного сечения воздушного зазора 5_В больше площади поперечного сечения постоянного магнита .

По закону полного тока (6.5) для контура, совпадающего со средней линией магнитопровода,







где Н„ и 1_Я — напряженность магнитного поля и длина средней линии постоянного магнита.

Из (6.8) следует, что






Кроме того, так как магнитный поток Ф в неразветвленной маг­нитной цепи постоянен, то

Подставив значение индукции в воздушном зазоре В_в из (6.10) в (6.9), получим уравнение прямой линии, проходящей через начало координат (рис. 6.13,6):





где— коэффициент размагничивания постоянного магнита.

Точка пересечения прямой „ и предельного статиче­ского цикла гистерезиса материала В (Н) определяет индукцию в маг­ните В = В_н, а следовательно, и индукцию в воздушном зазоре (6.10).

Если в воздушный зазор медленно вводить ферромагнитный за­мыкатель с малым магнитным сопротивлением, то значение индукции в магнитопроводе будет увеличиваться по частному гистерезисному циклу, показанному на рис. 6.13,6 пунктиром. При многократном магнитном замыкании и размыкании воздушного зазора изменение индукции магнита происходит по некоторому установившемуся част­ному циклу.

Для получения больших значений индукции в воздушном зазоре необходимо изготавливать постоянный магнит из магнитно-твердых материалов, т. е. с большим значением коэрцитивной силы Я_с.
6.6, ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА ПОСТОЯННОГО ТОКА
Принцип работы многих электромагнитных устройств постоянного тока, на­пример электроизмерительных приборов, электромеханических реле, электромаг­нитов, основан на электромеханическом дей­ствии магнитного поля. Во всех этих уст­ройствах для.расчета сил, действующих на различные части магнитопроводов. часто -требуется выразить силу через изменение энергии магнитного поля.

В качестве примера рассмотрим опреде­ление силы в системе, состоящей из двух ка­тушек индуктивности; неподвижной с чис­лом ВИТКОВ К>₁ И ПОДВИЖНОЙ С ЧИСЛОМ ВИТ­КОВ а>_г, подключенных к источникам по­стоянного тока ^₁ и У_а (рис. 6.14).




Предположим, что под действием силы притяжения / катушка % перемешается за

время /11 вдоль горизонтальной оси х на расстояние <Их. За время 41 от двух источ­ников постоянного тока в рассматриваемую систему поступит энергия





где р\ и р₂ — мгновенные значения мощности источников; щ. и и₂ — напряжения между выводами катушек.

Будем для упрощения расчетов считать, что потерями в проводах катушек можно пренебречь. В этом случае энергия, полученная от источников тока, расхо­дуется на механическую работу и на изменение энергии магнитного поля системы:





Напряжения «, и щ между выводами катушек возникают вследствие измене-, ния полных по то кос цеп лен и и в каждой из них {см. § 2,22):









Так как в рассматриваемой системе токи в катушках /, и 3₂ и индуктивности катушек ^ и Ь% постоянны, то изменения полных потокосцеплений V] и Т_а вызваны изменением (увеличением) взаимной индуктивности М. (В общем случае изменяться могут и индуктивности катушек вследствие изменения геометрических размеров Последних.) По закону электромагнитной индукции (2.78) напряжения между выводами катушек

В этом уравнении величина в скобках по (2.80) равна удвоенной энергия магнит­ного поля системы 21Р_Ы, откуда Ох. Следовательно, электромеханическая сила, действие которой вызывает перемещение катушки а>_}, может быть найдена через' соответствующее этому перемещению изменение энергии магнитного поля:






Производная положительна, следовательно, электромеханическая сила ! стре­мятся переместить подвижную катушку так, чтобы энергия магнитного поля системы увеличивалась.

Для некоторых устройств можно считать, что при малых перемещениях под­вижного элемента системы потокосцепления практически не изменяются, т. е. в (6. 15)

В таком случае систе­ма не получает энергии от источников и, следовательно,





т. е.¹ перемещение подвижного элемента по направлению действия силы происходит за счет уменьшения энергии магнитного поля, например, в результате уменьшения объема, занимаемого магнитным полем при сохране­нии его интенсивности.

Применим условие (6.17) к конкретно­му случаю— ориентировочному расчету подъ­емной силы электромагнита, в котором маг­нитное поле возбуждается постоянным током катушки (рис. 6.15).





Прежде чем изложить расчет, сделаем небольшое отступление. Вспомним доказан Рис. 6.15.ное в курсе физики положение о том, что магнитное поле постоянного тока в фер­ромагнитной среде с линейными свойствами ц_г = сопз! или в среде без ферромаг-нитиков





называемую удельной энергией магнитного поля. Справедливость (6.18) можно по-казать на частном примере, воспользовавшись (2.5) для катушки с магннтопроводом в виде тонкостенного тора с площадью поперечного сечения 5 и длиной средней магнитной лилии I из ферромагнитного материала с линейными свойствами, т. е. при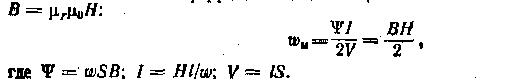






Продолжим теперь расчет подъемной силы электромагнита. Если считать, что индукция В магнитного поля в воздушном зазоре между сердечником и якорем электромагнита не изменяется при перемещении якоря на расстояние дат, то и удель­ная энергия магнитного поля в зазоре остается одной и той же. Следовательно. при перемещении якоря на расстояние А* изменение энергии магнитного поля






Так как было принято, что индукция магнитного поля при перемещении якоря не изменяется, то на основании (6.15) получим;





По этой формуле можно ориентировочно рассчитать подъемную силу электро­магнита любого типа, в котором магнитное поле возбуждается постоянным током катушки. Но при точном расчете необходимо учитывать особенности каждой из кон­струкций.

В общем случае энергия магнитного поля системы зависит не только от взаим­нного расположения ее частей. Поэтому при определении сил, возникающих в маг­нитном поле, следует пользоваться понятием частной производной от эневгии маг­нитного поля по координате перемещения подвижной части, как это сделано в даль­нейшем.