|
|
электрические и магнитные цепи. 1 электротехнические устройства постоянного тока
Uab=rIab или U=rI
1.5. ИСТОЧНИКИ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПОСТОЯННОГО ТОКА
Рассмотрим основные процессы, происходящие в гальваническом элементе, одном из распространенных источников электрической энергии постоянного тока. В простейшем случае гальванический элемент (рис. 1.7, а) представляет собой две пластины — из меди Си н кз цинка 2п, помещенные в раствор серной кислоты Н2ЗО4-»-**• 2Н* +. 5О4-.
Вследствие химических процессов положительные ионы цинка 2п^ переходят в раствор серной кислоты, оставляя на цинковой пластине избыток отрицательных. свободных зарядов. Одновременно в растворе серной кислоты тяжелые и малоподвижные положительные ионы цинка 2пм оттесняют легкие и подвижные положительные ионы водорода ЬГ к медной пластине, на поверхности которой происходит восстановление нейтральных атомов водорода. При этом медная пластина" теряет свободные отрицательные заряды, т, е. заряжается положительно. Между разноименно заряженными пластинами возникает однородное электрическое поле, которое препятствует направленному движению ионов в растворе. Напряжение или разность потенциалов между пластинами аккумуляторной батареи, при которой накопление зарядов прекращается, служит, количественной мерой сторонней силы (в данном случае химической природы), стремящейся к накоплению зарядов.
Количественную меру сторонней силы принято называть электродвижущей силой или сокращенно ЭДС.
Е-в вольтах, если расстояние между пластинами dв метрах; (Qай, = фа -фа напряжение, равное разности потенциалов между выводами пластин в режиме холостого хода.
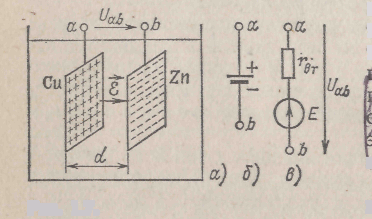
Рис. 1.7
Еслн к выводам гальванического элемента подключить приемник, например резистор, то в замкнутой электрической цепи возникнет ток. Заряд каждой из пластин уменьшится и появится направленное движение ионов в растворе кислоты. Направленное движение ионов сопровождается их взаимными столкновениями, что создает внутреннее сопротивление 'гальванического элемента постоянному току.
Таким образом, гальванический элемент, эскизное изображение которого дано на рис. 1.7, а, а изображение на принципиальных схемах— на рис. 1.7, б, можно представить в виде схемы замещения (рис. 1.7, и), состоящей из последовательно включенных источника ЭДС Е и резистивпого элемента с сопротивлением г„т, равным внутреннему сопротивлению гальванического элемента. Стрелка ЭДС указывает направление движения положительных зарядов внутри источника под действием сторонних сил.
1.6. ИСТОЧНИК ЭДС И ИСТОЧНИК ТОКА
Рассмотрим процессы в простейшей электрической цепи, состоящей из источника электрической энергии, подключенного к резистору. Заменим источник электрической энергии схемой замещения по рис. 1.7, в, а резистор — резистивным элементом с постоянным сопротивлением гя. Схема замещения рассматриваемой электрической цепи представлена на рис. 1.8, а, где буквами аи Ь обозначены выводы источника"электрической энергии.
Свойства источника электрической энергии как элемента схемы замещения можно задать его внешней характеристикой — зависимостью напряжения между его выводами ум = 0 от тока / источника.
Если ЭДС и внутреннее сопротивление источника электрической энергии являются постоянными величинами (линейный источник), то его внешняя характеристика определяется выражением
UаЬ = Фа - Фb = Е — ГвтI, .(1.2)
которому соответствует прямая а-яа рис, 1.9. Уменьшение напряжения между выводами а к Ь источника электрической энергии (рис. 1.8, а) при увеличении тока объясняется увеличением падения напряжения на внутреннем сопротивлении гег источника (увеличением напряжения на резистивном элементе с сопротивлением гвт).
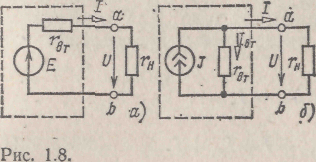
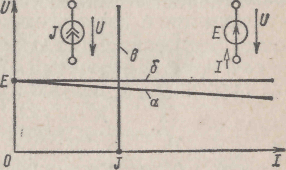
Рис. 1.8 рис. 1.9
Во многих случаях внутреннее сопротивление источника электрической энергии мало по сравнению с сопротивлением гви справедливо неравенство гвт/ <^ Е. В этих случаях напряжение между выводами источника электрической энергии практически не зависит от тока.
Такои идеализированный источник электрической энергии называется идеальным источником ЭДС с одним параметром Е.
Внешняя характеристика идеального источника ЭДС определяется выражением
Уа» = Фа — Фй = Е = СОП5Т, (1.3)
которому соответствует прямая б на рис. 1.9. На этом же рисунке показано изображение идеального источника ЭДС на схемах электрических цепей.
В ряде специальных случаев, в частности во многих цепях с электронными лампами и полупроводниковыми приборами, внутреннее сопротивление источника электрической энергии во много раз больше сопротивления нагрузки ги
При выполнении условия гвт >• ги в таких цепях ток источника электрической энергии
I=El(rвт+rи)
ElrВт=Ik=J
т. е. равен току короткого замыкания источника. Источник электрической энергии с большим внутренним сопротивлением можно заменить идеализированной моделью, у которой г„ •*»• с» и Е *> со и для которой справедливо равенство Е1г„ = ^. Такой идеализированный источник электрической энергии называется идеальным источником тока с одним параметром ^ = 1Х, Ток источника тока не зависит от сопротивления гя внешней цепи. При изменении сопротивления внешней цепи изменяется напряжение между выводами источника Uа!> = г_J
На рис. 1.9 построена прямая в — внешняя характеристика источника тока и дано его изображение на схемах электрических цепей.
От схемы замещения реального источника энергии, представленной в виде последовательного соединения источника ЭДС Е и резистивного элемента о сопротивлением гвт (рис. 1.8, а), можно перейти к схеме замещения с идеальным источником тока. Для этого разделим все слагаемые выражения (1.2) на внутреннее сопротивление источника энергии г„ и получим:
Uablrвт=Elrвт-I
Или
ElrВт=J=UablrВт+I=Iвт+I
Последнее выражение можно истолковать следующим образом: ток источника тока ^ складывается из тока / в резистивном элементе г„ (во внешнем унастке цепи) и тока /вт в резистивном элементе с сопротивлением гвт, включенном между выводами а и Ь источника энергии. Соответствующая эквивалентная схема замещения электрической цепи показана на рис. 1.8, б.
Отметим, что представление реальных источников электрической энергии в виде двух схем замещения является эквивалентным представлением относительно внешнего участка цепи: в обоих случаях одинаковы напряжения между вывода-источника и токи во внешнем участке цепи.
Однако энергетические соотношения в двух схемах замещения реальных источников энергии не одинаковы. Не равны между собой мощности, развиваемые источником ЭДС (рис. 1.8, а) Е1 и источником тока (рис. 1.8, б) 1М, а также мощности потерь, определяемые по закону Джоуля—Ленца:
rВтI2= rВтI2вт
Работа, совершаемая при перемещении положительного ^заряда У вдоль некоторого неразветвленного участка электрической цепи, не содержащего источников электрической энергии, от точки а до точки Ь, равна произведению этого заряда на напряжение иаь = между концами участка: А =QU. При равномерном движении заряда в течение времени /,'т. ег постоянном токе 1аЬ = I, заряд (количество электричества)
Q=It
Следовательно, произведенная за время t работа
A=UIt
Основной единицей работы в системе СИ служит джоуль (Дж), 1 Дж = 1 В-А-с.
Для оценки энергетических условий важно знать, сколь быстро совершается работа. Отношением работы А к соответствующему промежутку времени t определяют мощность
P=Alt=Ul (1.5)
Основной единицей мощности в системе СИ является ватт (Вт), 1 Вт = 1 Дж/с =1 В -А. Это мощность, при которой за одну секунду совершается работа в 1 Дж. Кратные единицы измерения мощности: милливатт (мВт), 1 мВт = 1 • 1(Н Вт; киловатт (кВт), 1 кВт = = ЫО* Вт, и мегаватт (МВт), 1 МВт = ЫО8 Вт=Ы08 кВт.. Основная единица работы и энергии джоуль часто слишком мала для оценки энергетических установок. Практической единицей измерения электрической энергии служит киловатт-час (кВт-ч), т. е. работа, совершаемая при неизменной мощности 1 кВт в течение 1 ч .Так как1Вт-с=1Дж,то1Вт-ч = 3600Вт-с= 3600 Дж и 1 кВт-ч = 3 600 000 Дж.
Для резистивных элементов получается три выражения мощности резиегивного элемента с сопротивлением г в электрический цепи постоянного тока:
Pr=UI=rI2=qU2 (1.6)
В любой электрической цепи должен соблюдаться энергетический баланс — баланс мощностей: алгебраическая сумма мощностей всех источников энергии (в частности источников тока и источников ЭДС или напряжения) равна арифметической сумме мощностей всех приемников энергии (в частности резистивных элементов):
∑UистIист=∑rIr2 или ∑Pист=∑Pr (1.7)
При учете внутренних сопротивлений гвт источников мощность каждого источника Uи„Iн„ меньше развиваемой источником мощности Е1ИСТ на мощность потерь гВТI2ист
Мощность источника следует считать положительной и записывать в уравнении баланса мощностей (1.11) со знаком плюс, если положительное направление тока /„„ совпадает с направлением действия ЭДС. В противном случае эту мощность следует считать отрицательной и записывать со знаком минус (например, для заряжаемого аккумулятора).
1.7 ПРИМЕНЕНИЕ ЗАКОНА ОМА И ЗАКОНОВ КИРХГОФА ДЛЯ РАСЧЕТОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
При помощи закона Ома и двух законов Кирхгофа можно рассчитать режим работы электрической цепи любой сложности.
Общей задачей расчета является определение токов во всех участках цепи при заданных параметрах элементов цепи и известной конфигурации цепи.
Для составления уравнений по закону Ома и двум законам Кирхгофа следует прежде всего выбрать (произвольно) положительные направления токов во всех ветвях рассчитываемой электрической цепи.
При записи уравнений для узлов цепи по первому закону Кирхгофа необходимо иметь в виду, что число независимых уравнений на единицу меньше общего числа узлов у, т. е. нужно составить у — 1 уравнений. Действительно, если составить уравнения для всех у узлов, то ток каждой ветви войдет дважды в уравнения для узлов, так кап ветвь соединяет два узла, причем с противоположными знаками (ток каждой ветви направлен к одному из узлов, и следовательно, направлен от другого узла). При суммировании всех левых частей
уравнений составленных по первому закону Кирхгофа получается тождественно нуль.
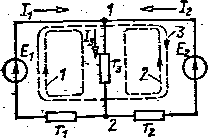
Рис. 1.11
При составлении уравнений на основании второго закона Кирхгофа необходимо также получить независимую систему. В частности, будет получена независимая система, если выбрать контуры так, чтобы каждый следующий содержал хотя бы одну ветвь, не вошед-
шую в контуры, для которых уже составлены уравнения. Такие контуры называются независимыми контурами, так как их уравнения взаимно независимы.
Число неизвестных токов равно числу ветвей в. Для определения этих токов необходимо составить в независимых уравнений. Так как по первому закону Кирхгофа составляется у — 1 независимых уравнений, то на основании второго закона Кирхгофа должно быть составлено в — (у — 1) уравнений.
Например, для цепи по рис. 1.11 можно было бы составить два уравнения на основании первого закона Кирхгофа для двух узлов (выбранные положительные направления токов показаны стрелками). Для узла 1:
I1+I2-I3=0 (1.8)
для узла 2:
I3-I1-I2=0 (1.9)
На основании второго закона Кирхгофа и закона Ома можно было бы составить три уравнения для трех контуров. Для контура 1:
r1I1+r3I3 =E1 (1.10)
для контура 2:
r2I2+r3I3 =E2 (1.11)
для контура 3;
r1I1+r2I2 =E1- E2 (1.12)
Но схема цепи по рис. 1.11 содержит только три ветви, т. е. для ее расчета необходимы три независимых уравнения.
Для этой схемы число узлов у = 2, т. е. по первому закону Кирхгофа должно быть составлено только одно независимое уравнение: (1 8) или (1.9). Действительно, одно из этих уравнений получается из другого умножением на —I.
Из трех контуров на рис. 1.11 независимыми можно, например, считать 1-й и 2-й (во 2-й входит ветвь 2, которую не содержит, 1-й контур). Действительно, уравнение (1.16) можно получить, составив соответственно разности правых и левых частей уравнений (1.10 и (1.11). В качестве независимых для схемы цепи по рис. 1.40 можно взять и любую другую пару контуров.
После совместного решения системы независимых уравнений определяются токи в ветвях цепи. Если для какого-либо тока будет получено отрицательное значение, то из этого следует, что его действительное направление противоположно выбранному положительному направлению.
Совместное решение системы уравнений, составленных на основании двух законов Кирхгофа для сложной цепи, часто требует значительной затраты времени. Поэтому желательно, когда это возможно, вести расчеты более простыми методами, которые рассматриваются в следующих параграфах. Все эти методы основываются на законах Ома и Кирхгофа.
Вряде случаев расчет сложной электрической цепи существенно упрощается, если в этой цепи заменить группу резистивиых элементов другой эквивалентной группой, в которой резистивные элементы соединены иначе, чем в заданной цепи. Взаимная эквивалентность двух групп резистивных элементов определяется тем, что после замены режим работы остальной части электрической цепи не изменится.
В общем случае цепь из резистивных элементов по схеме n-лучевая звезда может быть замещена эквивалентной цепью по схеме n -сторонний многоугольник. В обратном направлении преобразование возможно в ограниченном числе случаев. В частности, преобразования в обоих направлениях возможны для цепей резистивных элементов по схемам треугольник и трехлучевая звезда. Такое преобразование часто применяется для сложных цепей постоянного тока, но особенно важно при расчетах сложных цепей трехфазного тока (гл. 3).
Условия эквивалентности цепей по схемам треугольник и звезда (рис. 1.12) проще всего определяются приравниванием значений сопротивлений и проводимостей между одноименными узлами этих.
Чтобы определить сопротивление ветви по схеме звезда rа найдем:
ra=rAB rCAI ∑r ∆ (1.13)
Два другие выражения для определения сопротивлений ветвей цепи по схеме звезда получим путем простой циклической перестановки индексов:
rB=rBC rABI ∑r ∆ (1.14)
rC=rCA rBCI ∑r ∆ (1.15)
Определим сопротивление ветви эквивалентной цени по схеме треугольник:
rAB=rA+ rB + rA rB /rC (1.16)
Посредством циклической перестановки индексов в (1.24) найдем выражения для сопротивлений двух других ветвей
rBC=rB+ rC + rB rC /rA (1.17)
rCA=rC+ rA + rC rA /rB (1.18)
1.8 МЕТОД ДВУХ УЗЛОВ
Часто исследуемая электрическая цепь содержит только два узла или легко может быть преобразована в подобную цепь. Наиболее простым методом расчета вэтом случае является метод двух узлов (узлового напряжения).
На рис. 1.10 показана схема цепи с двумя узлами а и Ь, состоящая пветвей.
Так как ветви между узлами а и & соединены параллельно, то разность потенциалов или напряжение между этими узлами можно выразить через ЭДС ЕК, ток /е и сопротивление резистивного элемента /> любой из ветвей. По обобщенному закону Ома .
IR=(Uba+ER)/rR=( ER - Uba) /rR
откуда
Uba=фа-фb= ER- rR IR
где Uba — узловое напряжение цепи.
На основании этих соотношений ток
IR=(ER - Uba) qR (1.19)
где qR = 1 /rR — проводимость R-й ветви.
В схеме цепи (рис. 1.19) было принято, что все ЭДС направлены к одному из узлов цепи (к узлу а) и положительное направление каждого тока совпадает с направлением ЭДС в ветви, т. е. все токи направлены к тому же узлу. В действительности, конечно, некоторые ЭДС могут быть направлены к узлу Ь. В этом случае при расчете токов в ветвях с теми же положительными направлениями (к узлу о) по (1.19) значения ЭДС, действующих к узлу Ъ, должны быть записаны со знаком минус.
По первому закону Кирхгофа алгебраическая сумма токов в узле цепи равна нулю, т. е.
I1+I2 +…+IR+…+ In=∑nR=1 IR=0
и, следовательно,
∑nR=1 (ER - Uba) qR=0,
откуда узловое напряжение определяется через параметры элементов цепи:
рис 1.13
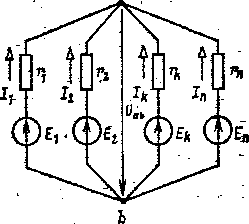
Uba=∑nR=1 ERqR/∑nR=1 qn (1.20)
здесь со знаком плюс записываются ЭДС, действующие к узлу а.
Зная напряжение между узлами, по (1.19) легко определить ток в любой ветви.
1.9 МЕТОД КОНТУРНЫХ ТОКОВ
Этот метод может быть применен для расчета любой линейной ш?пи. Его применение позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Кирхгофа.
Для расчета методом контурных токов в сложной электрической Цепи (рис. 1.14 а) независимые контуры выбираются так же как и при составлении уравнений по второму закону Кирхгофа, например контуры-ячейки (рис. 114 б). Затем в каждом из контуров произвольно выбирается положительное направление контурного тока(один и тот же ток во всех ветвях соответствующего контура). Расчетную величину — контурный ток обозначим по номеру контура с двойным индексом, например IRR. Токи в общих для двух или более контуров ветвях определяются на основании первого закона Кирхгофа как алгебраические суммы соответствующих контурных токов.
Алгебраическая сумма ЭДС всех ветвей, входящих в каждый из выбранных независимых контуров, называется контурной ЭДС еьь (с двойным индексом номера контура), т. е. для любого R-го контура
ЕRR = ∑Е. (1.21)
В выражении (1.21) все ЭДС ветвей, направление которых совпадает (не совпадает) с направлением обхода контура, записываются со знаком плюс (минус).
Арифметическая сумма сопротивлений всех резистивных элементов, входящих в каждый из выбранных контуров, называется собственным контурным сопротивлением rRR, (с двойным индексом контура), т. е.
rRR=∑r (1.22)
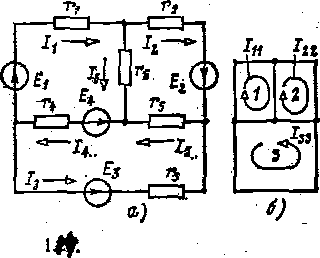
Рис 1.14
Арифметическая сумма сопротивлений резистивных элементов, находящихся в общих ветвях двух контуров т и I, называется общим сопротивлением этих контуров, причем, очевидно,
rml= rlm
Для контурных токов, как и для токов в ветвях, должен выполняться второй закон Кирхгофа. Поэтому составим систему контурных уравнений для контурных токов по второму закону Кирхгофа для электрической цепи, у которой п независимых контуров:
r11I11+ r12I12 +…+ r1nInn =E11
r21I11+ r22I22 +…+ r2nInn =E22
…………………………… (1.20)
rn1I11+ rn2I12 +…+ rnnInn =Enn
Система уравнений (1.23) является математической формулировкой метода контурных токов. Так как число контурных токов (рис, 1.14 б) всегда меньше числа токов в ветвях (рис. 1.14а), то применение метода контурных токов уменьшает число неизвестных величин в решаемой системе уравнений, что весьма существенно при анализе сложных электрических цепей.
Решение системы уравнений (1.23)может быть записано для контурных токов в общей форме с введением определителей:
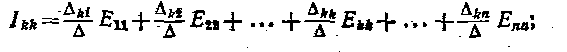 (1.24) (1.24)
здесь определитель системы уравнений
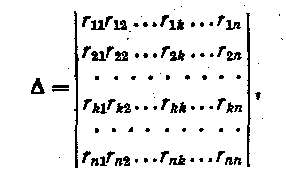
(1.25)
а АRp (р = 1,2, .„, п) —алгебраические дополнения, получаемые из определителя Д посредством вычеркивания R-й строки и р-го столбца" и умножения полученного определителя на (—1)R+р.
Метод контурных токов можно применить и для расчета режима цепи в том случае, если ее схема содержит не только источники ЭДС, но и источники тока. В этом случае ток каждого контура, который содержит источник тока, известен и равен току источника. Поэтому для таких контуров составлять уравнения в системе (1.82) не нужно. Уравнения составляются для всех остальных независимых контуров.
Вторым универсальным методом расчета сложных электрических цепей с любым числом узлов является метод узловых потенциалов (называемый также методом узловых напряжений). Для цепей с двумя узлами этот метод был рассмотрен.
1.10 ПРИНЦИП И МЕТОД НАЛОЖЕНИЯ (СУПЕРПОЗИЦИИ)
Для линейных электрических цепей постоянного тока с' источниками ЭДС, тока и резистивными элементами согласно принципу наложения ток в любой ветви равен алгебраической сумме токов в этой ветви (частичных токов) при действии каждого источника в отдельности, остальные источники заменяются резистивными элементами с сопротивлениями, равными внутренним сопротивлениям соответствующих источников"*1.
Для самых различных расчетов линейных цепей часто применяется метод наложения(суперпозиции), который может быть применен ко всем электрическим процессам, описываемым линейными уравнениями.
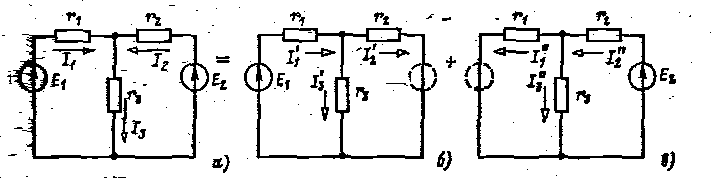
Рис 1.15
На рис. 1.15а, и показана последовательность расчета с применением метода наложения электрической цепи, содержащей источники ЗДС в двух ветвях.
После исключения ЭДС Егполучается простое смешанное соединение резистивных элементов (рис. 1.15б). Ток в неразветвленной части.
токи в двух параллельных ветвях
Затем исключается ЭДС Е1 (рис. 1.15, в) и аналогично рассчитываются токи I2II, I1II и I3II
По методу наложения токи в ветвях электрической цепи рис. 1.15 а
I1=II1- III1; I2=II2- III2; I3=II3- III3;
Существенным недостатком метода наложения является необходимость повышенной точности расчета в том случае, когда частичные токи имеют противоположное направление и близки по значениям. Повышенная точность необходима из-за того, что относительно небольшая погрешность при расчете частичного тока может привести к большой погрешности в окончательном результате.
1.11 МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА (АКТИВНОГО ДВУХПОЛЮСНИКА)
Этот метод целесообразно применять в тех случаях, когда нужно рассчитать ток только в одной ветви аЬ сложной электрической цепи, например в приемнике, подключенном к выходу усилителя. Подобного рода задача часто встречается также при расчетах устройств для электрических измерений неэлектрических величин, систем автоматического регулирования и т. п.
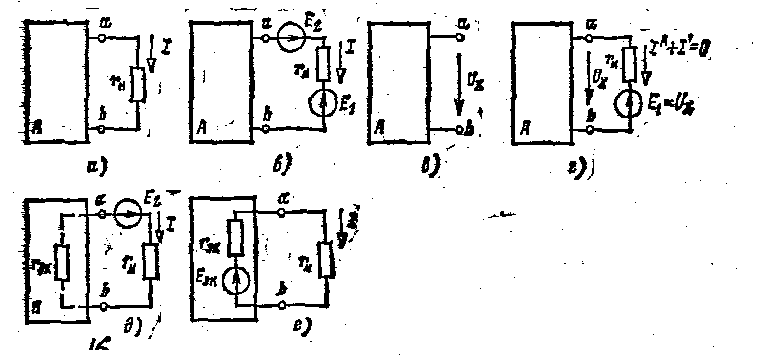
Рис 1.16
Будем считать ветвь аЬ внешней по отношению ко всей остальной части электрической цепи, которая может содержать источники ЭДС, источники тока и резистивные элементы с постоянными сопротивлениями. Эту часть цепи можно рассматривать как активный двухполюсник по отношению к ветви аЬ, с которой она соединяется двумя выводами (полюсами) а и & (рис. 1.16 а). На этом рисунке активный двухполюсник условно изображен в виде прямоугольника с буквой А (активный) и показаны два его вывода а и Ь. Двухполюсник, который не содержит источников энергии, называется пассивным двухполюсником и изображается прямоугольником с буквой П (пассивный).
Сравнив схемы на рис. 1.16 а и д, заключаем, что для активного двухполюсника можно составить эквивалентную схему замещения с ЭДС Евк = Е2 = Uх и внутренним сопротивлением гяк = гвх т. е. заменить его эквивалентным генератором (рис. 1-4Ке).
Для электрической цепи с эквивалентным генератором .
I=Eэк/(rи+rэк)=Ux/( rи+rвх) (1.26)
Выражение (1.8Й) показывает, что для определения токз в приемнике достаточно знать два параметра активного двухполюсника: напряжение холостого хода между его выводами и входное сопротивление, которое можно измерить при помощи соответствующих приборов. Знание электрической цепи активного двухполюсника при этом, не обязательно.
Для определения параметров активного двухполюсника часто пользуются методом холостого хода и короткого замыкания. Измерив при помощи вольтметра напряжение холостого хода между выводами двухполюсника Ux, а затем при короткозамкнутых выводах а и b (ги = 0 ) ток короткого замыкания при помощи амперметра, непосредственно из (1.26) можно определить входное сопротивление гик = Uк/Iк.
1.12 ПЕРЕДАЧИ МАКСИМАЛЬНОЙ МОЩНОСТИ ПРИЕМНИКУ
В устройствах связи, в электронике, автоматике и т. д. очень часто желательно передать от источника к приемнику (исполнительному механизму) наибольшую возможную в данных условиях анергию, причем КПД передачи имеет второстепенное значение.
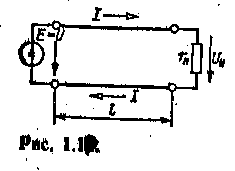
В качестве простого примера такой передачи рассмотрим питание наемника с сопротивлением ги от источника энергии с ЭДС Е и внутренним сопротивлением гвт находящегося на некотором расстояний приемника и соединенного с приемником двухпроводной линией с общим сопротивлением проводов ги (рис. 1.17)
Обозначим сумму внутреннего сопротивления гвт источника энергии исопротивления проводов гпчерез г, т. е. г = гп + гвт. По закону Ома ток в рассматриваемой цепи I= Е/(г +га) и мощность приемника.
(по закону Джоуля — Ленца)
Pи=rиI2= гиE2/(r+rи)2
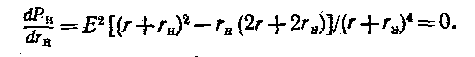
При двух предельных значениях сопротивления гн = 0 и гн = мощность приемника равна нулю, так как в первом случае равно нулк напряжение между выводами приемника, а во втором случае — ток в цепи. Следовательно, некоторому определенному значению гв соответствует наибольшее возможное {при данных Е и г) значение мощности приемника. Чтобы определить это значение сопротивления гц, приравняем нулю первую производную от мощности Ра по ги:
Так как знаменатель этого выражения не равен бесконечности, то
(r+rи)2-2rиr-2rи2=0
Откуда следует, что мощность приемника будет максимальна при условии
rи=r (1.27)
Эта максимальная мощность
Риmax=r(E/2r)2=E2/4r (1/28)
Равенство (1.27) называется условием максимальной мощности приемника.
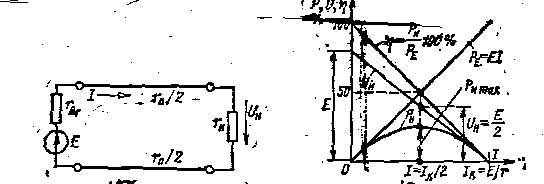
Рис 1.17 Рис 1.18
На рис. 1,18 показаны зависимости от тока мощности приемника Ри= r I2мощности ре= (гн + г) I2 = EI, развиваемой источником энергии, напряжения приемника Uаи КПД передачи энергии.
n= Ри/ Рe
После подстановки значений Ри и Рe для КПД получим зависимость от сопротивления приемника:
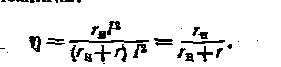
(1.29)
В режиме максимальной мощности (г„ = т) КПД т] = 0,5, т е. половину мощности, развиваемой источником, составляет мощность потерь на внутреннем сопротивлении источника и в передающей системе.
Такой низкий КПД совершенно неприемлем для электроэнергетических систем, где потери энергии при передаче не превышают примерно 10 % энергии, вырабатываемой источниками.
В устройствах электросвязи, автоматики и т. п. мощность приемников энергии невелика. Она составляет часто милливатты; поэтому с энергетической точки зрения допустимы передачи с относительно малыми КПД. Важно, чтобы как можно большая доля мощности источника была использована в исполнительном устройстве (например, в телефонной трубке). По указанной причине режим максимальной мощности широко используется в соответствующих отраслях электротехники.
Здесь было определено условие получения максимума мощности 1 приемнике для простой цепи с линией передачи. Но полученное условие имеет более широкое значение. Достаточно вспомнить, что сколь угодно сложную линейную цепь, содержащую источники энергии и соединенную с приемником при помощи двух выводов, можно заменить ^эквивалентным генератором с ЭДС ЕэК и внутренним сопротивлением Е К такому эквивалентному генератору, замещающему любой активный линейный двухполюсник, применимо условие максимальной мощности. При подключений к выводам активного двухполюсника приемника с сопротивлением га = г№ мощность приемника будет максимальна.
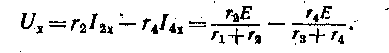
В этом режиме токи I2х = Е/(г1 + г2) и I4x = = Е/(г3 +г4), напряжение
Входное сопротивление двухполюсника относительно выводов а и Ь •(источник ЭДС Е не действует и точки сии короткозамкнуты, т. е. параллельно соединены резистивные элементы с сопротивлениями г1, г2 и гэ, г4:
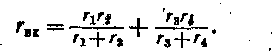
Ток в диагонали четырехплечего моста по (1.37)
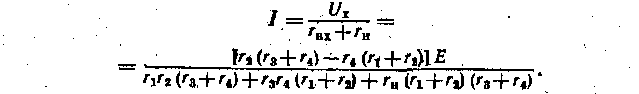
Если сопротивления резистивных элементов трех плеч моста н ЭДС источника неизменны, то изменение тока в диагонали моста будет зависеть только от изменения значения сопротивления резистивного элемента одного плеча. В случае резистивного элемента, сопротивление которого зависит от параметров внешней среды (температуры, давления, влажности и т. д.), изменение тока в диагонали моста будет в некотором масштабе отражать изменения этих параметров. Такой четырехплечий мост может служить преобразователем для измерения неэлектрических величин.
В устройствах регулирования четырехплечий мост применяется в цепях обратной связи. Значение и направление тока в диагонали моста являются исходной информацией для изменения положения рабочих органов регулирующей аппаратуры так, чтобы значение регулируемого параметра было номинальным в состоянии покоя, когда тока в диагонали моста нет.
1.13 НЕЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
В общем случае у всех электротехнических устройств постоянного тока зависимость тока от напряжения между выводами устройства нелинейная: I(U). Если эта нелинейность в широком диапазоне изменений значений тока н напряжения невелика, то при расчетах можно такое электротехническое устройство представить линейной схемой замещения.
Практически, однако, встречается значительное число электротехнических устройств, у которых зависимости I(U) существенно нелинейные .
На рис. 1.19 приведены в качестве примера нелинейные характеристики I(U) трех электротехнических устройств при постоянном токе: и— лампы накаливания; б — полупроводникового диода; в — электронной лампы. Сравнение этих внешних характеристик показывает, что существует большое их разнообразие.
Для расчета электрических цепей с нелинейными электротехническими устройствами последние ' необходимо представить в виде нелинейных схем замещения. В простейшем случае элементами нелинейной схемы замещения являются нелинейные резистивные элементы. На рис. 1.20 приведено условное изображение нелинейного резистивного элемента, который в цепи постоянного тока представляет схему замещения каждого из электротехнических устройств, характеристики которых даны на рис. 1.19
Характеристика I(U) определяющая свойства нелинейного резистивного элемента, называется вольт-амперной характеристикой(сокращенно ВАХ); она может быть задана аналитически, графически (рис. 1.19) или в виде таблицы.
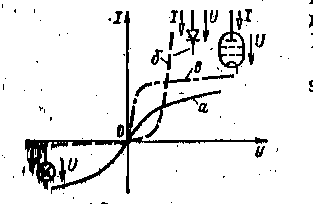
В общем случае нелинейные схемы Замещения электротехнических устройств
Рис 1.19 Рис 1.20
постоянного тока содержат кроме нелинейных резистивных элементов еще и нелинейные источники напряжения и тока, нелинейные свойства которых также задаются их внешними (вольт-амперными) характеристиками.
В дальнейшем ограничимся анализом нелинейных электрических цепей, содержащих только нелинейные резистивные элементы.
Вследствие нелинейности вольт-амперных характеристик I(U) нелинейных резистивных элементов для расчета нелинейных электрических цепей нельзя применять метод наложения. Метод контурных токов, метод узлового напряжения, метод преобразования. Метод эквивалентного генератора можно применить для расчета нелинейной электрической цепи при условии, что активный двухполюсник не содержит нелинейных резистивных элементов. При графическом методе расчета последовательность операций сохраняется примерно той же, что и при расчетах линейных цепей, только вместо сложения или вычитания значений напряжений или токов производится сложение или вычитание абсцисс или ординат соответствующих вольт-амперных характеристик.
Рассмотрим особенности применения графического метода для анализа электрических цепей с последовательным, параллельным и смешанным соединениями нелинейных резисторов.
Последовательное соединение нелинейных резистивных элементов. На рис. 1.Задана схема электрической цепи, содержащая два последовательно соединенных нелинейных резистивных элемента, и построены их вольт-амперные характеристики I(U1) и I (И2).
Если к такой электрической цепи подключить источник тока, то анализ цепи становится тривиальным. Действительно, при известном токе источника, т. е. и в. нелинейных резистивных элементах, напряжения на элементах можно определить непосредственно повольт-амперным характеристикам.
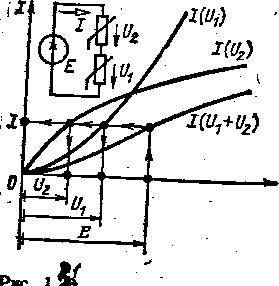
Рис 1.21 Рис 1.22
Анализ цепи сложнее, если к электрической цепи подключен источник ЭДС Е. В этом случае для расчета режима нелинейных резистивных элементов необходимо выполнить эквивалентное преобразование цепи.
Заменим схему цепи с двумя последовательно включенными нелинейными резистивными элементами схемой с одним эквивалентным нелинейным резистивным элементом. Так как значения токов в преобразуемых и эквивалентном нелинейных резистивных элементах должны быть одинаковыми, то вольт-амперная характеристика эквивалентного нелинейного резистивного элемента строится графическим суммированием по напряжению вольт-амперных характеристик I(U1) и I(U2) как и показано на рис. 1.21.
По вольт-амперной характеристике эквивалентного резистивного элемента при известном значении ЭДС Е источника сразу графически определяется ток в цепи/. Для найденного тока по вольт-амперным характеристикам нелинейных резистивных элементов I(U1) и I(U2) легко найти и значения напряжений U1 и U2.
Если электрическая цепь содержит не два, а большее число последовательно соединенных нелинейных резистивных элементов с известными вольт-амперными характеристиками, то анализ цепи выполняется аналогично.
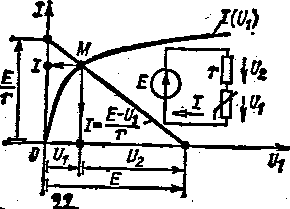
На практике часто встречаются электрические цепи, содержащие последовательное соединение нелинейного и линейного резисторов, например в различных типах усилителей, в которых роль нелинейного элемента выполняет транзистор или какой-либо другой прибор. Анализ таких цепей целесообразно выполнять графическим методом нагрузочной характеристики. Для расчета режима анализируемой цепи (рис. 1.22) запишем уравнение по второму закону Кирхгофа:
rI+U1=E
откуда I=(E-U1)/r (1.30)
При постоянных значениях Е и r из (1.39) следует, что между током I в линейном резистивном элементе и напряжением U1 на нелинейном резистивном элементе существует линейная зависимость I=F(U1) которая называется нагрузочной характеристикой (это внешняя характеристика активного двухполюсника относительно выводов нелинейного элемента).
Построим нагрузочную характеристику — прямую (рис. 1 .31), которая должна проходить через две точки соответственно на оси абсцисс и ординат: из (1.30) при I = 0 находим U1= Е и при U1 = 0 ток I = Е/г.
Ток во всех элементах при последовательном соединении имеет одинаковое значение, которое должно удовлетворять как нагрузочной характеристике I=F(U1), так и вольт-амперной характеристике нелинейного резистивного элемента / ({Д). Следовательно, точка пересечения этих характеристик (точка М на рис. 1.22) определяет режим цепи, т. е. значения тока I и напряжений U1и U2.
Параллельное соединение нелинейных резистивных элементов. На рис. 1.23 дана схема электрической цепи, состоящей из двух нелинейных резистивных элементов, соединенных параллельно. Подключение к такой цепи источника ЭДС приводит к тривиальной задаче. При заданном напряжении ток в каждом из нелинейных резистивных элементов определяется непосредственно по вольт-амперным характеристикам I1(U) и I2(U). Если к цепи, состоящей из параллельного соединения нелинейных резистивных элементов, подключить источник тока J (рис. 1.2З). то анализ цепи можно выполнить графическим методом. Для этого заменим два нелинейных резистивпых элемента, соединенных параллельно, одним эквивалентным нелинейным резистивным элементом. Так как значения напряжений на преобразуемых и эквивалентном нелинейных резистивных элементах должны быть одинаковыми, то вольт-амперная характеристика эквивалентного нелинейного резистивного элемента строится графическим суммированием по току вольт-амперных характеристик I1(U) и I2(U).
При известном токе J источника по характеристике эквивалентно нелинейного резистивного элемента сразу определяется значение приложенного к нему напряжения U, которое равно напряжению на каждом из нелинейных резистивных элементов, соединенных параллельно. По вольт-амперным характеристикам I1(U) и I2(U) определяются токи I1 и I2 в нелинейных резистивных элементах (рис 1.23)
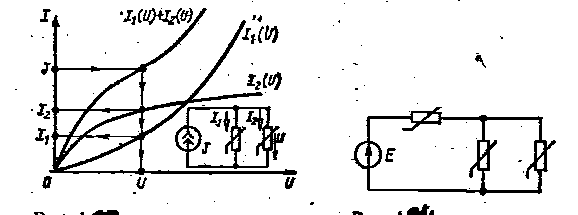
Рис 1.23 Рис 1.24
Если электрическая цепь содержит не два, а большее число параллельно соединенных нелинейных резистивных элементов с известными вольт-амперными характеристиками, то анализ цепи выполняется аналогично.
Анализ цепи со смешанным соединением нелинейных резистивных элементов и одним источником энергии (рис. 1.24) не содержит ничего принципиально нового. При применении графического метода сначала -параллельное соединение нелинейных резистивных элементов заменяется эквивалентным нелинейным резистивным элементом, как было показано выше. После такого преобразования схема электрической цепи содержит два нелинейных резистивных элемента, соединенных последовательно. Анализ такой цепи также рассмотрен выше.
Графические методы расчета нелинейных электрических цепей очень наглядны, но достаточно трудоемки.
|
|
|
 Скачать 1.08 Mb.
Скачать 1.08 Mb.